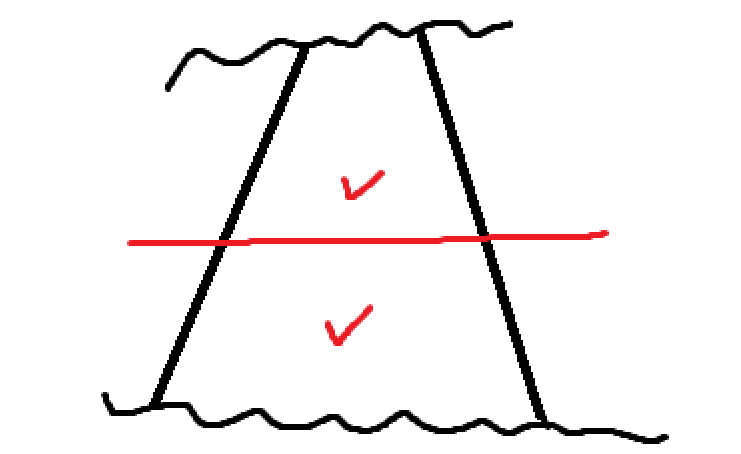
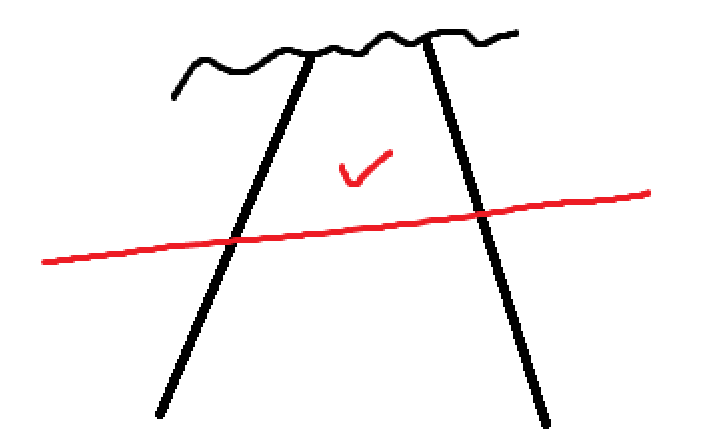
注:本节内容为《具体数学》(原书第二版) 第一章 递归问题 热身题答案。
写在前面
有的时候解决习题的最大难点是理解题意。
1.3
题意:每一种“能够成立的叠放”都会被遇到。
答案:
所有“能够成立的叠放”一共只有 $3^n$ 种,因为每个圆盘都有可能在 3 个圆柱上的任意一个,且一旦所有圆盘都确定了所在的柱子,排列方式只有一个,所以共有 $3^n$ 种。
根据 1.2 问的结论,由于最少使用 $3^n-1$ 次移动才能达成目标,所以最少会经历 $3^n-1+1 = 3^n$ 种不同的状态,所以每种可行的状态都会被遇到。注意:
- 为什么会 +1?因为有初始状态
- 为什么这样是最少的?假设这样不是最少的,即某一种情况可能经历了两次,那么问题来了,为什么在第一次遇到那种情况的时候不直接执行第二次遇到那种情况后的步骤,第一次遇到到第二次遇到中间的步骤都是冗余。
1.4
证明:数学归纳法。省略初值证明。假设 $n$ 的情况成立,最多只需移动 $2^n - 1$ 次。
(一)若最大的圆盘移动
对于 $n + 1$ 的情况:
- 前 $n$ 个圆盘移动到某个塔上,次数 $\leq 2 ^ n - 1$
- 将 $n + 1$ 个圆盘移动到目标塔,次数 $1$
- 将 $n$ 个圆盘移动到目标塔,次数 $\leq 2^n - 1$
故总次数 $\leq 2 * 2 ^ n - 2 + 1 = 2 ^ {n + 1} - 1$
(二)若最大的圆盘不移动
对于 $n + 1$ 的情况:只需要考虑前 $n$ 个圆盘
故总次数 $\leq 2 ^ n - 1 \leq 2 ^ {n + 1} - 1$
1.5
答案:不可能
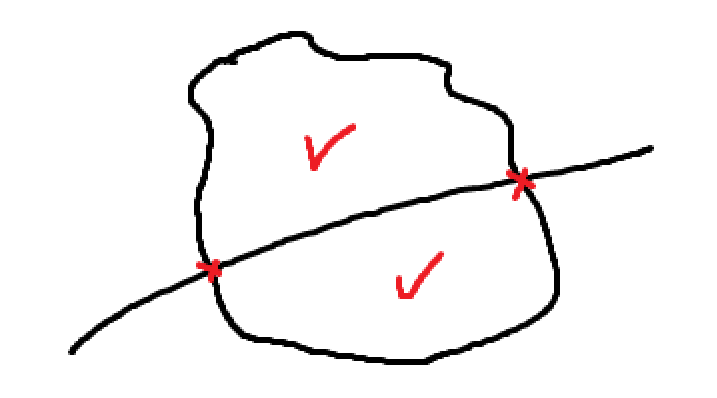
两个圆至多产生 2 个交点。对于 3 个圆,目前的状态共有 6 个圆。
第四个圆最多增加 6 个交点,变为 $6 + 2 * 3 = 12$ 个交点。增加 6 个交点最多增加 6 个区域,区域总数最多为 14 个,不足 16,故不可能。
求证:增加 6 个交点最多增加 6 个区域
证明:
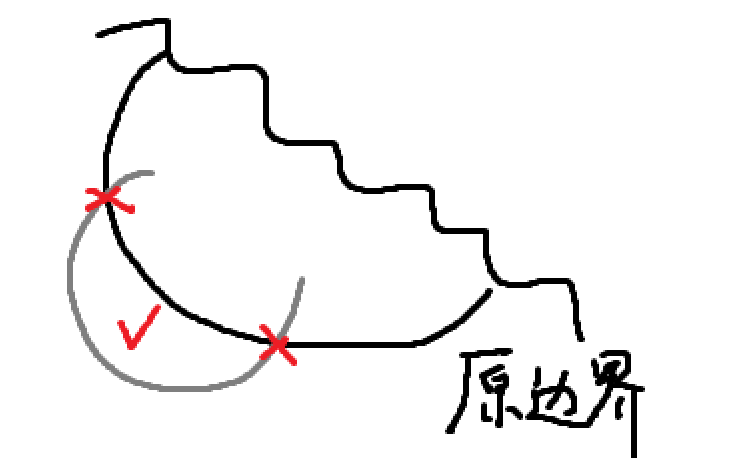
对于连续的两个交点,至多增加一个区域,增加区域有两种情况:
- 分割原图形种的闭合区域
- 增加新的区域
两个连续的交点也可能不增加区域,情况如下:
- 连续相切点
- 新区域的构造超过了两个点
1.6
$$
1 + 2 + \cdots + (n - 1) = \frac 1 2 (n - 1) (n - 2)
$$
下面证明上界(即至多)
引理 1:构成一个必和图形至少需要三条边,故只有在 $n \geq 3$ 时才能有第一个闭合图形
求证:对于平面上已有 $n$ 条直线的情况,第 $n + 1$ 条直线至多产生 $n - 1$ 个闭合图形。
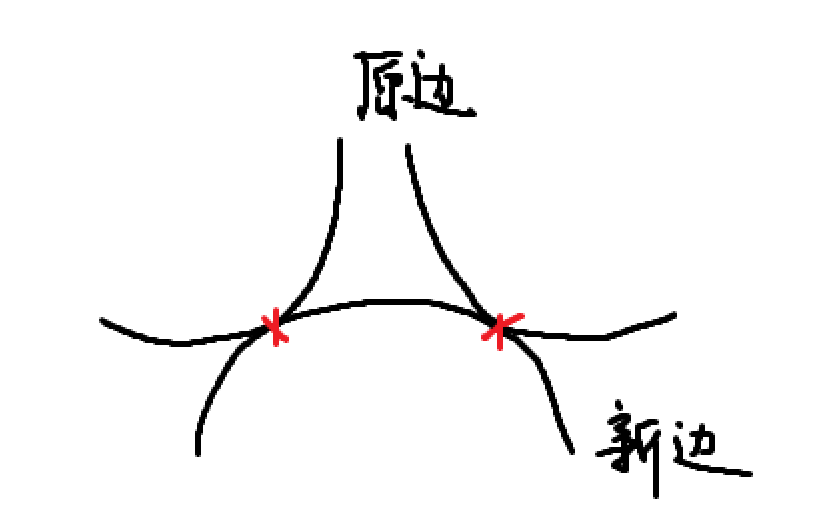
证明:因为产生新闭合图形只有两种情况:
- 分割已有图形
- 增加新区域
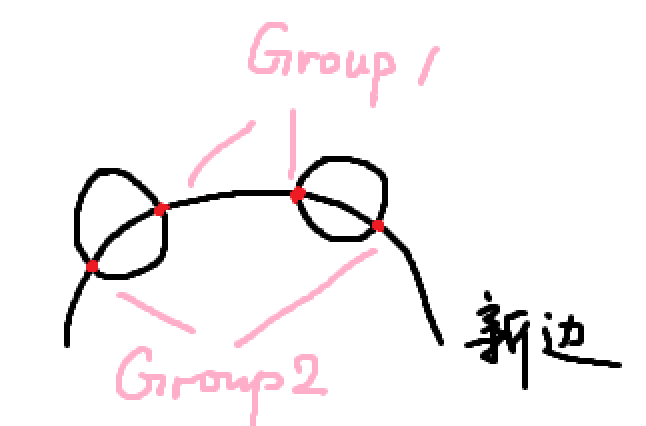
而上述两种情况都需要贡献两个连续的交点。第 $n + 1$ 条直线与已有的 $n$ 条直线至多产生 $n$ 个交点,故最多产生 $n - 1$ 组连续交点,最多增加 $n - 1$ 个闭合区域。
下面证明下界(即至少)
我们可以采用 1.2 节给出的构造,就能够得到 $\frac 1 2 (n - 1) (n - 2)$。
Q.E.D.