注:本节内容为《具体数学》(原书第二版) 第一章 递归问题 作业题答案。
1.9
1.9a
令 $x_n = (x_1 + \cdots + x_{n-1}) / (n-1), (n > 1)$。下略。
1.9b
本小题做法和答案不同。
令
$$
y_1 = x_1 + x_2 + \cdots + x_n, x_i \geq 0
$$
$$
y_2 = x_{n+1} + x_{n+2} + \cdots + x_{2n}, x_i \geq 0
$$
$$
\begin{aligned}
& (y_1 y_2) ^ n \leq \Big ( \frac {y_1 + y_2} 2 \Big) ^ {2n} \\
\Leftrightarrow & \frac {(y_1 y_2) ^ n} {n ^ {2n}} \leq \frac 1 {n ^ {2n}} \Big ( \frac {y_1 + y_2} 2 \Big) ^ {2n} = \Big ( \frac {y_1 + y_2} {2n} \Big) ^ {2n} \\
\Leftrightarrow & \frac {(y_1 y_2) ^ n} {n ^ {2n}} \leq \Big ( \frac {x_1 + x_2 + \cdots + x_{2n}} {2n} \Big) ^ {2n} \\
\Leftrightarrow & \Big (\frac {y_1} n \Big ) ^ n \Big (\frac {y_2} n \Big ) ^ n \leq \Big ( \frac {x_1 + x_2 + \cdots + x_{2n}} {2n} \Big) ^ {2n} \\
\Leftrightarrow & \boxed{\Big (\frac {x_1 + \cdots + x_n} n \Big ) ^ n \Big (\frac {x_{n+1} + \cdots + x_{2n}} n \Big ) ^ n} \leq \Big ( \frac {x_1 + x_2 + \cdots + x_{2n}} {2n} \Big) ^ {2n} \\
\Leftrightarrow & \boxed{x_1 x_2 \cdots x_n x_{n+1} \cdots x_{2n}} \leq \Big ( \frac {x_1 + x_2 + \cdots + x_{2n}} {2n} \Big) ^ {2n}
\end{aligned}
$$
注意:框出来的地方是 $P(n)$
1.9c
- $P(n) \Rightarrow P(2n)$
- $P(n) \Rightarrow P(n - 1)$
根据数论的理论便能证明。考察正整数集。
1.10
术语 (之后有关汉诺塔问题将延续这一术语):
- 原柱:$A$
- 中间柱:$M$
- 目标柱:$B$
- 将 $1 \sim (n-1)$ 圆盘从 B 移动到 A (表示操作或次数): $1 \sim (n - 1) : B \rightarrow A$
考察 $Q$:由于大盘 ($n$) 必须要移动,所以我们势必要把 $1 \sim (n - 1)$ 移动到 $M$,把 $n$ 移动到 $B$,再将 $M$ 上的 $1 \sim (n - 1)$ 移动到 $B$。
注意:$Q_n, R_n$ 皆为 最少 移动次数,而要移动大盘 $n$,上述描述的过程便是最少的。因为移动 $n$ 的充要条件就是 $B$ 柱空,$A$ 柱只有 $n$ 号盘,即 $M$ 柱上有 $1 \sim (n - 1)$。也就是说:
$$
Q_n = 1 + \min \{ 1\sim (n-1): A \rightarrow M\} + \min \{ 1\sim (n-1): M \rightarrow B\}
$$
由于都是逆时针,不难得出:
$$
\min \{ 1\sim (n-1): A \rightarrow M\} = \min \{ 1\sim (n-1): M \rightarrow B\} = R_{n-1}
$$
故
$$
Q_n = 1 + 2 R_{n-1}
$$
相似地,考察 $R$,由于大盘 $n$ 必须移动,且有顺序规定,我们得出了如下移动方案:
$$
1 \sim (n - 1) : B \rightarrow A
$$
$$
n : B \rightarrow M
$$
$$
1 \sim (n - 1) : A \rightarrow B
$$
$$
n : M \rightarrow A
$$
$$
1 \sim (n - 1) : B \rightarrow A
$$
最后次数为:
$$
R_n = \boxed{2 R_{n-1} + 1} + Q_{n-1} = Q_n + Q_{n-1}
$$
1.11
术语:下面的圆盘可能会有两种表达:
- $na$,大小为第 $n$ 大,原顺序中的第一个
- $nb$,大小为第 $n$ 大,原顺序中的第二个
- $2n$,指第 $2n$ 个,不区分先后
- $1 \sim 2n$,指第 1 到第 $2n$ 个,不区分先后
1.11a
设移动 $2n$ 个圆盘的次数为 $D_n$,考察 $2n$ 的情况:
$$
D_{n + 1} = 2 D_n + 2
$$
上述可以理解为:
$$
1 \sim (2n - 2) : A \rightarrow M
$$
$$
(2n-1), 2n : A \rightarrow B
$$
$$
1 \sim (2n - 2) : M \rightarrow B
$$
又
$$
D_1 = 2
$$
求得
$$
D_n = 2^{n + 1} - 2
$$
这里给出了一个上界构造。下界证明:大圆盘必须移动。Q.E.D.
1.11b
前置结论:1.11a 的结果就是除了最后两个 (2n-1), 2n 的圆盘顺序颠倒了,其余的 $2n-2$ 个都是正常顺序。
归纳法易证。初值状态略。假设 $n-1$ 的状态成立
则根据上一题我们给出的构造:
第一次操作:$1 \sim (2n - 2) : A \rightarrow M$
M 柱上的排列:
$$
1a, 1b, 2a, 2b \cdots, (n-2) a, (n-2)b, {\color{red}{(n-1)b, (n-1)a}}
$$
第二次操作:$(2n-1), 2n : A \rightarrow B$
B 柱上的排列:
$$
\color{red}{nb, na}
$$
第三次操作:$1 \sim (2n - 2) : M \rightarrow B$
$1 \sim (2n - 2)$ 的顺序变换过程:
$$
\begin{aligned}
& 1a, 1b, 2a, 2b \cdots, (n-2) a, (n-2)b, {\color{red}{(n-1)b, (n-1)a}} \\
\Rightarrow& 1a, 1b, 2a, 2b \cdots, (n-2) a, (n-2)b, {\color{red}{(n-1)a, (n-1)b}}
\end{aligned}
$$
B 柱上的排列:
$$
1a, 1b, 2a, 2b \cdots, (n-2) a, (n-2)b, (n-1)a, (n-1)b, {\color{red}{nb, na}}
$$
Q.E.D.
证明完前置结论,我们来看问题本身。下面是可以给出的最小构造:
$$
1 \sim 2(n-1): A \rightarrow B
$$
$$
na: A \rightarrow M
$$
$$
1 \sim 2(n-1): B \rightarrow M
$$
$$
nb: A \rightarrow B
$$
$$
1 \sim 2(n-1): M \rightarrow A
$$
$$
na: M \rightarrow B
$$
$$
1 \sim 2(n-1): A \rightarrow B
$$
由于 $1 \sim 2(n-1)$ 的变换经历了 4 次,也就是偶数次,所以颠倒的顺序又回来了,故无需担心,可以直接用上小问的 D_n。
将 $D_n$ 的符号改写为 $g(n)$,记我们所求的为 $f(n)$,可得:
$$
f(0) = 0
$$
$$
f(1) = 3
$$
$$
f(n) = 4g(n-1) + 3 = 2g(n) - 1, n > 1
$$
上述的一切构造了一个上界,但是我们仍然没有证明这个答案为什么是这个问题的下界。由于证明必定会非常冗长,这里给出证明思路。
同样地,考察大圆盘,只不过现在有两个大圆盘。论证我们构造的大圆盘的所有移动步骤是必须的,再论证为了让大圆盘那么移动,移动其他圆盘的步骤是最少的。
1.13
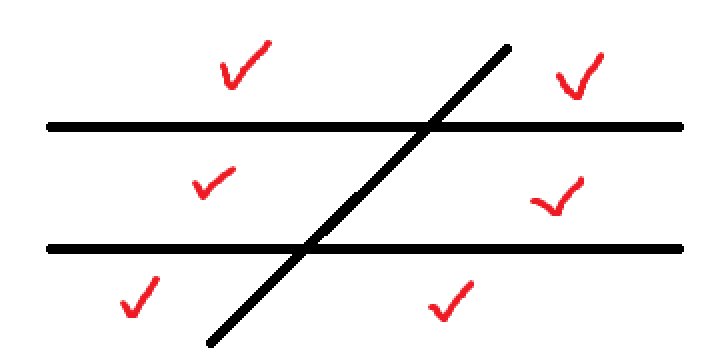
直接研究 Z 字形太过困难。这里我们研究化简的情况:两条平行线 + 一条斜线。即下面的这种情况:
记 $n$ 组上面这样的图形所划分出的区域的个数为 $P_n$。
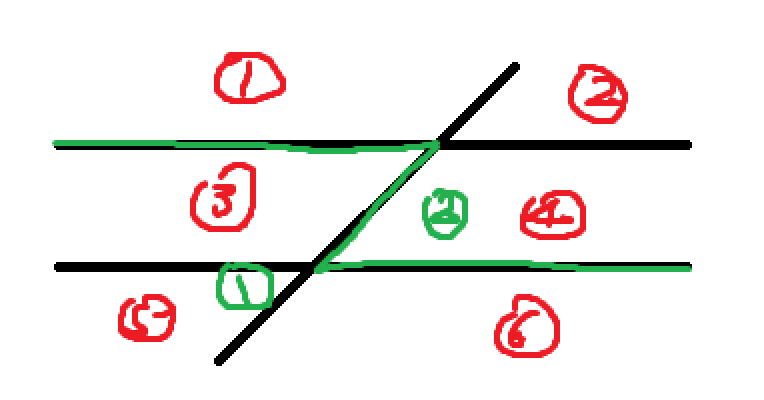
考察 $P_n$。分为两步:
- 至多存在 $2n$ 条互不平行的直线
- 至少存在 $n$ 条 与且仅与一条直线 平行的直线。
对于 Part (1),根据书的 1.2 节,对答案的贡献如下:
$$
L_{2n} = \frac {2n(2n + 1)} {2} + 1
$$
对于 Part (2),对答案的贡献其实只是原来的贡献减去每组平行线损失的 $1$,$n$ 组就是减去 $n$
所以我们得:
$$
P_{n} = L_{3n} - n
$$
接下来如法炮制,研究 Z 字形的损失:
对于每一组直线,损失为 4,故答案减去 $4n$
$$
Z_n = P_n - 4n = L_{3n} - 5n
$$
1.14
一个新空间是如何产生的?一个新空间必定由一个平面分割而成。所以对于第 $n$ 个平面,其能产生的最多的空间个数,就是这个平面和其他平面相交产生的相交线在其上能产生的最多的区域的个数。所以:
$$
f(n) = f(n - 1) + L(n - 1)
$$
1.15
这题看似困难,实则不然。我们一定要注意到一件事:除了初值条件不同,递推式和约瑟夫问题如出一辙!
$$
I(2n) = 2I(n) - 1
$$
$$
I(2n + 1) = 2I(n) + 1
$$
现在我们把目光转向初值:我们发现 $n=1$ 的时候,I(1) 没有意义,初值不存在!我们最少能找到的 $I$ 是
$$
I(2) = 2
$$
这个时候,我们想到了动态规划中常用的技巧:没有初值造初值,我们不妨进行反推用 $I(2)$ 来逆推 $I(1)$。但是!这个时候我们发现了问题:$I(1)$ 不仅可以由 $I(2)$ 逆推得来,也能由 $I(3)$ 逆推得来,而且值还不同!
$$
I(2) = 2 \Rightarrow I'(1) = \frac 3 2
$$
$$
I(3) = 1 \Rightarrow I''(1) = 0
$$
怎么办?很简单,分类讨论。我们首先搞清楚这两个不同的式子所对应的 $n$ 的情况。考察这两种情况的二进制位表示:
$$
I(2n) \rightarrow (10 \cdots)_2
$$
$$
I(2n + 1) \rightarrow (11 \cdots)_2
$$
所以我们就能给出两个范围:
$$
I(2n) \rightarrow n = 2^m + l, 0 \leq l < 2^{m-1}
$$
$$
I(2n + 1) \rightarrow n = 2^m + l, 2^{m-1} \leq l < 2^{m}
$$
接下来就简单了。还记得书上的成套方法结论吗?
$$
f(n) = 2^m \alpha + (2^m - 1 - l) \beta + l \gamma
$$
这里,我们有两个不同的 $\alpha$, 以及 $\beta = -1, \gamma = -1$。
答案略。
1.16
成套方法的简单应用。略。