注:本节内容为 CS:APP 第三版中文版 P73 的旁注。
内容
偏置技术:对于 $0 \leq k < w$,在执行算数位移时,C表达式 (x+(1<<k)-1)>>k 产生数值 $\lceil x / 2^k \rceil$
理解
我们不妨首先说明这个结论对于正数 (无论是无符号数还是补码数) 的正确性。
首先我们应该思考:在什么情况下我们会需要进行刻意的向上取整?答案是不能整除的时候。
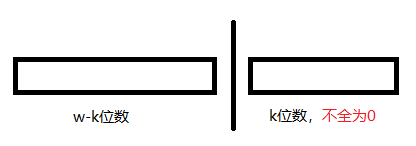
而在算术位移中何时不会被除尽?那只能是位移掉的部分有数的情况,即后 $k$ 位不全为 $0$,如下图:
接下来我们便可以分类讨论。我们希望:
- 被除尽时,什么都不做
- 在没被除尽时,让 $k+1$ 位加一
可以发现,(x+(1<<k)-1)>>k 完美地符合了我们的需要。+(1<<k) 先帮我们把一加上,然后如果能够除尽,刚好可以帮我们抵消掉加一的效果:
$$
[\cdots {\color{red} (+1)} ~~ 0 \cdots 0] - 1 = [\cdots (+0) ~~ {\color {red} 1 \cdots 1}]
$$
而对于除不尽的情况,因为后 $k$ 位有数,所以影响不到 $k+1$ 位,加一仍然能够生效。
至此,我们已经解释了为什么对于正数有效。
那么对于补码的负数呢?我们同样只需要考虑三点:
- 条件:注意到,从补码表示的定义出发,不被除尽的条件是相同的,依旧是后 $k$ 位不全为 $0$
- 最终目的:还是由补码的定义,除了最高位的位权是负的,其他位的位权都是正的。所以,「让 $k+1$ 位加一」同样是进行增加,所以是正确的。
- 可不可行:可行,因为无符号数加法和补码加法的位级表示相同,所以行为完全一致。
还有一个问题前面被回避了:操作时溢出?对于负数而言,只有在前 $w-k$ 位全为 $1$ 时,才有可能溢出。如果不进行向上取整,最后的结果是 -1,而溢出后的向上取整结果是 0,仍然符合我们的要求。