Zyzzyva

动机

PBFT 的 $O(n^2)$ 开销太大，而且观察到大多数时候并会经历 Primary Fault 甚至大多数时候不会有 Fault。Zyzzyva 旨在提高没有 Fault 或者没有 Primary Fault 的情况下的协议效率。

Zyzzyva 流程

一些记号的说明

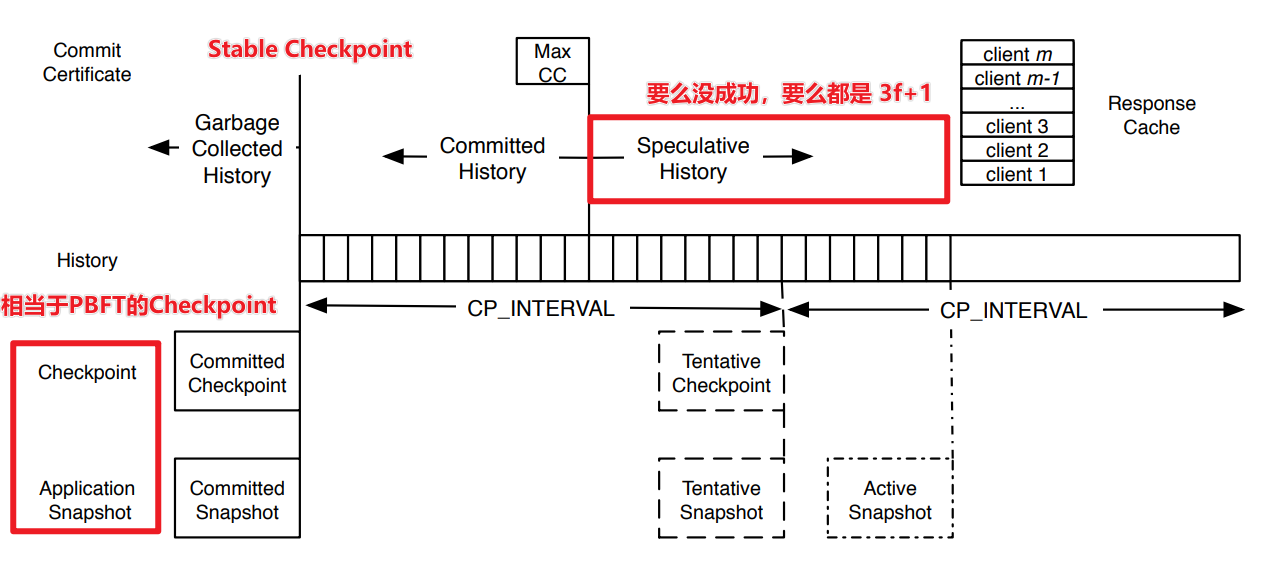
  • Checkpoint, CC, Speculative History 见上图
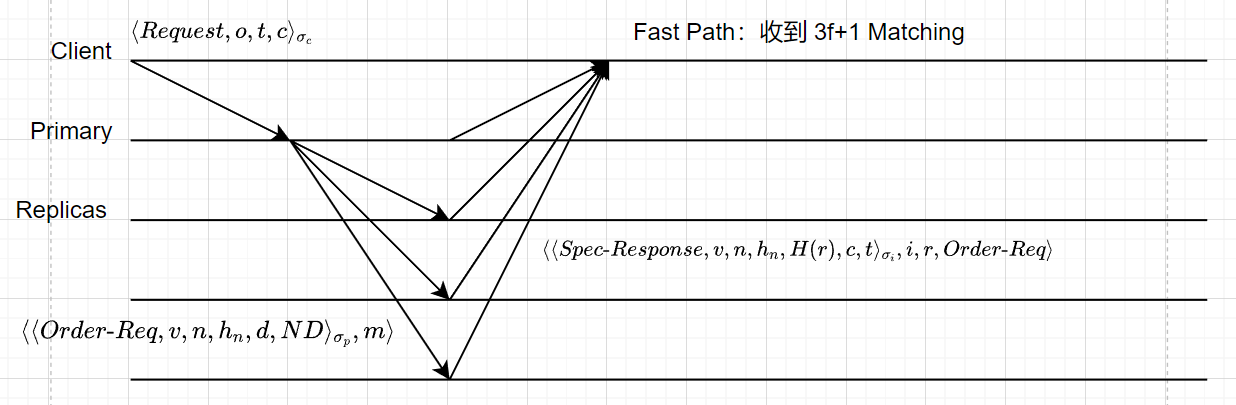
  • Order-Req 以及 Spec-Response阶段
    • $d = H(m)$，即消息 $m$ 的 Digest
    • $h_n = H(h_{n-1}, d)$，描述截止到 $n$ 的历史记录，即
      $$
      h_n = H(H(H(\cdots (H(d_1), d_2)\cdots), d_{n-2}), d_{n-1})
      $$
    • 注意到光靠 $h_n$ 就能判断历史记录了。正常的 Client 可以靠这个鉴别是否 Diverge。

Normal Case Operation

当有 Fault 存在

View Change

View Change 的大体过程和 PBFT 相同：

  • PBFT: Last Stable Checkpoint + Preprepare Messages
  • Zyzzyva: Last Stable Checkpoint / Committed Certificate + Speculative History

区别在于对待 Speculative History 的处理上。

Zyzzyva 这里要分两种情况处理：

  • 如果没有 Speculative History，那么就是普通的 PBFT View Change，没什么好讨论的
  • 如果有 Speculative History，我们需要判断这个 History Diverge 了还是是属于 Fast Path 的正常 History。判断方法如下：如果在 View Change 的 $2f+1$ 个 Replica 当中，有 $\geq f+1$ 个 Replica 有 CC 之后的这样一条匹配消息，那么就认为这个消息是真实消息，即属于 Fast Path。我们会在之后的章节给予证明。

一些 Intuition

对于 Zyzzyva，简要而言可以理解如下

  • 如果没有 Fault，那就非常快，Client 知道搞定就行了。这样的记录就是 Speculative 的
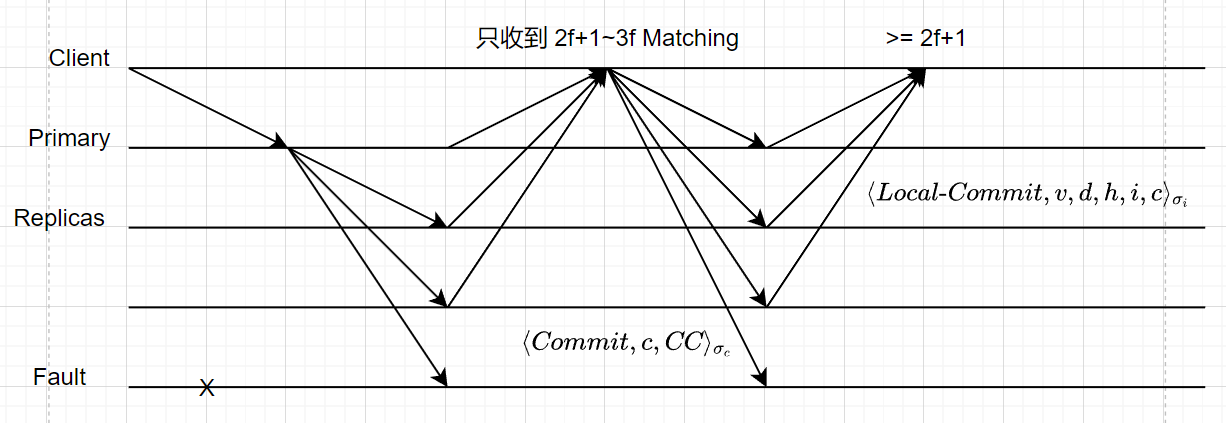
  • 如果存在 Fault，那也要至少要求 $2f+1$ 个 Reply，这个时候 Client 会给所有 Replica Multicast Committed Certificate。注意：有了 Committed Certificate，之前的所有 Speculative 记录就自动转正了
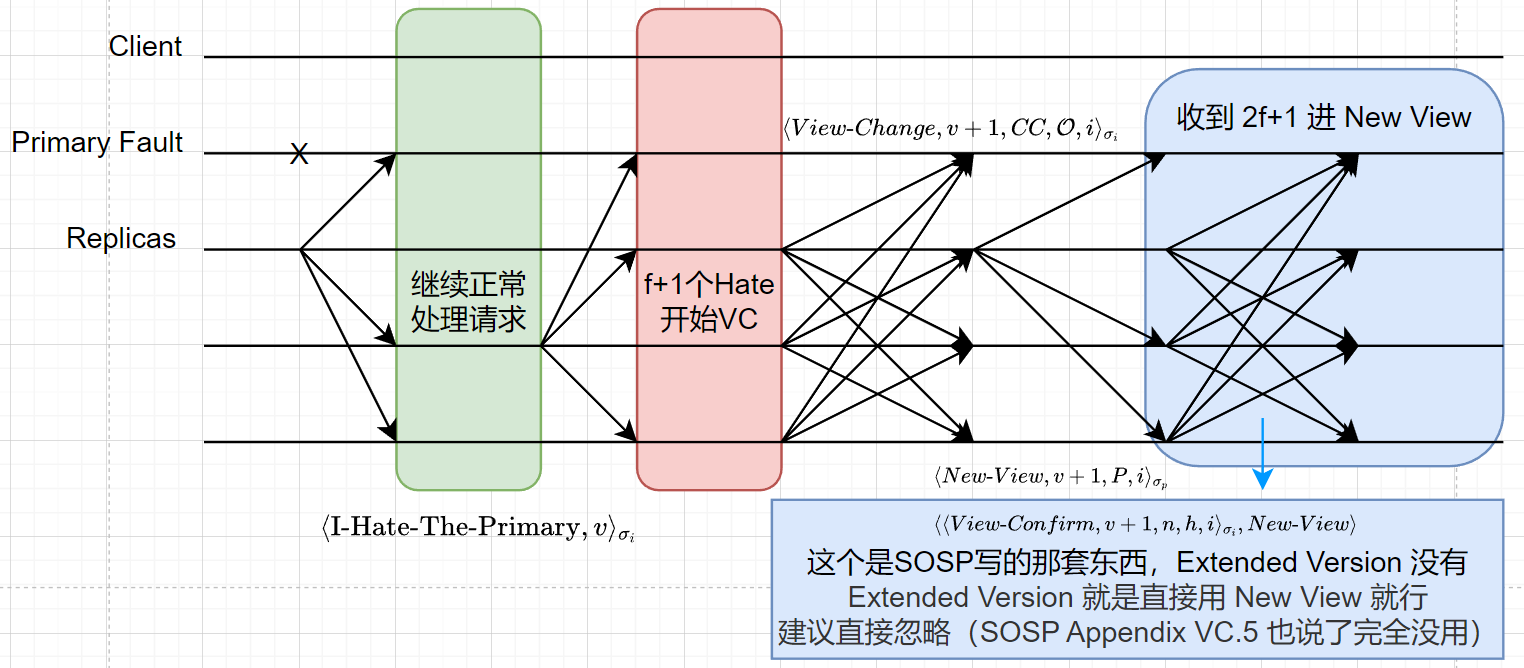
  • Zyzzyva 的 View Change 和 PBFT 相比也有少许不同。最大的特点就是：如果 Suspect Primary Faulty，不会暂停消息的处理！ Replica 会继续处理消息，但是同时广播 I-Hate-The-Primary。只有当 I-Hate-The-Primary 的数量达到 $f+1$ 的时候，才会进入真正的 View Change。相比之下，PBFT 只要 trigger timeout 就立刻罢工，这就是 PBFT 的 In-Dark 问题。

Safety 是如何保证的？

View 内部的 Safety？

注意到 Zyzzyva 没有 Pre-Prepare - Prepare - Commit 三个节点，没有 View 内的 Consensus，完全靠的是 CC 和 Speculative History。所以我们只需要分析这两个部分。

Committed Certificate 的 Safety

Committed Certificate 的 $2f+1$ 个 Replica 和 View Change 时的 $2f+1$ 个 Replica 构成了 $f+1$ 个 Quorum，保证了 View Change 的时候至少有一个 non-faulty Replica。这个和 PBFT 的过程相同，原理也相同。

Speculative History 的 Safety 以及 View Change 时的 $f+1$ 的 Design Choice

我们要论证的大问题是，有没有可能在前一个 View Commit 了一个消息，客户端接受了，但是在新的 View 中不见了？

首先我们可以证明：如果一个 Commit 属于 Fast Path ($3f+1$)，那么在 View Change 时，我们一定能在那个 $2f+1$ 的 Quorum 内找到 $f+1$ 个 Matching。

证明：反证法。如果一个 Commit 属于 Fast Path，同时找不到 $f+1$ 个 Matching，那么和至多有 $f$ 个节点是 Fault 矛盾。

接下来我们想要说明：如果一个 Commit 能够在 $2f+1$ 的 Quorum 中找到 $f+1$ Matching，那么他不可能属于 Slow Path（客户端成功执行）.

证明：反证法。如果一个 Commit 属于 Slow Path 且客户端成功执行，那么他必定存在于某个 CC 当中，与 Speculative History 矛盾。

给出了上面两种情形，我们接下来说明：如果一个 Commit 能够在 $2f+1$ 的 Quorum 中找到 $f+1$ Matching，那么把他包含进 New View 中时不会 Violate Safety Condition。

证明：根据前面几个结论，我们可以得到这个 Commit 无非只有两种情形：

  1. Commit 属于 Fast Track，成功执行：不会违反 Safety Condition
  2. Commit 属于 Slow Track，Commit Certificate 只有部分（或者没有）传回，而且根据前面的论证，$2f+1$ 的 View Change 节点内不可能有 CC。在这种情况下 View Change 会促成 Commit，即在 New View 继续处理这个消息。如果客户端请求失败了进行重传，那么 Cache 会继续这个过程。
  3. Commit 尚未执行完毕，即 Client 收到 $< 2f+1$ 个 Speculative Response：回顾本章开头的大问题，全然问题无。

如果 Diverge 了怎么办？

注意到 CC 前的内容不可能 Diverge，只有可能 Speculative History 有 Diverge。文章中没有讲解，但是如果有 Diverge 就听从 New View 安排，不对的东西直接 Rollback (Discard)，然后处理新的 Order-Request.

Two-Phase Protocol 的 View Change Liveness 问题

问题构造

与 PBFT 的对比

为什么 PBFT 没有这个问题？注意到 PBFT 的 View Change 原则是如果 Timeout 就自动发起 View Change，不会卡住。

解决方案——I Hate The Primary

解决方案就是 Intuition 章节提到的 I-Hate-The-Primary 消息。这里的主要思想是：只有我知道了足够多的人都怀疑 Primary Fault 的情况下，我才会进入 View Change，以防卡住的问题。这里我们可以证明为什么有 $f+1$ 个 I-Hate-The-Primary 就不会再有 liveness 问题。

注意到保证 liveness 的条件是没有 Network Partition。这就意味着 $f+1$ 个 I-Hate-The-Primary 一定可以被这 $f+1$ 个节点互相收到，也就是说会有 $f+1$ 个节点进入 View Change 节点并广播 View Change 消息。因为 Zyzzyva 和 PBFT 相同，在收到 $f+1$ 个其他节点的 View Change 之后，Replica 会立刻进入 View Change。而因为这里没有 Network Partition，所以上述操作必然可以完成，也就是说必然会有 $\geq 2f+1$ 的节点进入 View Change，完成整个操作。

有没有可能进行 View Change Attack？

参考最后一章 Design Choice 的 $f+1$ 设计问题。

Design Choice 问题汇总与 Edge Case 分析

  • Q: 为什么 Client 需要至少 $2f+1$ Matching？
  • Q: 为什么 View Change 至少需要 $2f+1$ Matching？
  • A: 这两个问题 Commited Certificate 的 Safety 章节已证明。
  • Q: 为什么 View Change 时 New Primary 计算，需要 $f+1$ 个 Ordered Request 存在才能将该记录加入 New View，而不像 PBFT 只需要 $1$ 个？
  • A: Speculative History 的 Safety 章节已证明。
  • Q: 为什么 I-Hate-The-Primary 需要 $f+1$ 个？
  • A: 我们在前面的章节已经证明了 $f+1$ 是足够的。这里我们再论证为什么 $f$ 是不行的。原因非常简单，如果需要 $f$ 个就可以进入 View Change 状态的话，假设有 $f$ 个 faulty Replica，全部不停地发 I-Hate-The-Primary，就会不断 trigger view change，liveness 便不能再保证了。
最后修改：2023 年 02 月 18 日 11 : 30 PM
© 允许规范转载
真的不买杯奶茶嘛....qwq