Preface
本文为我初三下时学习网络流的笔记整理,大多源自算法导论。当时学习的是网络流代数法建模。(手动@金牌教练)
证明思路
- 明确 Ford-Fulkerson 算法的思路:在残存网络找增广路,直到不存在增广路径为止
- 证明如果残存不存在增广路径等价于现在的网络流已经是最大流
Q&A
Q: 增广路会不会越变越多?或者说,在找增广路的过程中会不会陷入死循环?
A: 首先我们要明确:最大流问题在正权有向无环图上必定有解。而增广路必然会增广 $f$,所以增广路的条数必然是有限的,所以必然不会陷入死循环。
网络流的定义
网络流:$G = (V,E)$为一个有向图,每条边 $(u,v) \in E$都有一个非负的容量值,即$c(u,v) \geq 0$。对于每条边$(u,v) \in E$,不存在反向边$(v,u)$。若$(u,v) \notin E$,规定$c(u,v) = 0$,图中不允许出现环,即为有向无环图。在网络流的所有节点$v \in V$当中,存在两个特殊节点:源点$s$,汇点$t$。对于所有$v \in V - \{s,t\}$,都存在路径$s \rightsquigarrow v \rightsquigarrow t$,即所有节点都是互相联通的,对于每个节点,至少存在一条进入与离开的路径,即:$|E| ≥ |V| - 1$。
网络流的性质
-
容量限制(capacity constraint):对于每一条边$(u,v) \in E$,存在:
$$
0 ≤ f(u,v) ≤ c(u,v)
$$ -
流量守恒(flow conservation):对于每一个节点$v \in V - \{s,t\}$,必定存在:
$$
\sum_{u \in V} f(u,v) = \sum_{u \in V} f(v,u)
$$
其中,$f(u,v)$表示的是从节点$u \rightarrow v$的流。
上式成立是因为对于每个节点来说,流入流量必定等于流出流量。
在此,对一个图上的流$f$定义其的$|f|$值:
$$
|f| = \sum_{v\in V} f(s,v) - \sum_{v\in V} f(v,s)
$$
尽管在一个最大流当中,并不会存在流入源点的边,因此对于其来说上式的后半部分$\sum_{v\in V} f(v,s)$的值为$0$,但是这在稍后讨论的残存网络中会有应用。
最大流解决的问题
现在有一张有向无环图,将其想象成一个水管,水流会从高向低流,图中的每一条边就是一根水管,水流是单向的,而水流的方向就是图中边的方向。水在水管中流动时,会有一个流量限制,也就是它的最大容积,在这里每条边同样有流量限制,若$C_i$表示第$i$根水管的流量上限,$x_i$表示第$i$根水管当前的水流流量,则可以表示为:
$$
x_i \leq C_i,~i \in [1,n]
$$
在这个问题当中:$S$点和$T$点表示起点和终点。
在这个概念定义完成之后,便可以讨论最大流问题,也就是在一群水管当中(连接起点和终点),从起点到终点,最多可以流多少水。
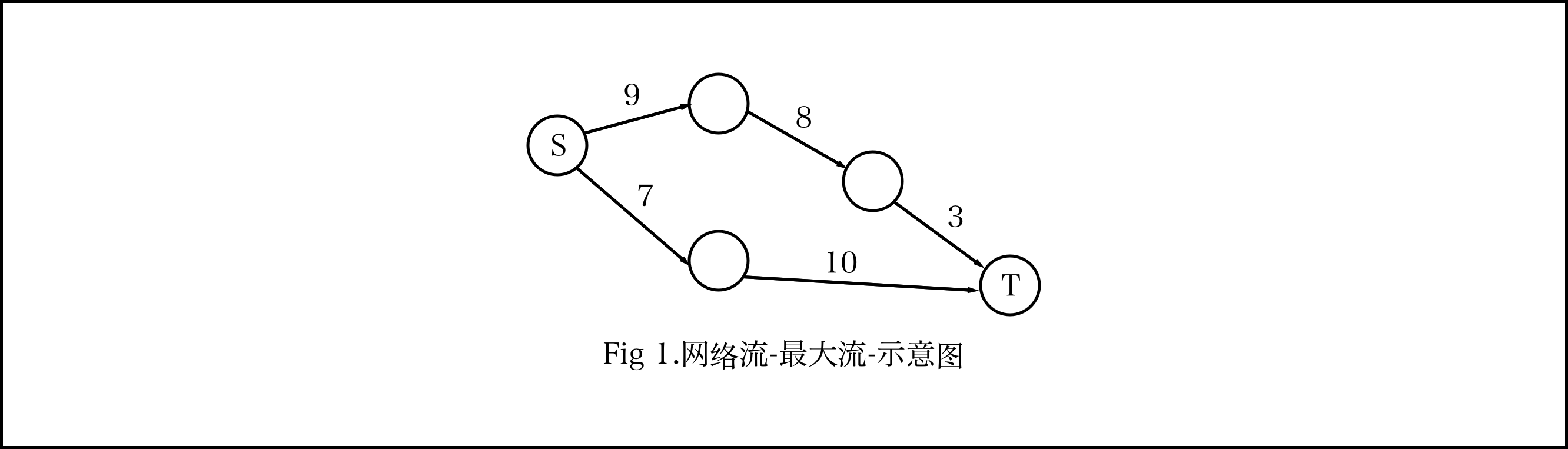
举一个简单形象的例子:先看下面这幅图,每条边代表的是最大流量:
很明显,这里有两条路可以走,首先看上面那条,显然能够流过的最大流量为3,另外一条则为7,所以由$S$到$T$的最大流为10:
上面是一个简单的例子,类似于这样的问题是最大流问题。
通过网络流的表述,可以将其表达为,需要求在满足网络流的两个性质的情况下:
$$
\max \{|f|\}
$$
其中$|f|$表示网络$G$的流,即为
$$
\begin {aligned}
&\max \{\sum_{v \in V} f(s,v) - \sum_{v \in V} f(v,s)\} \\
=&\max \{\sum_{v \in V} f(s,v) - 0\} \\
=&\max \{\sum_{v \in V} f(s,v)\}
\end {aligned}
$$
其根据流量守恒,亦为$\max\{\sum_{v\in V} f(v,t)\}$。
Ford-Fulkerson方法
对于一个网络$G$,存在对应的残存网络,每次在残存网络中寻找增广路径,当找到了一条增广路径,不难找出其原先对应的边,对于两个网络的这些边上的流进行修改,从而增加流的值,但是对于原图$G$来说,每一条增广路径却可能会对边增加或减少,但是这确实是非常必要的,比如在某一张有向图中,每个节点的值都相等,则若找到一条增广路径可能会使得其他增光路径消失,但是却会停止循环而得不到正确答案。虽然会不断增广,但是每次寻找的增广路径确实有源点出发,以汇点结束,所以总能使得$G$的流$f$不断增大。后面将进行证明。
$$
\begin {aligned}
&\text{FORD-FULKERSON-METHOD}(G,s,t) \\
&1~~~~\text{initialize flow } f \text{ to }0 \\
&2~~~~\mathbf{while} \text{ there exists an augmenting path } p \text{ in the residual network }G_f \\
&3~~~~~~~~\text{augument flow } f \text{ along }p\\
&4~~~~\mathbf{return}~f
\end {aligned}
$$
残存网络
残存网络记录的是流网络$G$中每条边的最大流量与当前流量之差。残存网络$G_f$由那些仍然可以调整流量的边构成。定义其残存容量$c_f(u,v) = c(u,v) - f(u,v)$,当$c_f$为正时,$(u,v)$仍可以添加流量,当$c_f(u,v) = 0$且$(u,v) \in E$时代表此边已满,所以$(u,v)$便不会是该残存网络的边。
同时由于前面的论述,需要给程序一个反悔的机会,所以一些不属于原网络的边也会出现在残余网络当中,那些边就是原网络的某些边的反向边,其的作用就是对这些边进行缩减。举个例子,若$(u,v) \in E$,为了表示一个正流量$f(u,v) > 0$的缩减,会将$(v,u)$添加入残余网络,由于原网络中不允许出现反向边,所以这样的行为不会产生任何问题。同样这样的操作又是必须的。
残余容量的定义:
$$
c_f(u,v) =
\begin {cases}
c(u,v) - f(u,v)~~&(u,v) \in E \\
f(v,u)&(v,u) \in E \\
0 &\text{otherwise}
\end {cases}
$$
所以在此给出残余网络的定义:给定一个流网络$G = (V,E)$和一个流$f$,由$f$所诱导的图$G$的残存网络为$G_f = (V, E_f)$,其中:
$$
E_f = \{(u,v)|c_f(u,v) > 0, (u,v) \in V\times V\}
$$
很容易证明:
$$
|E_f| ≤ 2|E|
$$
所以可以发现虽然残存网络不完全符合流网络的定义,但是其仍然遵循其性质,比如容量限制:
$$
0 ≤ f'(u,v) ≤ c_f(u,v), ~~(u,v) \in E_f
$$
顺带一提,对于残差网络,流量也是守恒的。
若$f$为网络$G$当中的一个流,$f'$为对应的残存网络$G_f$中的一个流,定义$f \uparrow f'$为流$f'$对$f$的递增,就是增加后状态的$f$,它是一个由$V \times V$到$\mathbb{R}$的一个函数:
$$
(f \uparrow f')(u,v) =
\begin {cases}
f(u,v) + f'(u,v) - f'(v,u) ~~~&(u,v) \in E\\
0 &\text{otherwise}
\end {cases}
$$
其中减少的是在残存网络中对应的$(u,v)$的反向边$(v,u)$的量,就是一种抵消的操作,和前文的操作一致。
定理$1$:设$G= (V,E)$为一个流网络,源点为$s$,汇点为$t$,设$f$为$G$中的一个流。设$G_f$为由流$f$所诱导的残存网络,设$f'$为$G_f$的一个流,那么定义的函数$f \uparrow f'$亦为$G$中的一个流,其值为$|f \uparrow f'| = |f| + |f'|$。其中$|\cdot|$符号所代表的就是网络的整个流。
证明:首先需要证明$f \uparrow f'$所构成的网络亦满足流网络的两个条件,即容量限制和流量守恒。
-
证明$f\uparrow f'$函数存在下界:若$(u,v) \in E$,则
$$
\begin {aligned}
~(f \uparrow f')(u,v) =&~f(u,v) + f'(u,v) - f'(v,u) \\
≥&~f(u,v) + f'(u,v) - f(u,v)~~~~~(\text{because }f'(v,u) ≤f(u,v)) \\
=&~f'(u,v) \\
≥&~0
\end {aligned}
$$ -
证明$f \uparrow f'$函数存在上界:若$(u,v) \in E$,则
$$
\begin {aligned}
(f \uparrow f')(u,v) =&~f(u,v) + f'(u,v) - f'(v,u) \\
≤&~f(u,v) + f'(u,v)~~~~~~~~~~~~~~~~~~~~(\text{because }f'(v,u) ≥ 0) \\
≤&~f(u,v) + c_f'(u,v) \\
=&~f(u,v) + c(u,v) - f(u,v) \\
=&~c(u,v)
\end {aligned}
$$
由前两点证明:函数$f\uparrow f'$存在上界下界,且上下界被容量约束,满足容量限制:
$$
0 ≤ (f\uparrow f')(u,v) ≤ c(u,v),~(u,v) \in E
$$
-
证明$f \uparrow f'$遵守流量守恒,由于$f,f’$均遵循流量守恒,即:
$$
\sum_{v\in V} f(u,v) = \sum_{v\in V} f(v,u),~ \sum_{v\in V} f'(u,v) = \sum_{v\in V} f'(v,u)
$$
所以
$$
\begin{aligned}
\sum_{v \in V} (f \uparrow f')(u,v) =&\sum_{v \in V} (f(u,v) + f'(u,v) - f'(v,u)) \\
=& \sum_{v \in V} f(u,v) + \sum_{v \in V}f'(u,v) - \sum_{v \in V}f'(v,u) \\
=& \sum_{v \in V} f(v,u) + \sum_{v \in V}f'(v,u) - \sum_{v \in V}f'(u,v) \\
=& \sum_{v \in V} (f(v,u) + f'(v,u) - f'(u,v)) \\
=& \sum_{v \in V} (f \uparrow f')(v,u)
\end{aligned}
$$ -
证明原式:设$V_1 = \{v|(s,v) \in E\}$,$V_2 = \{v|(v,s) \in E\}$。可以很容易得到:$V_1\cup V_2 \subseteq V$,$V_1 \cap V_2 = \varnothing$。
根据定义可以发现:
$$
\begin{aligned}
|f| &= \sum_{v \in V}f(s,v) - \sum_{v \in V} f(v,s) \\
&= \sum_{v \in V_1} f(s,v) - \sum_{v \in V_2} f(v,s)
\end {aligned}
$$
对于$f’$,由于$G_f$当中会存在反向边,所以:
$$
\begin {aligned}
|f'| &= \sum_{v \in V} f'(s,v) - \sum_{v \in V}f'(v,s) \\
&= \sum_{v\in V_1} f'(s,v) + \sum_{v\in V_2} f'(s,v) - \sum_{v\in V_1} f'(v,s) - \sum_{v\in V_2} f'(v,s)
\end {aligned}
$$
对于$|f\uparrow f’|$,由于$(f \uparrow f’)(u,v)$在$(u,v) \in E$时才可能不为零,所以同样地:
$$
\begin{aligned}
|f \uparrow f'| &= \sum_{v \in V} (f \uparrow f')(s,v) - \sum_{v \in V} (f \uparrow f')(v,s) \\
&= \sum_{v \in V_1} (f \uparrow f')(s,v) - \sum_{v \in V_2} (f \uparrow f')(v,s) \\
&= \sum_{v \in V_1} (f(s,v) + f'(s,v) - f'(v,s)) - \sum_{v \in V_2} (f(v,s) + f'(v,s) - f'(s,v)) \\
\end {aligned}
$$
所以可得:$|f \uparrow f’| = |f| + |f’|$,证毕。
增广路径
对于给定网络$G = (V,E)$和流$f$,增广路径为残存网络$G_f$中一条从$s$到$t$的路径,对于任意一条可以找到的路径$p$,这条路径的容量限制显而易见,为:
$$
c_f(p) = \min\{c_f(u,v), (u,v) \in p\}
$$
此时定义一个函数,也就是残存网络$G_f$的一个流:
$$
f_p(u,v) =
\begin {cases}
c_f(p)~~~~~&\text{if }(u,v) \text{ is on the route }p \\
0&\text{otherwise}
\end {cases}
$$
此时根据$f \uparrow f'$以及$f_p$的定义,若必然可以得到:
推论$1$:
$$
|f \uparrow f_p| = |f| + |f_p| > |f|
$$
因为 $|f_p| = c_f(p) > 0$.
其意义即为每次增广路径增广原路径时,原网络$G$中的$f(s,t)$将不断递增。也就是说,每次被增光之后,其总是比前一次更优的。
网络流的切割
对于流网络$G = (V,E)$中的一个切割,将节点集合$V$化为$S$和$T = V - S$,且满足$s \in S,~t\in T$。若$f$为一个流,则横跨切割$(S,T)$的净流量给出如下定义:
$$
f(S,T) = \sum_{u \in S}\sum_{v\in T}f(u,v) - \sum_{u\in S}\sum_{v\in T}f(v,u)
$$
切割$(S,T)$的容量是:
$$
c(S,T) = \sum_{u \in S}\sum_{v \in T} c(u,v)
$$
而对于网络$G$来说,其最小的切割就是切割容量的最小值。
注:这里的容量是单向的,因为要使网络切断,只需要计算从$S$到$T$的边的容量和,因为由$T$到$S$的边若不经过$S$到$T$是无法构成一条从$s$到$t$的路径,所以这种做法是有意义的。
定理$2$:设$f$为流网络$G$当中的一个流,该流网络的源点为$s$,汇点为$t$,设$(S,T)$为$G$的任意切割,存在$f(S,T) = |f|$。
证明:对于任意节点$u \in V -\{s,t\}$,由于其流量守恒,改写式子,得到:
$$
\sum_{v\in V}f(u,v) - \sum_{v\in V} f(v,u) = 0
$$
易得:
$$
\sum_{u\in S-\{s\}}(\sum_{v\in V}f(u,v) - \sum_{v\in V} f(v,u)) = 0
$$
因为 $t \notin S$。
所以:
$$
\begin{aligned}
|f| &= \sum_{v \in V} f(s,v) - \sum_{v \in V} f(v,s) \\
&= \sum_{v \in V} f(s,v) - \sum_{v \in V} f(v,s) + \sum_{u\in S-\{s\}}(\sum_{v\in V}f(u,v) - \sum_{v\in V} f(v,u)) \\
&= \sum_{v \in V} f(s,v) - \sum_{v \in V} f(v,s) + \sum_{u\in S-\{s\}}\sum_{v\in V}f(u,v) - \sum_{u\in S-\{s\}}\sum_{v\in V} f(v,u) \\
&= \sum_{v \in V}(f(s,v) + \sum_{u\in S - \{s\}}f(u,v)) - \sum_{v \in V}(f(v,s) + \sum_{u\in S -\{s\}}f(v,u)) \\
&=\sum_{v \in V}\sum_{u\in S} f(u,v) - \sum_{v \in V}\sum_{u\in S} f(v,u)
\end{aligned}
$$
由于$V = S \cup T$,$S \cap T = \varnothing$,所以可以将$V$按照$S$和$T$分解:
$$
\begin {aligned}
|f| &= \sum_{v \in V}\sum_{u \in S} f(u,v) - \sum_{v \in V}\sum_{u \in S} f(v,u) \\
&= \sum_{v \in S}\sum_{u \in S} f(u,v) + \sum_{v \in T}\sum_{u \in S} f(u,v) - \sum_{v \in S}\sum_{u \in S} f(v,u) - \sum_{v \in T}\sum_{u \in S} f(v,u) \\
&= (\sum_{u\in S}\sum_{v \in T}f(u,v) - \sum_{u\in S}\sum_{v \in T}f(v,u)) + (\sum_{v \in S}\sum_{u\in S}f(u,v) - \sum_{v \in S}\sum_{u\in S}f(v,u)) \\
&= (\sum_{u\in S}\sum_{v \in T}f(u,v) - \sum_{u\in S}\sum_{v \in T}f(v,u)) + 0 \\
&= f(S,T)
\end {aligned}
$$
证毕。
推论$2$:网络流$G$当中任意流$f$的值不能超过$G$的任意切割$(S,T)$的容量,即$|f| ≤ c(S,T)$。
证明:根据定理$2$易得:
$$
\begin {aligned}
|f| &= f(S,T) \\
&= \sum_{u \in S}\sum_{v\in T} f(u,v) - \sum_{u \in S}\sum_{v\in T} f(v,u) \\
&≤\sum_{u \in S}\sum_{v \in T}f(u,v) \\
&≤\sum_{u \in S}\sum_{v \in T}c(u,v) \\
&= c(S,T)
\end {aligned}
$$
证毕,但是这个推论非常具有意义,其意义为流的值不能超过割的容量,即最大流的值不能超过最小割的容量,即:
$$
\begin {aligned}
|f| ≤ |f|_{\max} ≤ c_{\min}(S,T) ≤ c(S,T)
\end {aligned}
$$
最大流最小割定理
设$f$为流网络$G = (V,E)$中的一个流,该流的源节点为$s$,汇点为$t$,则下面的条件是等价的:
- $f$为$G$的最大流。
- 残存网络$G_f$中不包含任何增广路径。
- $|f| = c(S,T)$,其中$(S,T)$为流网络$G$的某个切割。
证明:
$(1) \Rightarrow (2)$:使用反证法。假设$f$为网络$G$中的最大流,而其残存网络$G_f$中却又存在增广路径,根据推论$1$,设这条增广路径为$p$,则这条增广路径的流即为$f_p$且$f_p > 0$,那么由于推论$1$,必定存在$|f \uparrow f_p| = |f| + |f_p| > |f|$,此时$|f \uparrow f_p|$亦为$G$当中的流,但是其却是严格大于$|f|$的,所以与假设矛盾,故可得出若为最大流则不再存在增广路径的结论。
$(2) \Rightarrow (3)$:若残存网络$G_f$中不包括任何增广路径,也就是说,在残存网络$G_f$中不存在任何从源点$s$到汇点$t$的路径。定义$S = \{v | v \in V, (s,v) \in E_f\}$,$T = V - S$,显然,$s \in S, t \in T$,所以可以定义$(S,T)$为网络流$G$的一个切割。现在考虑一对节点$u \in S, v \in T$。讨论:
- $(u,v) \in E$,必定存在$f(u,v) = c(u,v)$,使得$c_f(u,v) = c(u,v) - f(u,v) = 0$。由于$G$中不存在反向边,所以$f(v,u) = 0$。
- $(v,u) \in E$,则必定有$f(v,u) = 0$,使得$c_f(u,v) = f(v,u) = 0$。
- $(u,v) \notin E, (v,u) \notin E$,则必定存在$f(u,v) = f(v,u) = c(u,v) = c(v,u) = 0 = c_f(u,v) = c_f(v,u)$。
根据上述三点可以得出无论何种情况,$f(v,u)$都为$0$,所以便可以根据定理$2$:$|f| = f(S,T)$列出方程并化简:
$$
\begin {aligned}
|f| &= f(S,T) = \sum_{u \in S}\sum_{v \in T}f(u,v) - \sum_{u \in S}\sum_{v \in T} f(v,u) \\
&= \sum_{u \in S}\sum_{v \in T}f(u,v) - \sum_{u \in S}\sum_{v \in T} 0 \\
&= c(S,T)
\end {aligned}
$$
所以得到$|f| = c(S,T)$。
$(3) \Rightarrow (1)$:根据推论$2$,对于所有切割$(S,T)$,$|f| ≤ c(S,T)$,由于现在$|f| = c(S,T)$,则证明此时$f$为最大流。
综上所述,此定理成立。
同样地,在此根据最大流最小割定理及推论$2$,可以简单得出结论:由于
$$
|f| = \max\{\sum_{v\in V} f(s,v) - \sum_{v\in V} f(v,s)\} \Leftrightarrow |f|_{\max} =c(S,T)
$$
所以根据推论$2$得出的不等式,若$f$为最大流,则:
$$
\begin {aligned}
&|f| ≤|f|_{\max} \\
\Rightarrow &|f| ≤|f|_{\max} = c_k(S,T),~ |f|_{\max} ≤ c(S,T) \\
\Rightarrow &c_k(S,T) ≤ c(S,T) \\
\Rightarrow &c_k(S,T) = \min\{c(S,T)\} \\
\Rightarrow &c_{\min}(S,T) = |f|_{\max}
\end {aligned}
$$
即证明了:
Ford-Fulkerson 算法
根据上一节的推导,不断地在残存网络中寻找增广路径$p$,使得$f$更新为$f \uparrow f_p$并且更新残存网络$G_f$的不断地迭代的过程中,知道不再存在增广路径时,根据最大流最小割定理,这个流$f$已经是最大流了:
$$
\begin {aligned}
&\text{FORD-FULKERSON}(G,s,t) \\
&1~~~~\mathbf{for}\text{ each edge }(u,v)\in G.E \\
&2~~~~~~~~~~~~(u,v).f = 0\\
&3~~~~\mathbf{while}\text{ there exist a path from }s\text{ to }t\text{ in the residual network }G_f \\
&4~~~~~~~~~~~~c_f(p) = \min\{c_f(u,v) ~| ~(u,v) \text{ is in the route }p\} \\
&5~~~~~~~~~~~~\mathbf{for }\text{ each edge }(u,v)\text{ in }p \\
&6~~~~~~~~~~~~~~~~~~~~\mathbf{if}\text{ }(u,v) \in E \\
&7~~~~~~~~~~~~~~~~~~~~~~~~~~~~(u,v).f = (u,v).f+c_f(p) \\
&8~~~~~~~~~~~~~~~~~~~~~~~~~~~~c_f(u,v) = c_f(u,v) - c_f(p) \\
&9~~~~~~~~~~~~~~~~~~~~~~~~~~~~c_f(v,u) = c_f(v,u) + c_f(p) \\
1&0~~~~~~~~~~~~~~~~~~~~\mathbf{else}\\
1&1~~~~~~~~~~~~~~~~~~~~~~~~~~~~(v,u).f = (v,u).f - c_f(p) \\
1&2~~~~~~~~~~~~~~~~~~~~~~~~~~~~c_f(v,u) = c_f(v,u) - c_f(p) \\
1&3~~~~~~~~~~~~~~~~~~~~~~~~~~~~c_f(u,v) = c_f(u,v) + c_f(p) \\
1&4~~~~\mathbf{return}\text{ }\sum_{v \in G.V}f(s,v)
\end {aligned}
$$
这是基本Ford-Fulkerson的算法,但是它很废,时间复杂度较高,而且当遇到某些奇葩网络的时候就会被强奸。之后我们会讨论他的优化:Dinic 算法。