欧几里得算法与扩展欧几里得算法
注:本节可以独立阅读,但同时也是 《具体数学》(原书第二版) 4.1 整除性 的旁注。
一个基本事实
记 $n = am + b$,其中 $n,m,a,b \in \mathbb Z$,则 $d$ 为 $m,n$ 的公因数当且仅当 $d$ 为 $m,b$ 的公因数。
证明:
充分性:
若 $d \mid m$,$d \mid n$ 则必有
$$
d \mid n-am \Leftrightarrow d \mid b
$$
又因为 $d \mid m$,所以 $d$ 为 $m,b$ 的公因数
必要性:
若 $d \mid m$,$d \mid b$ 则必有
$$
d \mid am + b \Leftrightarrow d \mid n
$$
故 $d \mid n, d\mid m$,即 $d$ 为 $m,n$ 的公因数。
Q.E.D.
由这个结论,我们能得出一个更强的结论:
$d$ 为 $m,n$ 的最大公因数当且仅当 $d$ 为 $m,b$ 的最大公因数。
证明:
由之前的结论:$m,n$ 的所有公因数所构成的集合必定等于 $m,b$ 所有公因数所构成的集合,即
$$
\{d \mid (d\mid m), (d\mid n)\} = \{d \mid (d\mid m), (d\mid b)\}
$$
对于每一个 $b = n-am, a\in \mathbb Z$ 都成立。
故
$$
\sup \{d \mid (d\mid m), (d\mid n)\} = \sup \{d \mid (d\mid m), (d\mid b)\}
$$
Q.E.D.
欧几里得算法
对于 $m, n \geq 0, m, n$ 不同时为零的两个数:
$$
\gcd(0,n) = n
$$
$$
\gcd(n,0) = n
$$
$$
\gcd(m,n) = \gcd(n \mod m, m), m > 0
$$
证明:
注意到
$$
n \mod m = n - m\lfloor n/m \rfloor
$$
即
$$
n = m\lfloor n/m \rfloor + (n\mod m)
$$
根据之前的引理:
$$
\gcd (n, m) = \gcd(m, n \mod m)
$$
即
$$
\gcd (m,n) = \gcd(n\mod m, m)
$$
由于在迭代过程中,值总是在变小,所以过程必定能结束。
欧几里得算法的程序实现
#include <iostream>
using namespace std;
int gcd(int m, int n) {
if (!m) return n;
return gcd(n % m, m);
}
int main() {
int m, n;
cin >> m >> n;
cout << "gcd: " << gcd(m, n) << endl;
return 0;
}关于负数的讨论:迭代过程中,绝对值一直在变小,所以过程必定能结束。虽然 C/C++ 中的取模和数学中的取模不一定完全一样,但是取模仍然意味着:
$$
a \text { mod' } b = a - kb, k \in \mathbb Z
$$
所以整个过程仍然是正确的,只不过最后可能相差一个符号,由于 $\gcd$ 恒正,我们顶多需要增加一个取绝对值的过程。
扩展欧几里得算法
扩展欧几里得主要研究下面这个式子:
$$
xm + yn = \gcd (m, n)
$$
试找出其的整数解 $(x, y)$。
我们可以发现,这个问题就是欧几里得算法的衍生产物。
温习欧几里得的迭代过程。我们分两部考虑这个问题
(1) 迭代终止:
当 $m = 0$ 时
$$
0*x + ny = n
$$
我们可以取
$$
x = 0, y = 1
$$
(2) 迭代还没有达到终止条件时:
$$
xm + yn = \gcd(m,n)
$$
取 $r = n \mod m$,作为欧几里得算法迭代时的额外产物,我们便可以得到一个类似的子问题:
$$
x'r + y'm = \gcd(r,m)
$$
注意到,我们已经证明了
$$
\gcd(m, n) = \gcd(r, m)
$$
即
$$
\begin{aligned}
&x'r + y'm = \gcd(m,n) \\
\Leftrightarrow~&x'(n - m\lfloor n/m\rfloor) + y'm = \gcd(m, n) \\
\Leftrightarrow~&(y'-\lfloor n/m\rfloor x')m + x'n = \gcd(m,n)
\end{aligned}
$$
所以,只要解决了我们的子问题,解出了 $x', y'$,我们就能算出 $x, y$:
$$
x = y'- \lfloor n/m \rfloor x'
$$
$$
y = x'
$$
由此,我们结束了迭代过程的描述。
扩展欧几里得的程序实现
#include <iostream>
using namespace std;
int exgcd(int m, int n, int &x, int &y) {
if (!m) {
x = 0; y = 1;
return n;
}
int d = exgcd(n % m, m, x, y);
int y1 = x;
x = y - n / m * x;
y = y1;
return d;
}
int main() {
int m, n;
cin >> m >> n;
int x, y;
int d = exgcd(m, n, x, y);
cout << "gcd: " << d << endl;
cout << x << " * " << m << " + " << y << " * " << n << " = " << d << endl;
return 0;
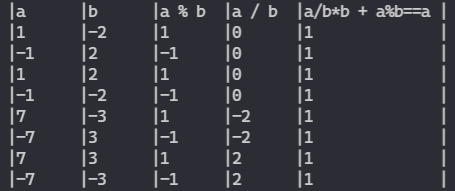
}注意:虽然 C/C++ 中,整数除法不一定是向下取整,取模也不是数学定义的取模,但是不影响我们这样写的正确性。因为,我们在证明中用到的取模和向下取整,其实只需要下面的恒等式成立:
$$
m = n \lfloor m/n \rfloor + (m \mod n)
$$
而在 C/C++ 中:
$$
m = (m / n) * n + m \% n
$$
是一个等价结论,所以我们可以理所当然地使用 / 和 % 符号进行运算替换。
下面是一些打表验证:
再者,是关于负数的讨论。前面提到了,普通的欧几里得算法对于负数可能导致一个符号的相反,而在这里,如果符号相反了,我们只需要对 $x, y, \gcd$ 都乘上一个负一即可。
此外,扩欧还蕴含了如下事实:对于 $m, n \in \mathbb N$,且不同是为零,我们总能找到 $x,y\in \mathbb Z$,使得 $xm+yn=\gcd(m,n)$。