- Preface
- BST 的问题
- 解决方案之一——Splay
- 右旋 (Zig)、左旋 (Zag)
- 如何判断是要左旋还是右旋?
- Splay 操作【上旋 (旋转到根)】
- 代码层面的数据结构维护
- 一些辅助函数
- 旋转的代码实现
- Splay 的代码实现
- 插入操作
- 两种查询寻
- 删除操作、寻找前继、寻找后继
- 代码
- Reference
Preface
昨天写了最普通的 BST,今天来写一下 Splay。注意:这一节建立在已经能够理解普通的二叉搜索树的基础上,若有疑问,见上一篇博客。
BST 的问题
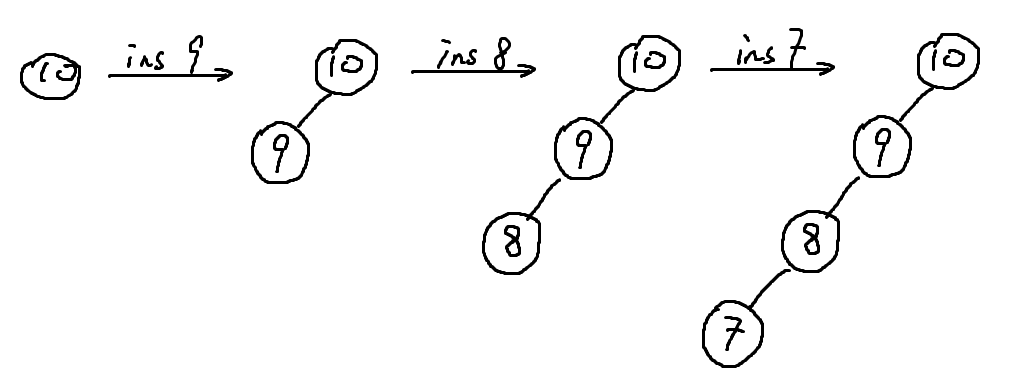
首先我们要意识到,最普通的 BST 可能会退化成链。通过插入大小递减的数,我们就可以轻易地让二叉树退化成链,从而是复杂度达到最坏复杂度 $O(n)$。
解决方案之一——Splay
Splay 可以解决这样的问题,最然最坏复杂度也是 $O(n)$,但是可以证明,连续的 $m$ 个操作的复杂可以降到 $O(m\log n)$,即均摊复杂度为 $O(\log n)$。这里不给出 Splay 复杂度的证明,可由势能分析证明。我们主要讲一下 Splay 的思想。
Splay 的核心在于,每次操作之后,我们都将该操作对应的节点旋转到根的位置。注意:这里使用了 旋转 一词。接下来我们来解释旋转的过程。
右旋 (Zig)、左旋 (Zag)
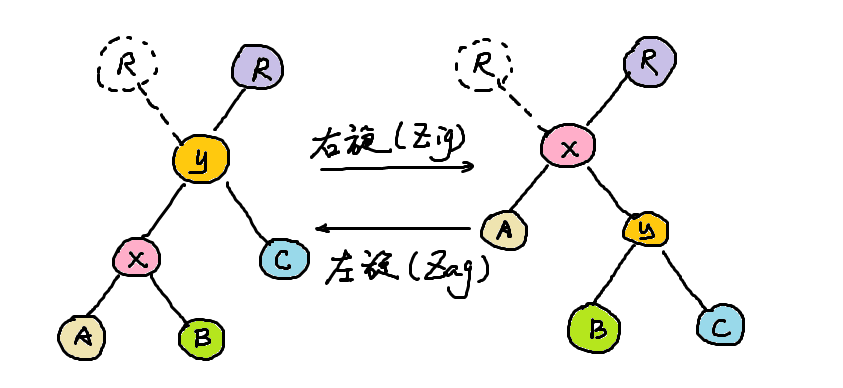
要解释「旋转到根」,我们先要引入两个概念:左旋与右旋。
为什么叫右旋和左旋?因为我们是把位置较低的元素 (x / y) 向 (右 / 左) 旋转,达到了较高的位置。
注意:在这张图中,我画了两个 R,意思是 x / y 无论是 R 的左儿子还是右儿子,这个旋转的结果都是不变的。
接下来我们来证明右旋和左旋不会改变二叉树的性质,能让其依旧满足二叉搜索树的定义。
证明:
由于二叉搜索树是递归定义的,所以我们只需要证明图中出现的有限个节点的大小关系保持不变即可。
左图的关系:
$$
A < x < B
$$
$$
x < y < C
$$
$$
B < y
$$
右图的关系:
$$
A < x < y
$$
$$
B < y < C
$$
$$
B > x
$$
不难发现,通过代数变换,就能证明这两个不等式组是完全等价的。
如何判断是要左旋还是右旋?
答案很简单,如果我们要往上旋转的儿子是左儿子,那就右旋,如果是右儿子,那就左旋。
Splay 操作【上旋 (旋转到根)】
我们之前已经介绍了左旋与右旋,其可以把一个节点 x 降低一个深度 (上移一个单位)。那如果我们想要把一个节点上移使之成为根节点,那我们就需要进行若干个左旋和右旋操作来达成这一问题。
接下来我们来介绍迭代过程中的三种大类型。
(1) 该节点的父亲就是根节点:旋一次,结束迭代
(2) 根节点不是父亲,并且父亲的儿子类型和该节点的儿子类型相同【比方说:父亲是祖父的左儿子,这个节点也是父亲的左儿子】
这种情况下,先旋一次父亲,再旋一次自身
(3) 根节点不是父亲,并且父亲的儿子类型和该节点的儿子类型不同【比方说:父亲是祖父的左儿子,这个节点也是父亲的右儿子】
这种情况下,直接自旋两次即可。
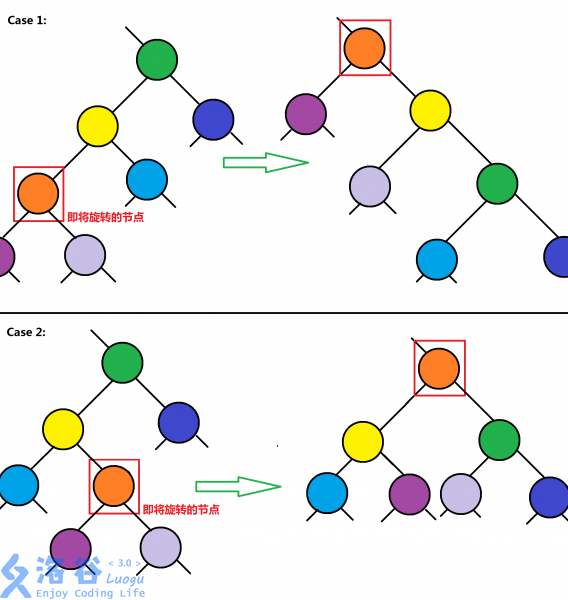
有一张图可以很好地解释 (2) 和 (3),分别对应图中的 Case 1 和 Case 2
代码层面的数据结构维护
为了方便维护,我们定义如下 struct 以及数据:
int cnt = 0; // 维护节点数
int rt = 0; // 根的节点编号
struct node {
int val, // 这个节点所代表的值
cnt, // 这个值出现的次数
sz, // 以这个节点为根的子树的大小
fa, // 父节点编号
ch[2]; // ch[0] 左儿子;ch[1] 右儿子
} t[maxn];一些辅助函数
// 调试用,遍历 Splay
void print(int u) {
if (!u) return;
print(t[u].ch[0]);
for (int i = 0; i < t[u].cnt; i ++) cout << t[u].val << ' ';
print(t[u].ch[1]);
}
// 更新 u 的 size(重新计算)
void update_sz(int u) {
t[u].sz = t[t[u].ch[0]].sz + t[u].cnt + t[t[u].ch[1]].sz;
}
// 查询 u 是其父亲的左儿子还是右儿子
int identify(int u) {
return t[t[u].fa].ch[1] == u;
}
// 清除编号为 u 的所有值(在删除节点的时候会用到)
void clear(int u) {
t[u] = (node) {0, 0, 0, 0, 0, 0};
}
// let u be fa's [ch] son
// 让 u 成为 fa 的 [ch] (0, 1 左右) 儿子
void connect(int u, int fa, int ch) {
t[u].fa = fa;
t[fa].ch[ch] = u;
}旋转的代码实现
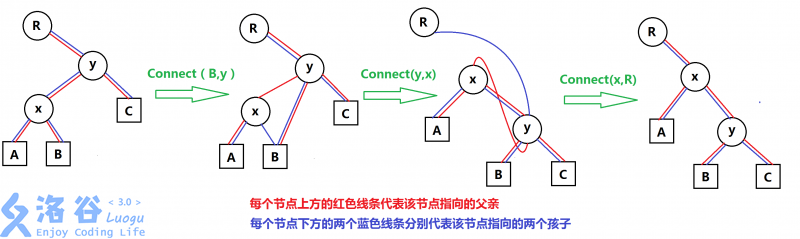
这里有一张非常不错的图:
可以用我们前面定义的 connect 函数来进行右旋。左旋也是类似的。
这里有一个技巧:B 对于 x 和 x 对于 y 的儿子类型总归是相反的。所以我们可以使用位运算技巧,一次性写完左旋和右旋。
void rotate(int x) {
int y = t[x].fa;
int R = t[y].fa;
int R_ch = identify(y), y_ch = identify(x);
// B 为 x 的儿子
// 若 x 为 y 的左儿子,则 B 为 x 的右儿子,执行右旋 zig
// 若 x 为 y 的右儿子,则 B 为 x 的左儿子,执行左旋 zag
int B = t[x].ch[y_ch ^ 1];
connect(B, y, y_ch);
connect(y, x, y_ch ^ 1);
connect(x, R, R_ch);
update_sz(y); update_sz(x);
}Splay 的代码实现
void splay(int u) {
// 解释一下下面这个循环:
// 1. 只要有父亲就至少会旋 1 次 (先 rotate(u) 再更新 fa 然后判断新 fa)
// 2. 如果父亲没有父亲就只旋 1 次
// 这个循环对应了 splay 的三种操作
// 1. 若父亲是根,也就是父亲没有父亲,只旋 1 次
// 2. 若父亲不是根,且当前节点的儿子类型和父亲的儿子类型相同,先旋父亲再旋自己
// 3. 若父亲不是根,且当前节点的儿子类型和父亲的儿子类型不同,旋两次自己
for (int fa = t[u].fa; fa = t[u].fa, fa; rotate(u))
if (t[fa].fa) rotate(identify(u) == identify(fa) ? fa : u);
rt = u;
}插入操作
我写的插入操作和普通的 BST 几乎没有区别,只不过有以下要点需要注意:
- 插入后要以插入完成的节点为目标进行 Splay
- 插入值可能已经存在,所以要 Splay 的目标并不一定是
cnt
int insert(int &u, int fa, int val) {
if (!u) {
t[u = ++ cnt] = (node) {val, 1, 1, fa, 0, 0};
return u;
}
t[u].sz ++;
if (t[u].val == val) {
t[u].cnt ++;
return u;
}
else return insert(t[u].ch[val > t[u].val], u, val);
}
void insert_splay(int val) {
if (!cnt) {
rt ++;
t[++ cnt] = (node) {val, 1, 1, 0, 0, 0};
return;
}
int u = insert(rt, 0, val);
splay(u);
}两种查询寻
两种查询操作和标准 BST 基本上一样,除了要添加 Splay 操作。
int query_rank(int u, int val) {
if (u == 0) {
splay(t[u].fa);
return 1;
}
if (t[u].val == val) {
int ans = t[t[u].ch[0]].sz + 1;
splay(u);
return ans;
}
if (val < t[u].val) return query_rank(t[u].ch[0], val);
return t[t[u].ch[0]].sz + t[u].cnt + query_rank(t[u].ch[1], val);
}
int query_val(int u, int rank) {
if (rank > t[t[u].ch[0]].sz && rank <= t[t[u].ch[0]].sz + t[u].cnt) return t[u].val;
if (rank <= t[t[u].ch[0]].sz) return query_val(t[u].ch[0], rank);
return query_val(t[u].ch[1], rank - t[t[u].ch[0]].sz - t[u].cnt);
}删除操作、寻找前继、寻找后继
删除非常有讲究。在写删除之前,我们不妨先考虑一下前继和后继怎么寻找。借助 Splay,我们发现,寻找前继就等于:
(1) 先插入一个我们要寻找的数
(2) 把我们要寻找的数 Splay 到根(插入的时候已经自动帮我们做了)
(3) 根的左子树的最大值便是前继(先往左跳,再不停地往右跳直到结束)
(4) 删除插入的值
而寻找后继就是:
(1) 先插入一个我们要寻找的数
(2) 把我们要寻找的数 Splay 到根(插入的时候已经自动帮我们做了)
(3) 根的右子树的最大值便是前继(先往右跳,再不停地往左跳直到结束)
(4) 删除插入的值
所以,我们可以给出除了 splay, 插入和删除这三个模块以外地寻找前后继的代码:
int pre() {
int cur = t[rt].ch[0];
if (!cur) return cur;
while (t[cur].ch[1]) cur = t[cur].ch[1];
splay(cur);
return cur;
}
int nxt() {
int cur = t[rt].ch[1];
if (!cur) return cur;
while (t[cur].ch[0]) cur = t[cur].ch[0];
splay(cur);
return cur;
}接下来,我们再来谈删除。我们不妨先把需要删除的节点 Splay 到根,然后分类讨论。
(1) 出现次数大于 1,直接 cnt --,结束。
(2) 需要删除这个节点。
第二种情况又有三种情况:
(1) 就剩他一个节点,那就全部删光
(2) 只剩一个儿子,左儿子或者右儿子,这种情况下很容易就能够构造,具体操作见代码
(3) 两个儿子都在。这种情况比较复杂,我们着重讨论。我们可以证明:如下的操作是正确的:
- 寻找左子树的最大值,即需删除节点的前继
- 将这个前继 Splay 到根
- 将原来的右儿子作为现在根的右儿子
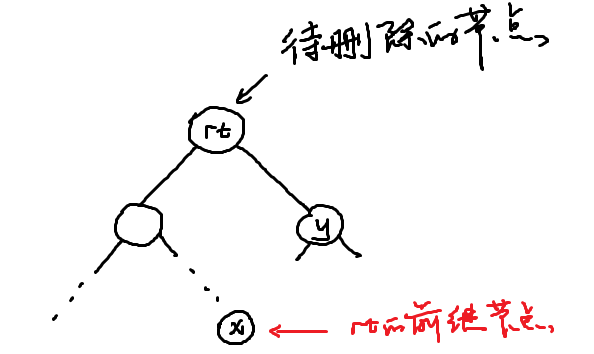
我们不妨画个图来证明这样做的正确性。下图是最初始的情况:
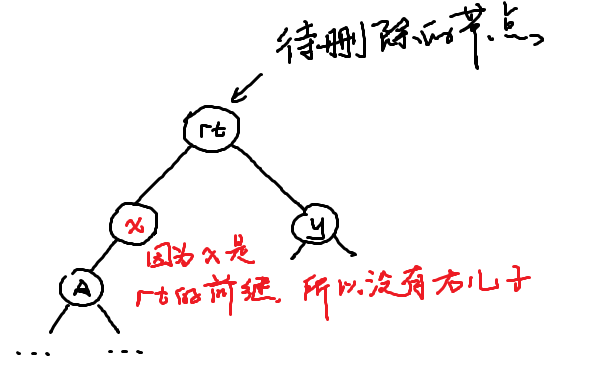
我们第一步要进行的操作是要将 x Splay 到根。那我们不妨考察其 Splay 到根之前的情况。由于 x 是前继的性质,所以 x 就是 rt 先向左然后一路向右,所以最后我们必然会达到这样的情况:
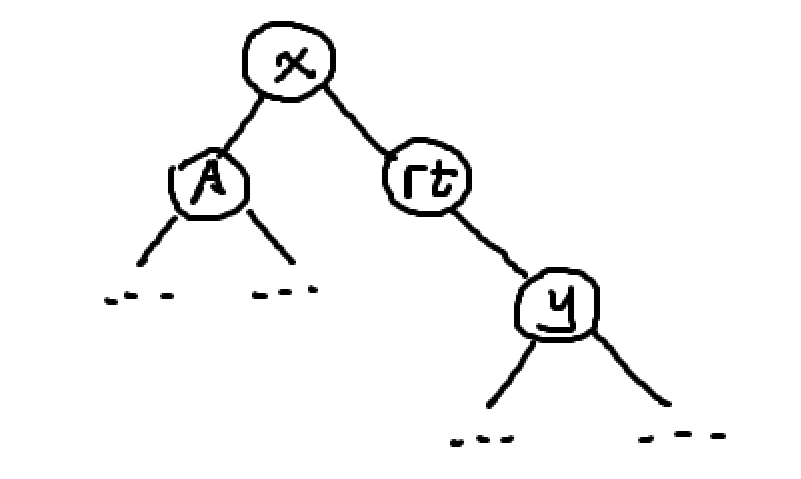
经过右旋,自然而然就能达到:
证明了结论的正确性。
代码:
void del(int k) {
query_rank(rt, k); // 将待删除的元素 Splay 到根
if (t[rt].cnt > 1) {
t[rt].cnt --; t[rt].sz --;
return;
}
// 全没了
if (!t[rt].ch[0] && !t[rt].ch[1]) {
clear(rt);
rt = cnt = 0;
return;
}
if (!t[rt].ch[0]) {
int old_rt = rt;
rt = t[rt].ch[1];
t[rt].fa = 0;
clear(old_rt);
return;
}
if (!t[rt].ch[1]) {
int old_rt = rt;
rt = t[rt].ch[0];
t[rt].fa = 0;
clear(old_rt);
return;
}
int old_rt = rt, y = t[rt].ch[1];
int x = pre();
t[x].ch[1] = y; t[y].fa = x;
clear(old_rt);
update_sz(rt);
}代码
测试传送门:https://www.luogu.com.cn/problem/P3369
#include <iostream>
#define fuck cout << __LINE__ << endl
using namespace std;
const int maxn = 1e5+5;
int cnt = 0, rt = 0;
struct node { int val, cnt, sz, fa, ch[2]; } t[maxn];
void print(int u) {
if (!u) return;
print(t[u].ch[0]);
for (int i = 0; i < t[u].cnt; i ++) cout << t[u].val << ' ';
print(t[u].ch[1]);
}
void update_sz(int u) {
t[u].sz = t[t[u].ch[0]].sz + t[u].cnt + t[t[u].ch[1]].sz;
}
int identify(int u) {
return t[t[u].fa].ch[1] == u;
}
void clear(int u) {
t[u] = (node) {0, 0, 0, 0, 0, 0};
}
// let u be fa's [ch] son
// 让 u 成为 fa 的 [ch] (0, 1 左右) 儿子
void connect(int u, int fa, int ch) {
t[u].fa = fa;
t[fa].ch[ch] = u;
}
void rotate(int x) {
int y = t[x].fa;
int R = t[y].fa;
int R_ch = identify(y), y_ch = identify(x);
// B 为 x 的儿子
// 若 x 为 y 的左儿子,则 B 为 x 的右儿子,执行右旋 zig
// 若 x 为 y 的右儿子,则 B 为 x 的左儿子,执行左旋 zag
int B = t[x].ch[y_ch ^ 1];
connect(B, y, y_ch);
connect(y, x, y_ch ^ 1);
connect(x, R, R_ch);
update_sz(y); update_sz(x);
}
void splay(int u) {
// 解释一下下面这个循环:
// 1. 只要有父亲就至少会旋 1 次 (先 rotate(u) 再更新 fa 然后判断新 fa)
// 2. 如果父亲没有父亲就只旋 1 次
// 这个循环对应了 splay 的三种操作
// 1. 若父亲是根,也就是父亲没有父亲,只旋 1 次
// 2. 若父亲不是根,且当前节点的儿子类型和父亲的儿子类型相同,先旋父亲再旋自己
// 3. 若父亲不是根,且当前节点的儿子类型和父亲的儿子类型不同,旋两次自己
for (int fa = t[u].fa; fa = t[u].fa, fa; rotate(u))
if (t[fa].fa) rotate(identify(u) == identify(fa) ? fa : u);
rt = u;
}
int insert(int &u, int fa, int val) {
if (!u) {
t[u = ++ cnt] = (node) {val, 1, 1, fa, 0, 0};
return u;
}
t[u].sz ++;
if (t[u].val == val) {
t[u].cnt ++;
return u;
}
else return insert(t[u].ch[val > t[u].val], u, val);
}
void insert_splay(int val) {
if (!cnt) {
rt ++;
t[++ cnt] = (node) {val, 1, 1, 0, 0, 0};
return;
}
int u = insert(rt, 0, val);
splay(u);
}
int pre() {
int cur = t[rt].ch[0];
if (!cur) return cur;
while (t[cur].ch[1]) cur = t[cur].ch[1];
splay(cur);
return cur;
}
int nxt() {
int cur = t[rt].ch[1];
if (!cur) return cur;
while (t[cur].ch[0]) cur = t[cur].ch[0];
splay(cur);
return cur;
}
int query_rank(int u, int val) {
if (u == 0) {
splay(t[u].fa);
return 1;
}
if (t[u].val == val) {
int ans = t[t[u].ch[0]].sz + 1;
splay(u);
return ans;
}
if (val < t[u].val) return query_rank(t[u].ch[0], val);
return t[t[u].ch[0]].sz + t[u].cnt + query_rank(t[u].ch[1], val);
}
int query_val(int u, int rank) {
if (rank > t[t[u].ch[0]].sz && rank <= t[t[u].ch[0]].sz + t[u].cnt) return t[u].val;
if (rank <= t[t[u].ch[0]].sz) return query_val(t[u].ch[0], rank);
return query_val(t[u].ch[1], rank - t[t[u].ch[0]].sz - t[u].cnt);
}
void del(int k) {
query_rank(rt, k);
if (t[rt].cnt > 1) {
t[rt].cnt --; t[rt].sz --;
return;
}
// 全没了
if (!t[rt].ch[0] && !t[rt].ch[1]) {
clear(rt);
rt = cnt = 0;
return;
}
if (!t[rt].ch[0]) {
int old_rt = rt;
rt = t[rt].ch[1];
t[rt].fa = 0;
clear(old_rt);
return;
}
if (!t[rt].ch[1]) {
int old_rt = rt;
rt = t[rt].ch[0];
t[rt].fa = 0;
clear(old_rt);
return;
}
int old_rt = rt, y = t[rt].ch[1];
int x = pre();
t[x].ch[1] = y; t[y].fa = x;
clear(old_rt);
update_sz(rt);
}
int main() {
int n, opt, x; cin >> n;
while (n --> 0) {
cin >> opt >> x;
if (opt == 1)
insert_splay(x);
else if (opt == 2)
del(x);
else if (opt == 3)
cout << query_rank(rt, x) << endl;
else if (opt == 4)
cout << query_val(rt, x) << endl;
else if (opt == 5) {
insert_splay(x);
cout << t[pre()].val << endl;
del(x);
} else {
insert_splay(x);
cout << t[nxt()].val << endl;
del(x);
}
}
return 0;
}