CEOI 2011 Traffic (P4700)

题面

题目：

测试传送门：

https://www.luogu.com.cn/problem/P4700

题解

首先分析复杂度，我们需要在 $O(n)$ 的时间内搞定。不难得出，暴力非常简单，只要从左侧每个点开始 BFS 即可。但是这样的复杂度显然是 $O(n^2)$，直接会 TLE。我们需要优化。

下面有一个小结论：

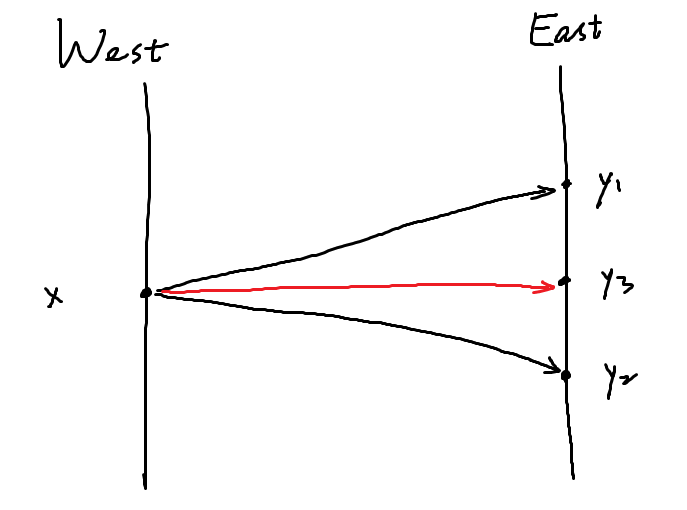
筛选出所有东海岸的可达点之后，所有对于西海岸的每一个点，东海岸的可达点都是连续的，不会间断。用图中的意思就是如果 $y_1, y_2, y_3$ 都存在西海岸的某一个 $x_i$ 使之可达，那么如果西海岸的某一个点 $x$ 能够达到 $y_1$ 和 $y_2$，那么也一定可达到 $y_3$。

证明：

反证法。如果 $y_3$ 对于 $x$ 不可达，那么 $y_3$ 势必可以到达西海岸的其他点，因为 $y_3$ 是一个可达点。那么西海岸的其他点只有两种情况：

在 $x$ 北
在 $x$ 南

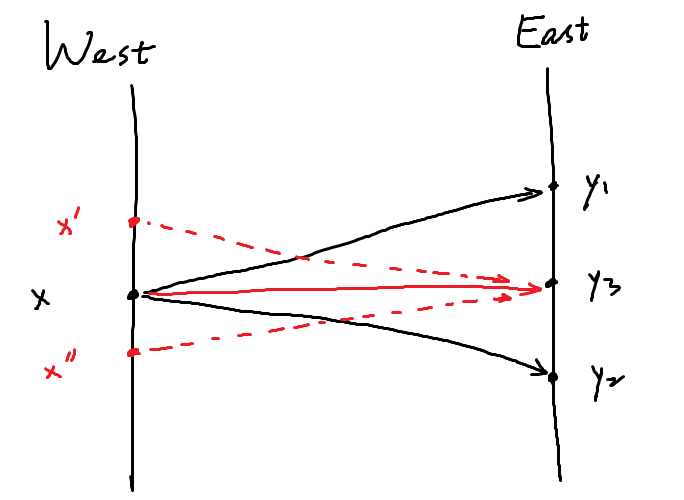
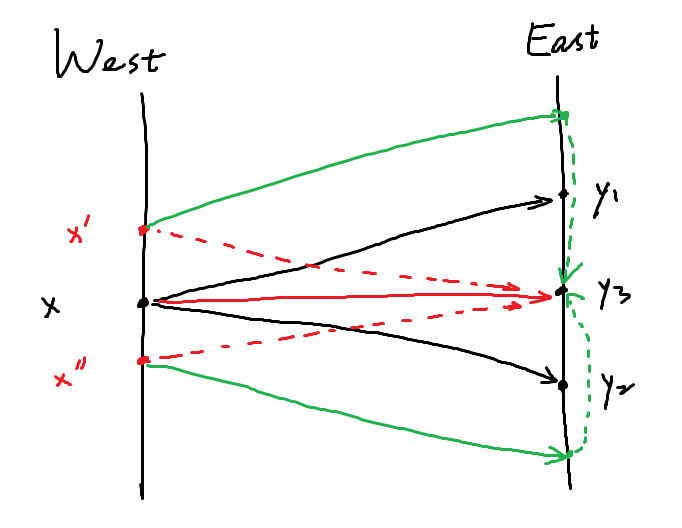
不失一般性，我们分析在北面的情况。如果 $x'$ 想要达到 $y_3$，在平面上势必要穿过 $x \rightsquigarrow y_1$ 的一条路径。但是，我们不能直接在 $x \rightsquigarrow y_1$ 的某个节点处经过，因为这样的话，$x$ 便也能达到 $y_3$ 了。所以我们最终的路径会与 $x \rightsquigarrow y_1$ 相交，且产生交点不在节点处。与题设矛盾，故 $y_3$ 对于 $x$ 必可达。

下图展示了两种不可能（虚线）的情况：

得到了这个结论，我们接下来描述一下算法思路：

从西海岸跑一遍 BFS 看东海岸哪些点是可达的，重新编号，复杂度 $O(n)$
从东海岸按照 $y$ 的值 从大到小 跑一遍 BFS 记录西海岸每个点能够到达的最大的 $y$
从东海岸按照 $y$ 的值 从小到大 跑一边 BFS 记录西海岸每个点能够到达的最小的 $y$
根据我们的结论就能计算出西海岸每个点的东海岸可达数目 $y_{\max} - y_{\min} + 1$

代码

// CEOI 2011 Traffic
// http://ceoi.inf.elte.hu/tasks-archive/
// https://oi.edu.pl/static/attachment/20110713/ceoi-2011.pdf
// https://www.luogu.com.cn/problem/P4700
#include <iostream>
#include <queue>
#include <algorithm>
#define int long long

using namespace std;

const int maxn = 3e5+5;
const int maxm = 2e6;

struct node { int x, y, ans[2]; } v[maxn];
struct edge { int to, next; } g[maxm], _g[maxm];
int ecnt = 2, _ecnt = 2, head[maxn], _head[maxn];

queue<int> q;
int vis[maxn];
int ans_index = 0;

int n, m, A, B;

int E[maxn], Ecnt = 0;
int W[maxn], Wcnt = 0;

bool cmp(int a, int b) {
    return v[a].y < v[b].y;
}

void add_edge(int u, int v) {
    g[ecnt] = (edge) {v, head[u]};
    head[u] = ecnt ++;
}

void _add_edge(int u, int v) {
    _g[_ecnt] = (edge) {v, _head[u]};
    _head[u] = _ecnt ++;
}

void bfs1() {
    for (int i = 1; i <= n; i ++)
        if (!v[i].x) {
            q.push(i);
            vis[i] = true;
        }
    while (!q.empty()) {
        int front = q.front();
        q.pop();
        for (int e = head[front]; e != 0; e = g[e].next) {
            int u = g[e].to;
            if (vis[u]) continue;
            q.push(u);
            vis[u] = true;
            if (v[u].x == A) E[++ Ecnt] = u;
        }
    }
    for (int i = 1; i <= n; i ++) vis[i] = false;
}

void bfs2(int u, int pi) {
    if (vis[u]) return;
    q.push(u);
    vis[u] = true;
    while (!q.empty()) {
        int front = q.front();
        q.pop();
        for (int e = _head[front]; e != 0; e = _g[e].next) {
            int vv = _g[e].to;
            if (vis[vv]) continue;
            q.push(vv);
            vis[vv] = true;
            if (!v[vv].x) v[vv].ans[ans_index] = pi;
        }
    }
}

signed main() {
    cin >> n >> m >> A >> B;
    for (int i = 1; i <= n; i ++)
        cin >> v[i].x >> v[i].y;
    int c, d, k;
    for (int i = 1; i <= m; i ++) {
        cin >> c >> d >> k;
        add_edge(c, d);
        _add_edge(d, c);
        if (k != 1) {
            add_edge(d, c);
            _add_edge(c, d);
        }
    }
    bfs1();
    sort(E + 1, E + 1 + Ecnt, cmp);

    for (int i = 1; i <= Ecnt; i ++)
        bfs2(E[i], i);
    ans_index ++;
    for (int i = 1; i <= n; i ++)
        vis[i] = false;
    for (int i = Ecnt; i >= 1; i --)
        bfs2(E[i], i);

    for (int i = 1; i <= n; i ++)
        if (!v[i].x)
            W[++ Wcnt] = i;
    sort(W + 1, W + 1 + Wcnt, cmp);

    for (int i = Wcnt; i >= 1; i --)
        if (!v[W[i]].ans[0] && !v[W[i]].ans[1]) cout << "0" << endl;
        else cout << (v[W[i]].ans[1] - v[W[i]].ans[0] + 1) << endl;
    return 0;
}