Preface

第三次做这题了...

顺便当成博客迁移了。下面的题解是高二上的时候写的，在 Hexo 的 blog，这里直接进行迁移：https://gyrojeff.moe/2020/09/18/P4568-JLOI2011-%E9%A3%9E%E8%A1%8C%E8%B7%AF%E7%BA%BF-%E5%88%86%E5%B1%82%E5%9B%BE%E6%9C%80%E7%9F%AD%E8%B7%AF/

题面

https://www.luogu.com.cn/problem/P4568

题解

由于可以有$k$次免费，这里构建分层图：

• 有$k+1$层完全一样的图
• 每条边在层与层之间单向连接，但是费用为0

那么这样构建的图的第$i$层的$t$点就是免费了$i - 1$次的最小费用。

方程：
$$
\text {ans} = \min _ {0 \leq i \leq k} \text {dis} [t_i]
$$

常见问题

• 如何防止从下面的层去上面？单向
• 如何建图？思考一下OpenCV当中的图像，其实他们的内存地址是连续的，所以我们可以把他们放在一个一维数组当中，只不过开了$n\times k$个点罢了。

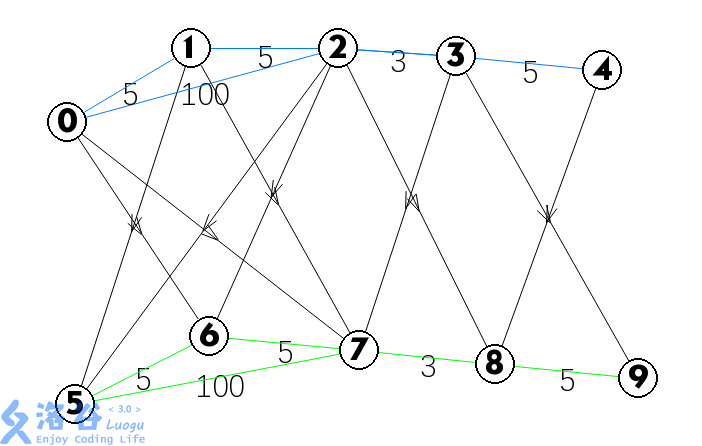
图片（Ref @SuperJvRuo）

代码

#include <iostream>
#include <queue>
#include <cstring>
#define int long long

using namespace std;

const int maxn = 1e4+5;
const int maxm = 5e4+5;
const int maxk = 15;

struct edge { int next, to, w; } g[(maxm * maxk) << 2];
int head[maxn * maxk], dis[maxn * maxk], vis[maxn * maxk], ecnt = 2, n, m, k, s, t;

void _add_edge(int u, int v, int w) {
    g[ecnt] = edge { head[u], v, w };
    head[u] = ecnt ++;
}

void add_edge(int u, int v, int w) {
    _add_edge(u, v, w);
    _add_edge(v, u, w);
}

void add_edge(int u, int v, int k, int w) {
    add_edge(k * n + u, k * n + v, w);
}

void add_edge(int u, int v, int k1, int k2, int w) {
    _add_edge(k1 * n + u, k2 * n + v, w);
    _add_edge(k1 * n + v, k2 * n + u, w);
}

struct node {
    int pos, dis;

    friend bool operator < (const node &a, const node &b) {
        return a.dis > b.dis;
    }
};

priority_queue<node> q;

void dijkstra() {
    memset(dis, 0x7f, sizeof(dis));
    dis[s] = 0;
    q.push(node { s, 0 });
    while (!q.empty()) {
        int u = q.top().pos; q.pop();
        if (vis[u]) continue;
        vis[u] = 1;
        for (int e = head[u]; e; e = g[e].next) {
            int v = g[e].to;
            if (vis[v]) continue;
            if (dis[v] > dis[u] + g[e].w) {
                dis[v] = dis[u] + g[e].w;
                q.push(node { v, dis[v] });
            }
        }
    }
}

signed main() {
    cin >> n >> m >> k >> s >> t;
    while (m --> 0) {
        int u, v, w; cin >> u >> v >> w;
        for (int i = 0; i <= k; i ++)
            add_edge(u, v, i, w);
        for (int i = 0; i < k; i ++)
            add_edge(u, v, i, i + 1, 0);
    }
    dijkstra();
    int ans = 8e18;
    for (int i = 0; i <= k; i ++)
        ans = min(ans, dis[t + i * n]);
    cout << ans << endl;
    return 0;
}