题面
https://www.luogu.com.cn/problem/P1363
题解
先说正解。
怎么样才能判断可以无限延伸呢?那就是如果存在一条路径
$$
P \rightsquigarrow P'
$$
其中 $P'$ 为任意一个虚幻棋盘中 $P$ 的对应点。
证明十分容易。
充分性证明:记坐标 $P$ 为 $P(x, y), 0 \leq x < n, 0 \leq y < m$。那么:
$$
P'(x + na, y + mb), a, b \in \mathbb Z, a,b 不同时为0
$$
所以根据假设存在下面的路径:
$$
P(x, y) \rightsquigarrow P(x + na, y + mb)
$$
则亦存在:
$$
P(x + na, y + mb) \rightsquigarrow P(x + 2na, y + 2mb)
$$
我们将路径记作下面这种映射:
$$
f(x, y) = (x + na, y + mb)
$$
故我们可以不断应用:
$$
f^{(t)}(x, y) = \underbrace{f(f(\cdots f}_{t}(x, y) \cdots)) = (x + tna, y + tmb)
$$
故
$$
\lim_{t \rightarrow \infty} f^{(t)}(x, y) = \begin{cases}
(\infty, \infty) & ab \neq 0 \\ (0, \infty) & a = 0 \\ (\infty, 0) & b = 0
\end{cases}
$$
必要性证明可以通过反证法证得:
向无穷远处延伸代表存在长度为无穷的路径。接下来应用反正:若存在长度为无穷的路径,且不存在形如题设的 $P \rightsquigarrow P'$ 的路径。
若不存在形如 $P \rightsquigarrow P'$ 的路径,那么路径长度必然是有限的,因为我们能够构造出来的路径都形如下式:
$$
S \rightsquigarrow T = S \rightsquigarrow A_1 \rightsquigarrow A_2 \rightsquigarrow \cdots \rightsquigarrow A_p \rightsquigarrow T
$$
其中等式右侧的每条路径都不存在中间点。我们不难发现集合 $A$ 是有限的,因为原棋盘是有限的,故 $|A \cup \{S, T\}| \leq nm$。故长度必然为有限,与长度为无限矛盾。证毕。
下面是一些错误结论:
错误结论 1:向上下左右各拓展一个棋盘,如果一个点被等价走到了两次,那么就可以到达无穷。
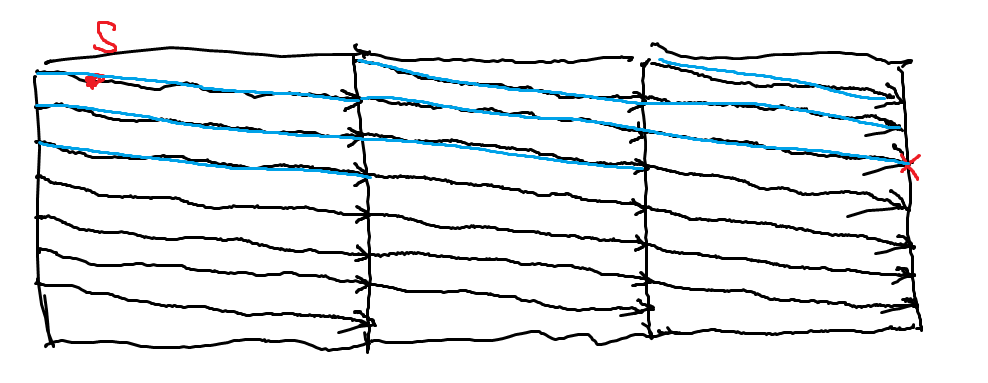
反例:
代码
#include <iostream>
#include <cstring>
using namespace std;
const int maxn = 1505;
const int dx[4] = {-1, 0, 0, 1};
const int dy[4] = {0, -1, 1, 0};
int n, m, sx, sy, vx[maxn][maxn], vy[maxn][maxn];
bool map[maxn][maxn], vis[maxn][maxn], ans;
void dfs(int x, int y, int lx, int ly) {
if (ans) return;
if (vis[x][y]) {
if (vx[x][y] != lx || vy[x][y] != ly) ans = 1;
return;
}
vis[x][y] = 1; vx[x][y] = lx; vy[x][y] = ly;
for (int i = 0; i < 4; i ++) {
int xx = (x + n + dx[i]) % n;
int yy = (y + m + dy[i]) % m;
int lxx = lx + dx[i], lyy = ly + dy[i];
if (map[xx][yy])
dfs(xx, yy, lxx, lyy);
}
}
int main() {
char in;
while (cin >> n >> m) {
for (int i = 0; i < n; i ++)
for (int j = 0; j < m; j ++) {
cin >> in;
map[i][j] = (in != '#');
if (in == 'S') sx = i, sy = j;
}
memset(vis, 0, sizeof(vis));
memset(vx, 0, sizeof(vx));
memset(vy, 0, sizeof(vy));
ans = 0;
dfs(sx, sy, sx, sy);
if (ans) cout << "Yes" << endl;
else cout << "No" << endl;
}
return 0;
}