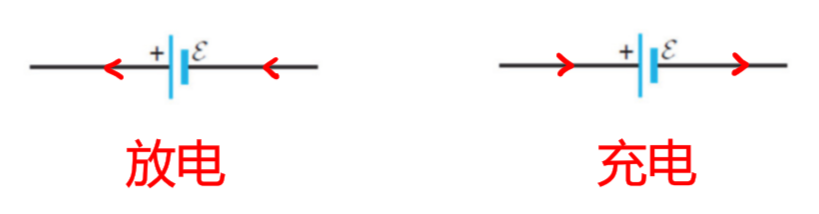考前自救 - AP M&E整理

Unit 1 - Electrostatics 静电学

1.1 Coulomb's Law 库仑定律

$$
F = k \frac {q_1 q_2}{r ^ 2}
$$

$$
k = \frac 1 {4 \pi \epsilon_0}
$$

1.2 Electric Field 电场

Definition:

$$
\vec E = \frac {\vec F} q
$$

$$
E = \frac F q = k \frac q {r ^ 2} = \frac 1 {4 \pi \epsilon_0} \frac q {r ^ 2}
$$

1.3 Gauss's Law 高斯定理

$$
\phi_E = \oint \vec E \cdot \mathrm d \vec A = \frac {q_{\text {enclose}}} {\epsilon_0}
$$

1.4 Gauss's Law 推论

两块平行金属板之间的电场：

$$
E = \frac {\sigma} {\epsilon_0}
$$

证明：

$$
\phi_E = \oint \vec E \cdot \mathrm d \vec A = EA = \frac {\sigma A} {\epsilon_0} \Rightarrow E = \frac {\sigma} {\epsilon_0}
$$

$k$的推导：用高斯定律计算点电荷的电场

$$
\phi_E = \oint \vec E \cdot \mathrm d \vec A = 4\pi r^2 E = \frac {q} {\epsilon_0} \Rightarrow E = \frac {1}{4\pi \epsilon_0} \frac {q} {r ^ 2}
$$

1.5 Electric Potential Energy 电势能

规定：无穷远处电势能为$0$

$$
U_{\infty} = 0
$$

这一点的电势能等于无穷远处到这一点的电势能变化量:

$$
U_{r} = \Delta U_{\infty \rightarrow r}
$$

证明:

$$
\Delta U_{\infty \rightarrow r} = U_r - U_{\infty} = U_r
$$

电势能变化量等于电场力做的功的相反数:

$$
\Delta U = -W_F
$$

根据上述关系求出电势能表达式:

$$
U_r = - \int _ {r} ^ {\infty} \vec F \cdot \mathrm d \vec r
$$

证明:

$$
U_r = \Delta U_{\infty \rightarrow r} = -W_{F: \infty \rightarrow r} = \int _ {r} ^ {\infty} \vec F \cdot \mathrm d \vec r
$$

点电荷的电势能公式:

$$
U_r = \frac {k q q_0} r
$$

证明:

$$
\begin{aligned}
U_r &= \int _ {r} ^ {\infty} \vec F \cdot \mathrm d \vec r \\
&= \int _ {r} ^ {\infty} \frac {k q q_0} {r ^ 2} \mathrm d r \\
&= \Big [ - \frac {k q q_0} {r} \Big ] _ r ^ \infty \\
&= \frac {k q q_0} {r}
\end{aligned}
$$

多个点电荷的电势能计算

$$
U = kq_0 \Big ( \frac {q_1} {r_1} + \frac {q_2} {r_2} + \frac {q_3} {r_3} + \cdots \Big )
$$

$$
U = kq_0 \sum _ i \frac {q_i} {r_i}
$$

1.6 Electric Potential 电势

定义式:

$$
V = \frac {U} {q_0}
$$

国内符号:

$$
E_p= \varphi q_0
$$

点电荷的电势公式:

$$
V = \frac {k q} {r}
$$

靠近负点电荷，电势为负

靠近正点电荷，电势为正

多个点电荷的电势能计算

$$
V = k \Big ( \frac {q_1} {r_1} + \frac {q_2} {r_2} + \frac {q_3} {r_3} + \cdots \Big )
$$

$$
V = k \sum _ i \frac {q_i} {r_i}
$$

1.7 电场与电势的重要关系

$$
E = -\frac {\mathrm d V} {\mathrm d r}
$$

$$
V = -\int E \mathrm dr
$$

场是势的微，势是场的积

顺电场方向，电势下降

逆电场方向，电势上升

沿电场线方向，电势下降得最快

证明:

$$
\begin{aligned}
-\int E \mathrm dr &= - \int \frac F q \mathrm dr \\
&= - \frac 1 q \int F \mathrm dr \\
&= - \frac 1 q W_F \\
&= - \frac 1 q (-U) = V
\end{aligned}
$$

Unit 2.1 - Conductors 导体

2.1.1 Electrostatic Equilibrium 静电平衡

在非电路当中，导体会达到静电平衡，无论有没有电场。 原因：

$$
\begin{aligned}
&内部有点电场的情况下 \\
&\downarrow \\
&电子快速移动 \\
&\downarrow \\
&产生反向电场 \\
&\downarrow \\
&逐渐达成静电平衡：内部电场为0
\end{aligned}
$$

2.1.2 静电平衡的几个重要结论

导体内部电场为 $0$，原因：静电平衡

导体中所有点电荷只能分布在内/外表面，原因：

$$
\begin{aligned}
&在内部任取高斯面 \\
&\downarrow \\
&因为电场为0 \\
&\downarrow \\
&\phi_E = \oint \vec E \cdot \mathrm d \vec A = 0 \\
&\downarrow \\
&\phi_E = \frac {q_{enc}} {\epsilon_0} = 0 \\
&\downarrow \\
&q_{enc} = 0 \\
&\downarrow \\
&内部无电荷
\end{aligned}
$$

内部电荷为$0$，上一条已经证明

导体是等势体，原因：

$$
\begin{aligned}
&因为电场处处为0 \\
&\downarrow \\
&\Delta V = - \int E \mathrm dr = 0 \\
&\downarrow \\
&等势体
\end{aligned}
$$

电场线垂直于导体表面，原因：

$$
\begin{aligned}
&\because 导体是等势体 \\
&\therefore 表面是等势面 \\
&又\because 电场线垂直于等势面 \\
&\therefore 电场线垂直于导体表面
\end{aligned}
$$

导体内部有空腔，无论空腔内的电荷如何移动位置，都只会改变内表面电荷分布，而不会改变外表面电荷分布，原因：

$$
\begin{aligned}
&\because 静电平衡 \\
&\therefore 导体内部不产生电场 \\
&\therefore 没有电场能够影响外表面电荷分布
\end{aligned}
$$

2.1.3 Electrostatic Shielding 静电屏蔽

静电屏蔽是指导体外壳对它的内部起到“保护”作用，使它的内部不受外部电场的影响。举例：法拉第笼 Faraday Cage

Unit 2.2 - Capacitors 电容器

2.2.1 Capacitor - 电容器

两个相互靠近的导体，中间夹一层不导电的绝缘介质，这就构成了电容器。当电容器的两个极板之间加上电压时，电容器就会储存电荷。电容器的电容量在数值上等于一个导电极板上的电荷量与两个极板之间的电压之比。电容器的电容量的基本单位是法拉(F)。在电路图中通常用字母C表示电容元件。

常用的电容器：两块平行金属板

2.2.2 Capacitance - 电容

Definition:

$$
C = \frac Q {\Delta V}
$$

Unit:

$$
1 \text F = 1 \frac {\text C} {\text V}
$$

注意：电容知识用来描述电容器的装电荷能力的，只和特定容器有关

注意：装电荷的上限和电容无关，只是电压拉的足够大之后，会击穿放电

2.2.3 平行金属板的电容公式

$$
C = \frac {\epsilon_0 A} {d}
$$

证明：

$$
C = \frac {Q} {\Delta V} = \frac {\sigma A} {Ed} = \frac {\sigma A} {\frac {\sigma} {\epsilon_0} d} = \frac {\epsilon_0A} {d}
$$

2.2.4 特殊的电容

并不是只有平行金属板才能作为电容器

单个金属球也能作为电容，另外一极在无穷远处的大地

2.2.5 电容中的电势能

电容能存能量

电容的能量存在在电场中，不在电极板上

表达式1:

$$
U = \frac {Q ^ 2} {2C}
$$

证明: 对于一个电容器，考虑每次将$\mathrm dQ$的电荷从负极板搬到正极板，每次的电势能增量就是$\mathrm dU = V\mathrm dQ = \displaystyle \frac Q C\mathrm dQ$，积分得到表达式：

$$
U = \int _ 0 ^ Q \frac 1 C Q \mathrm d Q = \frac {Q ^ 2} {2C}
$$

表达式2:

$$
U = \frac 1 2 C \Delta V ^ 2
$$

证明:

$$
U = \frac{Q ^ 2}{2C} = \frac {(C \Delta V) ^ 2} {2C} = \frac 1 2 C \Delta V ^ 2
$$

2.2.6 Energy Density 能量密度

对于电容器间的匀强场

$$
u = \text {Energy Density} = \frac {总能量} {总体积} = \frac {U} {V}
$$

对于平行金属板（匀强场）

$$
u = \displaystyle\frac {\frac {Q ^ 2} {2C}} {Ad} = \frac {\frac 1 2 C \Delta V ^ 2} {Ad}
$$

对于所有电容器 (不会证明)

$$
u = \frac 1 2 \epsilon_0 E ^ 2
$$

Unit 2.3 - Dielectrics 电介质

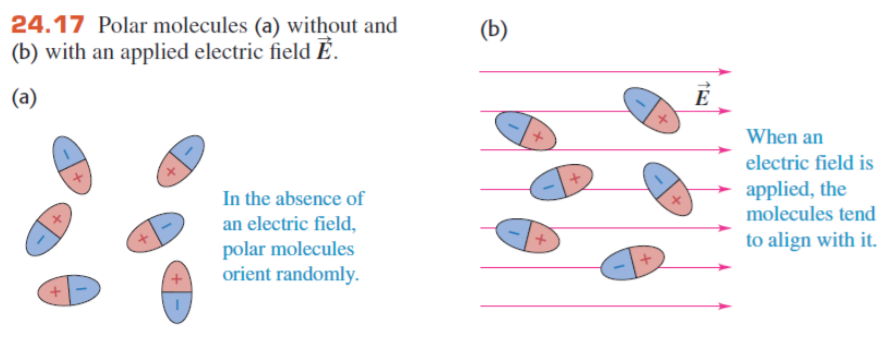
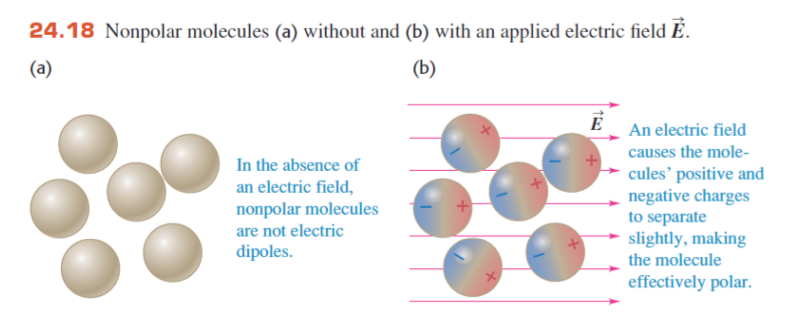
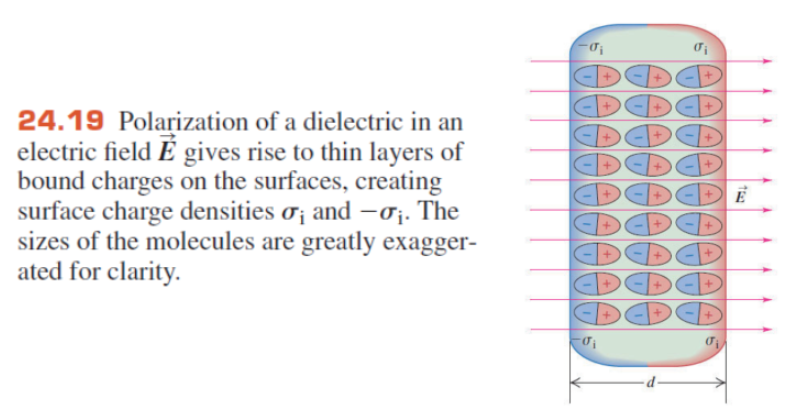
2.3.0 Dielectrics 电介质

上面几幅图简单介绍了电介质，记住一下要点：

$$
\begin{aligned}
&电场会让电极板间的分子（无论极性与否）极化 / 旋转 \\
&\downarrow \\
&产生相反方向的电场 \\
&\downarrow \\
&削弱原来方向的电场
\end{aligned}
$$

其中:

$$
E = \frac {E_0} {\kappa}
$$

2.3.1 Dielectric Constant 相对介电常量

Definition:

$$
\kappa = \frac C {C_0}
$$

常用计算式:

$$
C = \kappa C_0
$$

真空中$\kappa = 1$，其他时候$\kappa > 1$，所以电介质增强电容

2.3.2 几个介电常数

$$
\epsilon = \kappa \epsilon_0
$$

  • $\epsilon$: 绝对介电常数
  • $\kappa$: 相对介电常数
  • $\epsilon_0$: 真空介电常数

在有介电质的情况下，公式中可以将真空介电常数$\epsilon_0$替换为绝对介电常数$\epsilon$

2.3.3 有电介质的能量密度

$$
u = \frac 1 2 \kappa \epsilon_0 E ^ 2 = \frac 1 2 \epsilon E ^ 2
$$

Unit 3 - Electric Circuits 电路

3.1 Current 微观电流表达式

$$
I = qnAv_d
$$

  • $q$: 每个微粒所带的电荷
  • $n$: 单位体积内的微粒数
  • $A$: 导体的截面积
  • $v_d$: 电荷的移动速度

推导:

$$
I = \frac {\mathrm dQ} {\mathrm dt} = \frac {q \mathrm dN} {\mathrm dt} = \frac {qn\mathrm dV} {\mathrm dt} = \frac {qnA\mathrm ds} {\mathrm dt} = qnAv_d
$$

3.2 Current Density 电流密度

$$
J = \frac I A
$$

$$
J = \frac I A = nqv_d
$$

3.3 Resistivity 电阻率

$$
\rho = \frac E J
$$

单位：$\Omega \cdot m$

电阻率只与材料有关，是微观意义上的电阻，这也是微观的欧姆定律

3.4 电阻与电阻率的关系

$$
R = \rho \frac d A
$$

证明: 根据欧姆定律

$$
R = \frac V I = \frac {E d} {J A} = \rho \frac d A
$$

3.5 温度对电阻(率)的影响

$$
\rho (T) = \rho _ 0 [1 + \alpha (T - T_0)]
$$

$$
R (T) = R _ 0 [1 + \alpha (T - T_0)]
$$

其中$\alpha$理解为每升高$1$开尔文，$\rho$升高的百分比

3.6 Electric Energy 电能

$$
U = VIt
$$

推导:

$$
U = \int \mathrm dU = \int V \mathrm dQ = \int V I \mathrm dt = VIt
$$

3.7 电热 焦耳定律

$$
Q = I ^ 2 R t
$$

3.8 Electric Power 电功

$$
P = VI
$$

3.9 Ohm's Law在能量上的体现

Ohmic:

$$
VI = I ^ 2 R
$$

Nonohmic:

$$
VI > I ^ 2 R
$$

3.10 Electromotive Force (emf) 电动势

将$1C$电荷从负极移动到正极所需要的能量:

$$
\varepsilon = \frac U q
$$

3.11 Series 串联电路

$$
I_1 = I_2 = I_3 = \cdots
$$

$$
V = V_1 + V_2 + V_3 + \cdots = \sum_i V_i
$$

$$
R = R_1 + R_2 + R_3 + \cdots = \sum_i R_i
$$

3.12 Parallel 并联电路

$$
I = I_1 + I_2 + I_3 + \cdots = \sum_i I_i
$$

$$
V = V_1 = V_2 = V_3 = \cdots
$$

$$
\frac 1 R = \frac 1 {R_1} + \frac 1 {R_2} + \frac 1 {R_3} + \cdots = \sum_i \frac 1 {R_i}
$$

3.13 非理想电源

$$
\varepsilon = Ir + V_{ab}
$$

  • $I$: 电流
  • $r$: 内阻
  • $V_{ab}$: 路端电压
  • $\varepsilon$: 电动势

3.14 电池的充放电

充电功率:

$$
P = \varepsilon I
$$

有内阻的情况:

$$
P = \varepsilon I + I^2 r
$$

3.15 基尔霍夫定律

3.15.1 Junction Rule

基尔霍夫第一定律: 节点定律 Junction Rule

节点：电流分叉的地方

$$
I_{in} = I_{out}
$$

若规定$I_{in}$为正，$I_{out}$为负，则：

$$
\sum I = 0
$$

3.15.2 Loop Rule

基尔霍夫第二定律: 环定律 Loop Rule

$$
\sum V = 0
$$

应用技巧：

  1. 找到一个环，规定方向
  2. 对于在环上用电器，若环的方向与电流方向相同，电势下降，反之上升
  3. 电源: 正极 $\rightarrow$ 负极，电势下降，理解的话可以考虑正极电势比负极高

3.16 改装电表

  1. 改装成电流表：并联电阻分担电流
  2. 改装成电压表：串联电阻分担电压

注意：电压表和电流表其实一样，就是乘除自身电阻的事，不必纠结。

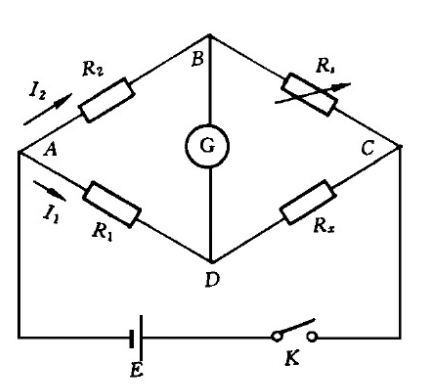
3.17 Wheatstone Bride 惠斯通电桥

调节BC间的滑动变阻器$R_s$当B、D两点间电势差为$0$，即灵敏电流计示数为零时，下式成立：

$$
\frac {R_2} {R_1} = \frac {R_s} {R_x}
$$

则可以求出未知阻值的电阻$R_x$:

$$
R_x = R_s \frac {R_1} {R_2}
$$

3.18 电容串联的等效电容

条件：事先不带电！！！！

$$
\frac 1 C = \frac 1 {C_1} + \frac 1 {C_2} + \cdots = \sum_i \frac 1 {C_i}
$$

证明：

$$
\begin{aligned}
&\because 事先不带电 \\
&\therefore 中间的由导线相连的两块板的电荷应该异号等大
\end{aligned}
$$

又因为串联电路，所以

$$
V = V_1 + V_2 + \cdots
$$

$$
\frac Q C = \frac Q {C_1} + \frac Q {C_2} + \cdots
$$

得证

3.19 电容并联的等效电容

$$
C = C_1 + C_2 + \cdots = \sum_i C_i
$$

证明：并联电路：

$$
C = \frac Q V = \frac {Q_1 + Q_2 + \cdots} V = C_1 + C_2 + \cdots
$$

3.20 串联分压，并联分流

串联：

$$
\frac {R_1} {R_2} = \frac {V_1} {V_2}
$$

并联：

$$
\frac {R_1} {R_2} = \frac {I_2} {I_1}
$$

3.21 电容和电压关系

$$
\frac {C_1} {C_2} = \frac {V_2} {V_1}
$$

3.22 RC电路

电阻和电容串联的电路叫做RC电路：

3.23 Time Constant - RC电路中得时间常数

$$
\tau = RC
$$

时间常数越大，充电 / 放电时间越大。充电 / 放电时间和时间常数成正比。

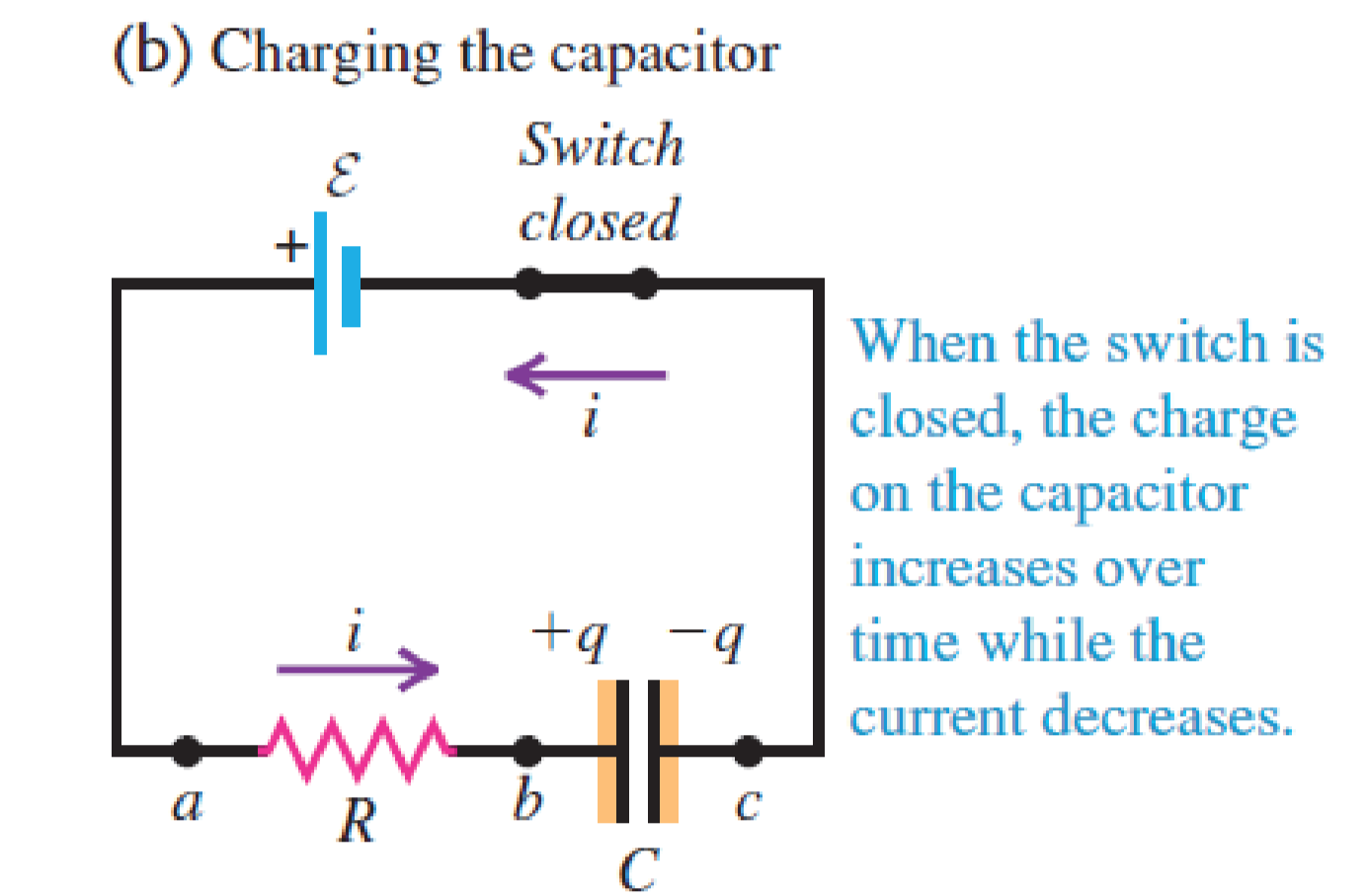
3.24 RC电路充电

规定电流方向（随意，便于列方程）:

根据基尔霍夫的节点定律列方程：电极板上的电荷变化率就是电流大小：

$$
i = \frac {\mathrm dq} {\mathrm dt}
$$

根据基尔霍夫的环定理列方程：

$$
\varepsilon - iR - \frac q C = 0
$$

解微分方程，得：

$$
q = \varepsilon C (1 - e ^ {- \frac t {RC}})
$$

令$Q_f = \varepsilon C$

$$
q = Q_f (1 - e ^ {- \frac t \tau})
$$

$$
i = \frac \varepsilon R e ^ {-\frac t \tau} = I_0 e ^ {-\frac t \tau}
$$

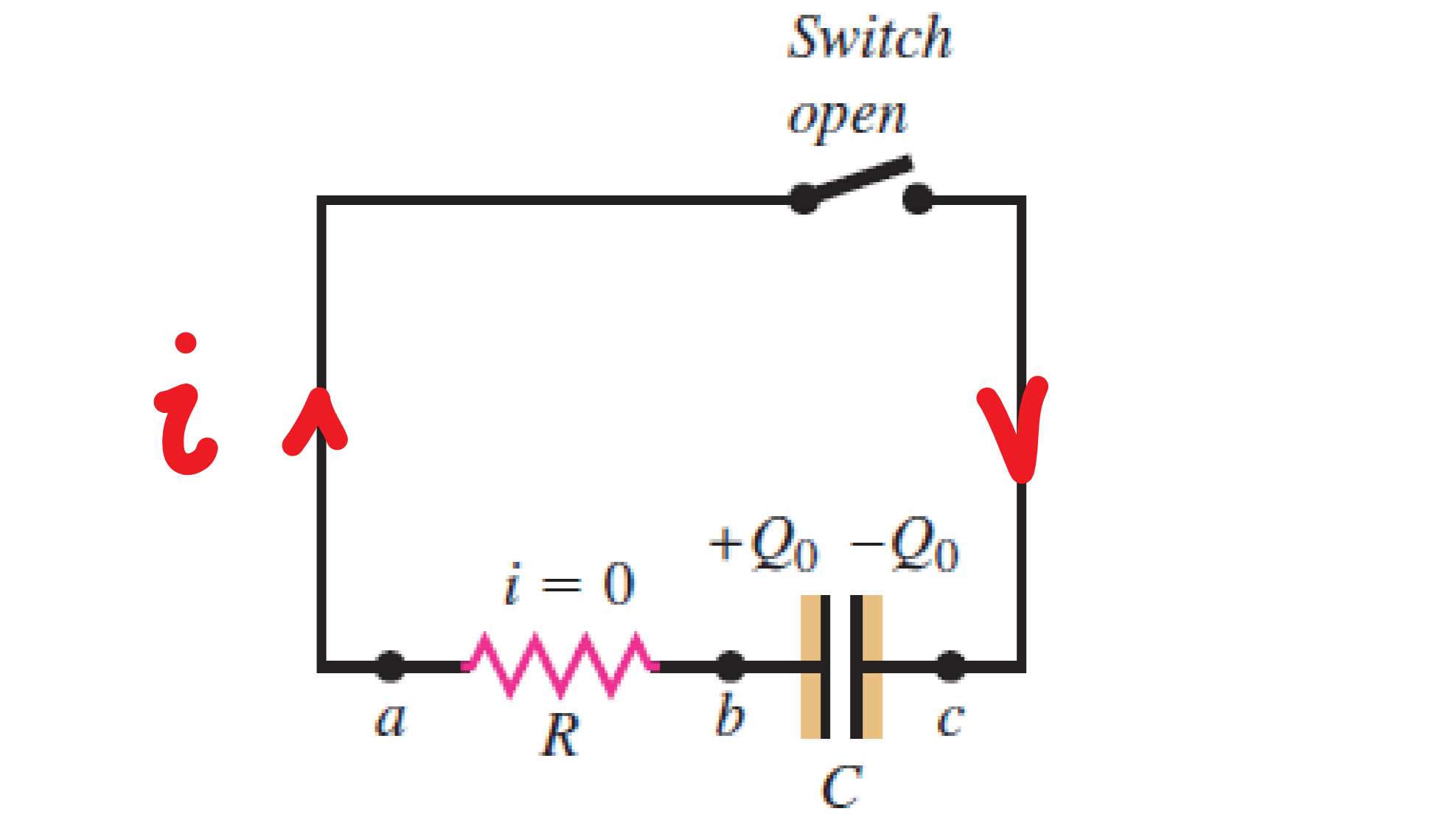
3.25 RC电路放电

规定电流方向（随意，便于列方程）:

根据基尔霍夫的节点定律列方程：电极板上的电荷变化率的相反数就是电流大小：

$$
i = - \frac {\mathrm dq} {\mathrm dt}
$$

根据基尔霍夫的环定理列方程：

$$
+\frac q C - iR = 0
$$

解微分方程，得：

$$
q = Q_0 e ^ {- \frac t {RC}} = Q_0 e ^ {- \frac t \tau}
$$

$$
i = \frac {Q_0} {RC} e ^ {- \frac t {RC}} = I_0 e ^ {- \frac t \tau}
$$

这两个图像很好脑补，就是指数衰减，这里就不画了。

Unit 4 磁场 Magnetic Fields

4.1 洛伦兹力 Lorentz Force

$$
F = q \cdot \vec v \times \vec B
$$

4.2 安培力 Ampere's Force

$$
F = I \cdot \vec L \times \vec B
$$

4.3 无限长直导线的磁场

$$
B = \frac {\mu_0} {2\pi} \frac I r
$$

4.4 Biot-Savart Law 毕奥-萨伐尔定律

$$
\mathrm d \vec B = \frac {\mu_0} {4 \pi} \frac {I (\mathrm d \vec \ell \times \hat r)} {r^2}
$$

  • 其中：$\mathrm d \ell$为电流元

4.5 Ampere's Law 安培环路定理

$$
\oint \vec B \cdot \mathrm d \vec l = \mu_0 I
$$

注：这里是点乘，可以理解为投影和分量

解题步骤:

  1. 先确定出环路的方向
  2. 应用计算

题目要求画的安培环路要画方向！！

4.6 无限长螺线管的磁场

内:

$$
B = \mu_0 n I
$$

外:

$$
B = 0
$$

如何推导？取一个到无穷远的安培环路，那里的磁感应强度为0

Unit 5 Electromagnetism 电磁

5.1 动生电动势 Motional EMF

$$
\varepsilon = Blv
$$

条件：

$$
v \perp l \perp B
$$

5.2 动生电动势的推导（1）

$$
\begin{aligned}
&导线中的电子收到洛伦兹力 \\
&\downarrow \\
&电子移动，在导线两端聚集 \\
&\downarrow \\
&产生电场 \\
&\downarrow \\
&电子同时受到电场力和洛伦兹力，力平衡
\end{aligned}
$$

$$
qE = qvB
$$

$$
E = vB
$$

$$
\varepsilon = vBl
$$

5.3 这里洛伦兹到底做不做功？

  • 洛伦兹力的合力不做功
  • 洛伦兹力在导线方向的分力做正功
  • 洛伦兹力在运动方向的分力做负功

5.4 一个值得思考的情况

5.5 磁通量 - Magneic Flux

$$
\Phi_B = \int B_\perp \mathrm dA = \int B \cos \Phi \mathrm d A = \int \vec B \cdot \mathrm {\vec A}
$$

5.6 闭合面的磁通量为0

因为没有“磁荷”，而且磁感线闭合

$$
\oint \vec B \cdot \mathrm d \vec A = 0
$$

5.7 法拉第定律 - Faraday's Law

$$
\varepsilon = - \frac {\mathrm d \Phi} {\mathrm d t}
$$

5.8 楞次定律 - Lenz's Law

感应电流具有这样的方向，即感应电流的磁场总要阻碍引起感应电流的磁通量的变化。

5.9 感生电场

电场力让电荷绕一圈做的功，就是感生电动势的功：

$$
qE \cdot 2\pi r = q \varepsilon
$$

所以

$$
E \cdot 2\pi r = \varepsilon = -\frac {\mathrm d \Phi} {\mathrm d t}
$$

又因为电势就是电场的积，所以：

$$
\oint \vec E \cdot \mathrm d \vec l = E \cdot 2 \pi r = \varepsilon = - \frac {\mathrm d \Phi} {\mathrm d t}
$$

5.10 非静电场

感生电场是非静电场，场源在变。

5.11 电感 - Inductance

$$
\varepsilon = - L \frac {\mathrm d I}{\mathrm d t}
$$

5.12 电感的性质

  1. 在电流不变的时候，电感就是导线
  2. 顺电流方向：
    $$\Delta V = -L \frac {\mathrm d i } {\mathrm d t}$$
  3. 经过电感的电流不能发生突变，因为电流的变化不可能突变：
    $$
    \frac {\mathrm d i} {\mathrm d t} = \infty \Rightarrow \varepsilon = \infty
    $$

5.13 磁能

让电感电流从0增加到$I$的能量就是磁能：

$$
U = \frac 1 2 L I^2
$$

推导：电感某时刻的功率是$\displaystyle P = \varepsilon i = -L\frac {\mathrm d i } {\mathrm d t}i$, 对时间积分再求负数就是储存下来的能量：

$$
U = -\int_0^I -L\frac {\mathrm d i } {\mathrm d t}i\mathrm dt = - \int_0^I -Li\mathrm d i = \frac 1 2 L I ^ 2
$$

5.14 RL电路

列方程方法：基尔霍夫。和电容不同，这次只需要列一个基尔霍夫就行了。比如：

$$
+\varepsilon -iR - L \frac{\mathrm d i} {\mathrm dt} = 0
$$

5.15 RL电路的充电

$$
i = I_f(1-e^{-\frac t \tau}) = \frac \varepsilon R (1 - e^{-\frac t {L / R}})
$$

$$
\frac {\mathrm di} {\mathrm dt} = \frac {\varepsilon} L e ^ {-\frac t \tau} =\frac {\varepsilon} L e ^ {-\frac t {L/R}}
$$

能量守恒 (最后那个部分是磁能的功率（就是积分之前）)：

$$
\varepsilon i = i^2 R + Li\frac {\mathrm d i} {\mathrm dt}
$$

5.16 RL电路的放电

$$
i = I_0 e^{-\frac t \tau} = I_0 e^{-\frac t {L / R}}
$$

$$
\frac {\mathrm di} {\mathrm dt} = -\frac {I_0R} Le^{-\frac t\tau}
$$

5.17 LC电路

和简谐振动对比：

$$
U_s + K = \text {constant} \Leftrightarrow U_L + U_C = \text {constant}
$$

$$
U_s = \frac 1 2 k \Delta x ^ 2 \Leftrightarrow U_C = \frac 1 2 \frac 1 C q ^ 2
$$

$$
K = \frac 1 2 m v ^ 2 \Leftrightarrow U_L = \frac 1 2 L i ^ 2
$$

$$
v = \frac {\mathrm d \Delta x} {\mathrm d t} \Leftrightarrow i = \frac {\mathrm d q} {\mathrm d t}
$$

$$
-k \Delta x = m \frac {\mathrm d v}{\mathrm d t} \Leftrightarrow -\frac 1 C q = L \frac{\mathrm di} {\mathrm dt}
$$

其中，最后一个方程是基尔霍夫。

所以，我们可以得到周期：

$$
T = 2\pi \sqrt \frac {L} {\frac 1 C} = 2\pi \sqrt {LC}
$$

5.18 麦克斯韦方程组 - Maxwell's Equation

  1. 电场的高斯定理
    $$
    \oint \vec E \cdot \mathrm d \vec A = \frac {q_{\text{enclosed}}} {\epsilon_0}
    $$
  2. 磁场的高斯定理
    $$
    \oint \vec B \cdot \mathrm d \vec A = 0
    $$
  3. 法拉第定律（然后电场的积分也是电动势）：
    $$
    \varepsilon = - \frac {\mathrm d \Phi_B} {\mathrm d t} = \oint \vec E \cdot \mathrm d \vec l
    $$
  4. 安培麦克斯韦方程（最后一项是麦克斯韦加上去的，因为变化的电场也能产生磁场）：
    $$
    \oint \vec B \cdot \mathrm d \vec l = \mu_0 I + \mu_0 \epsilon_0 \frac {\mathrm d \Phi_E} {\mathrm d t}
    $$

0. 零散知识点

尖端放电

越尖锐的地方，电荷越容易聚集，越容易放电

最后修改：2021 年 06 月 07 日 12 : 00 PM
© 允许规范转载
真的不买杯奶茶嘛....qwq