Preface
这块内容比较搞脑子,这里举一个较为简单的参数复用的例子来说明。基础内容请看:
https://zh-v2.d2l.ai/chapter_multilayer-perceptrons/backprop.html
回顾偏导数的链式法则
对于
$$
u = g(f_1(x_1, x_2, \cdots, x_n), f_2(x_1, x_2, \cdots, x_n), \cdots, f_m(x_1, x_2, \cdots, x_n))
$$
而言
$$
\frac{\partial u}{\partial x_j} = \sum_{i = 1} ^ m \frac {\partial g} {\partial f_i} \frac {\partial f_i} {\partial x_j}
$$
我们不妨将链式求导写成雅可比矩阵,更加通俗易懂:
$$
\left(\begin{array}{cccc}
\frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}} & \cdots & \frac{\partial u_{1}}{\partial x_{n}} \\
\frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} & \cdots & \frac{\partial u_{2}}{\partial x_{n}} \\
\cdots & \cdots & \cdots & \cdots \\
\frac{\partial u_{p}}{\partial x_{1}} & \frac{\partial u_{p}}{\partial x_{2}} & \cdots & \frac{\partial u_{p}}{\partial x_{n}}
\end{array}\right)=\left(\begin{array}{cccc}
\frac{\partial g_{1}}{\partial y_{1}} & \frac{\partial g_{1}}{\partial y_{2}} & \cdots & \frac{\partial g_{1}}{\partial y_{m}} \\
\frac{\partial g_{2}}{\partial y_{1}} & \frac{\partial g_{2}}{\partial y_{2}} & \cdots & \frac{\partial g_{2}}{\partial y_{m}} \\
\cdots & \cdots & \cdots & \cdots \\
\frac{\partial g_{p}}{\partial y_{1}} & \frac{\partial g_{p}}{\partial y_{2}} & \cdots & \frac{\partial g_{p}}{\partial y_{m}}
\end{array}\right)\left(\begin{array}{cccc}
\frac{\partial f_{1}}{\partial x_{1}} & \frac{\partial f_{1}}{\partial x_{2}} & \cdots & \frac{\partial f_{1}}{\partial x_{n}} \\
\frac{\partial f_{2}}{\partial x_{1}} & \frac{\partial f_{2}}{\partial x_{2}} & \cdots & \frac{\partial f_{2}}{\partial x_{n}} \\
\cdots & \cdots & \cdots & \cdots \\
\frac{\partial f_{m}}{\partial x_{1}} & \frac{\partial f_{m}}{\partial x_{2}} & \cdots & \frac{\partial f_{m}}{\partial x_{n}}
\end{array}\right)
$$
参数复用的例子
假设我们现在有如下的简单方程 (略去了激活函数来方便验证):
$$
A_1 = W x
$$
$$
Z_1 = A_1 + b_1
$$
$$
A_2 = W Z_1
$$
$$
Z_2 = A_2 + b_2
$$
这个过程中,$W$ 被用到了两次。思考一下在自动求导的过程中如果要求 $\displaystyle \frac{\partial Z_2}{\partial W}$ 会发生什么。
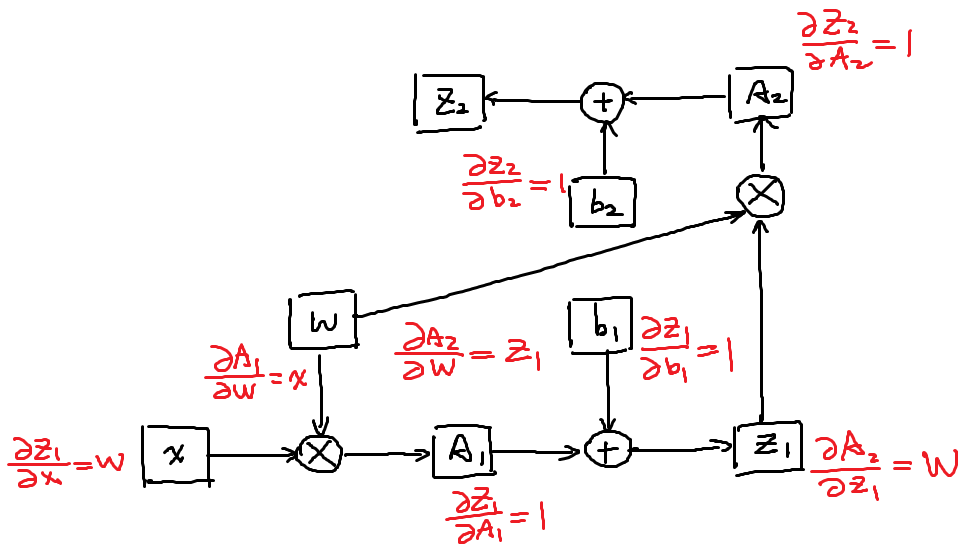
我们不妨先绘制出计算图
标出每一步的导数:
我们来看 $W$:
$$
\frac{\partial Z_2}{\partial W} = \frac {\partial Z_2}{\partial A_2} \left ( \frac {\partial A_2} {\partial W} + \frac {\partial A_2}{\partial Z_1} \frac {\partial Z_1}{\partial A_1} \frac {\partial A_1} {\partial W} \right )
$$
注意:整个过程中,我们不断地在定义多元函数,才能这么做:
$$
A_1 = W x = F_1(W, x)
$$
$$
Z_1 = A_1 + b_1 = F_2(A_1, b_1)
$$
$$
A_2 = W Z_1 = F_3(W, Z_1)
$$
$$
Z_2 = A_2 + b_2 = F_4(A_2, b_2)
$$
所以我们使用偏导的链式法则救不会出错。
参数复用的好处
共享参数通常可以节省内存,并在以下方面具有特定的好处:
- 对于图像识别中的CNN,共享参数使网络能够在图像中的任何地方而不是仅在某个区域中查找给定的功能。
- 对于RNN,它在序列的各个时间步之间共享参数,因此可以很好地推广到不同序列长度的示例。
- 对于自动编码器,编码器和解码器共享参数。 在具有线性激活的单层自动编码器中,共享权重会在权重矩阵的不同隐藏层之间强制正交。
Reference
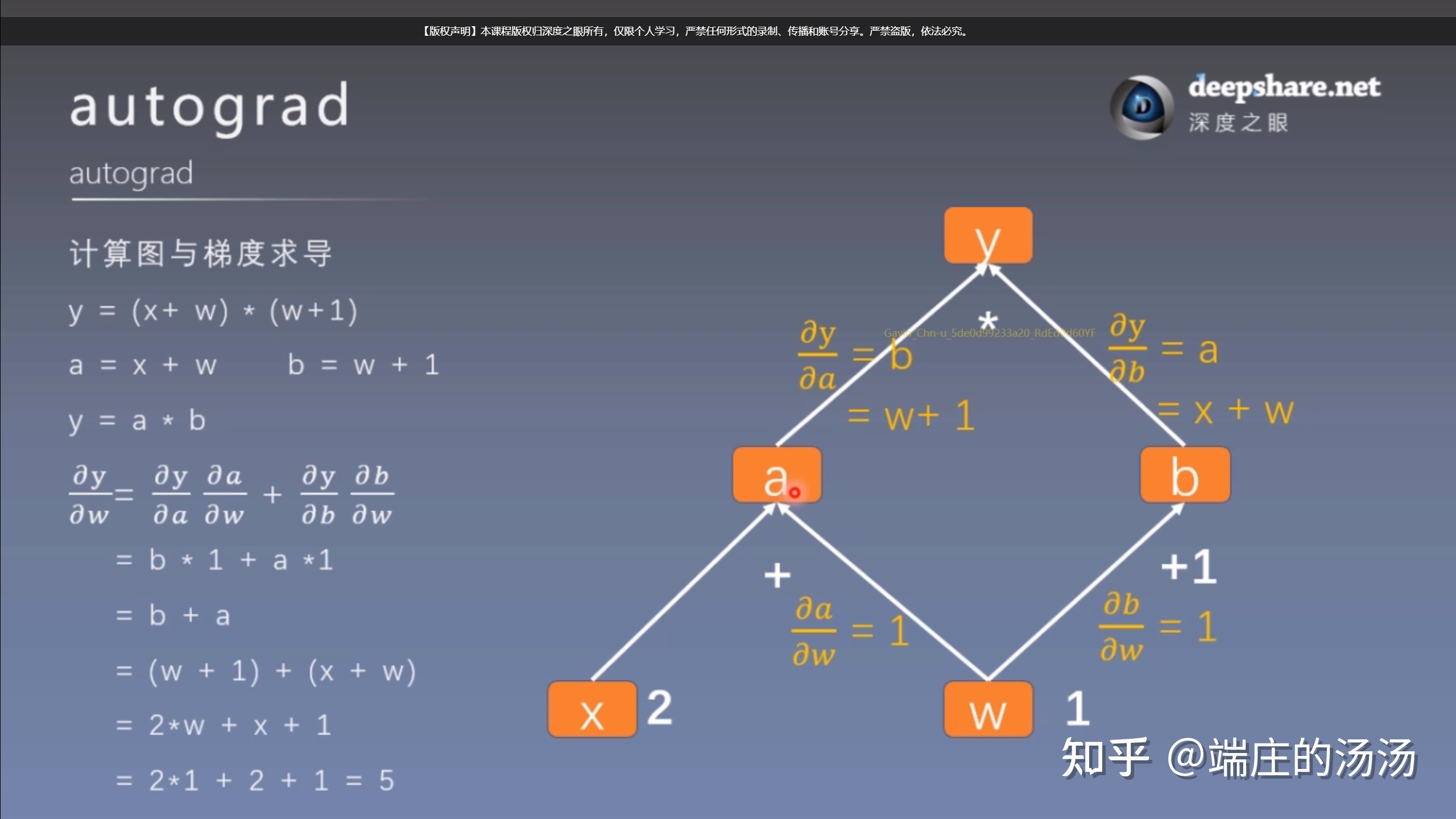
这张图让人醍醐灌顶: