最近在和汉化组合作，做漫画汉化自动化的相关事项，所以花了一个晚上研究这个东西，收获颇丰。这里主要介绍当时想出来的 重合度优先 模型，虽然现在已经不用了，但是十分有趣。

中文版是初稿，很多地方不太准确，不再仔细推敲了，如果有疑惑以英文版为准，其是我申请 MIT 时写的 Portfolio 的版本，做过勘误。

注意：其实这就是优化 $IoU$ (Intersection over Union), 只不过当时不知道这个词。

English Version

Current Exploration of Text Auto Layout Framework

I did several explorations about text auto layout framework, and am still actively researching for better methods. Here, I will introduce a method I proposed (though its performance didn't reach my expectation), Overlapping Oriented Model.

Prerequisite

• Text flow direction is either horizontal or vertical, other situations will not be considered.
• In the following part, it is assumed that the text is arranged vertically. It is similar for horizontal cases, I will not discuss here.
• Index starts from zero
• The target language of auto layout framework is Chinese, which
  flows mostly vertically in comics and its characters are full-width
  characters.

Main Idea

• Process the original image and obtain the expression of original text area
• By establishing a series of parameters and a region calculation model, the typesetting region can be calculated by parameters
• A function is established to calculate the overlapping degree between the generated typesetting area and the original text area
• Set the initial parameters, and maximize the function which calculates the overlapping degree.

Image Processing

Suppose we can turn the text blocks in the original image into black
areas through multiple manipulations such as erosion and dilation. Denote
the point set composed of these points as $T$.

Discuss a portion of text in an image. Suppose that we can process the
text into black blocks through multiple steps such as erosion, dilation,
and binarization, and denote the point set of these points as $T$.
Scan the point set $T$ column by column, and denote the subset of
points in each column as $T_i$. Introducing the hyperparameter
$\lambda$, such that, for each $T_i$, if

$$|T_i|<\lambda(\max{T_i}-\min{T_i})$$

then $T_i$ is rounded off from $T$, i.e.

$$T:=T-T_i$$

After the above step, we are able to obtain a roughly accurate point set
$T$ of text positions, and in order to compute other functions
conveniently, we may assume that it is a convex graph in the
longitudinal direction, and then represent it as a point set in the form
of

$$T^*=[(y_{0s},y_{0e}),(y_{1s},y_{e}),... ,(y_{ns},y_{ne})]$$

The meaning of the above equation is to describe it in the form of a set
of columns, and each column can be expressed in the form of beginning
and ending vertical coordinates (because we assume that it is a convex
graph). If the text is horizontal, we would only need to assume that it
is a convex graph in the horizontal direction, and then a similar
equation can be obtained, which will not be discussed here.

Note that,

• If a column does not have any pixels, then the expression for that
  column is written as $(y_{\max},0)$. This is done because it is
  convenient to make comparisons in this form.

Region Calculation Function

The typesetting region is determined by a lot of factors. Here, I picked
some of the most important factors:

• Starting horizontal coordinate (rightmost horizontal coordinate of the
  text) $x$
• Starting vertical coordinate (upmost vertical coordinate of the text)
  $y$
• Text wrapping position
• Font size $l_f$, here we take it as the number of pixels occupied by
  each \textbf{Full-width Character}
• Text spacing $d$, here we take it as the number of pixels in the gap
  between two columns of texts

Next, I will first discuss the text wrapping position, which can be
expressed in many forms:

• A multidimensional vector, recording how many words each column has
• A multidimensional vector, recording the location of each separation
• A One-Hot multidimensional vector, recording whether there is a
  separation between each two neighboring characters

For the first expression, there is a constraint that the sum of the
values of all dimensions of the vector must be the text length, i.e.
$\sum_i{w_i}=l_t$, which increases the difficulty of calculation. For
the third expression, it is very difficult to calculate the text length
directly from the expression itself. As a result, I finally chose the
second expression to record the location of the segmentation, and
$[c_{i-1},c_i)$ represents the $i^\text{th}$ segmentation interval.

After deciding the encoding method, we will discuss how to enumerate the
text separation cases. It is not difficult to find that the line break
cases can be enumerated in finite time. However, if separation can
happen between all characters, then there are $2^{m-1}$ in character
cases, assuming that the total number of characters is $m$, which is
undoubtedly catastrophic. After all, this is already exponential
complexity.

Therefore, we need to add certain constraints, e.g.

• the number of columns $k$
• the number of longest characters in the column $m'$

Based on the above two constraints, we can give an enumeration of all
possible cases, denoted as $C$.

Note: Since sometimes line breaks are needed due to pauses and semantic
splits, $\vec{c}$ may be given by the user, or the user may give
partial splitting results.

To summarize, we can now build the region calculation function with
$x,y,l_f,d,\vec{c}$, which are all parameters that need to be
optimized except for $\vec{c}$. Denote

$$\vec\theta=(x,y,l_f,d)$$

as the parameters. Let the region calculation function be

$$A(\vec\theta,\vec{c})$$

The result of this function has the same dimensions as $\vec{c}$,
recording the vertical starting and ending positions of each column:

$$A(\vec\theta,\vec{c})_i=(x-i\times{(l_f+d)},y,y+\sum_{a=c_{i-1}}^{c_i-1}f(t(a)))$$

Note that,

• We introduced $f(t)$ and $t(a)$ to represent the pixel size
  function for the character $t$ and the character $t$ at position
  $a$, respectively, in order to solve the cases when there are
  non-full-width characters (e.g. space, commas).
• For some substrings, e.g. English words, special symbols, and all
  other cases where the character length exceeds $1$ but the final
  rendering length is $1$, they are preprocessed and replaced with
  UTF-8 placeholders in the calculation, e.g.
  \u0000, \u0001, etc.

Here is an example,

Extending $A$ to a matrix $A^*$ of the entire image size length to
obtain a result similar to $T^*$:

$$\forall{i\in[0,|\vec{c}|)},\forall{j\in{[0,l_f)}},k=x-i\times{(l_f+d)} \Rightarrow A^*(\vec\theta,\vec{c})_{k-j}=(y,y+\sum_{a=c_{i-1}}^{c_i-1}f(t(a)))$$

In other cases,

$$A^*(\vec\theta,\vec{c})_p=(0,0)$$

Calculate the Overlapping Degree

To define the degree of overlap between the original region $T^*$ and
the computed typesetting region $A^*$, define the overlap metric,

$$L(\vec\theta,\vec{c})=\displaystyle\frac{A^*\cap{T^*}}{A^*\cup{T^*}}=\sum_i\frac{A_i^*\cap{T_i^*}}{A_i^*\cup{T_i^*}}$$

Now define the $\cap,\cup$ operations between $(a,b),(c,d)$: when
$d-a>0,b-c>0$ hold simultaneously, and $(a,b),(c,d)$ are legal
intervals, ($(y_{\max{}},0)$ at initialization is an illegal interval),

$$(a,b)\cap(c,d)=\min(d-a,b-c)$$

$$(a,b)\cup(c,d)=\max(d-a,b-c)=(b-a)+(d-c)+(a,b)\cap(c,d)$$

Otherwise,

$$(a,b)\cap(c,d)=0$$

$$(a,b)\cup(c,d)=(b-a)+(d-c)$$

To summarize, we are calculating the ratio of the intersection and sum
of two regions to calculate the degree of overlap, and we want this
value $L$ to be as close to $1$ as possible.

Maximize the Overlapping Degree

Since $L$ satisfies $0\leq{L}\leq1$, we can use gradient ascent to
maximize it,

$$\vec\theta:=\vec\theta+\alpha\frac{\partial{L(\vec\theta,\vec{c})}}{\partial{\vec\theta}}$$

in which the hyperparameter $\alpha$ is the learning rate.

Experiment

See
oom/notebook.ipynb.
Here is an example,

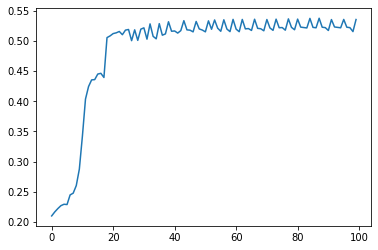
• epoch: 100
• L: 55%
• time: 27.7 s
• alpha: 15

Accuracy:

Result:

Conclusion

The initial goal was achieved, but choosing overlapping degree as an
indicator cannot fulfill the requirement in all scenarios. As a result,
in the future, I will explore other ways to solve this problem.

中文版

[DEPRECATED] 2021/09/24 OOM (Overlaping Oriented Model)

• 本模型仅讨论文本块为水平或者竖直的情况，更复杂的情况将在以后进行讨论
• 下文中假设文本为竖排，横排情况类似，不做过多讨论
• 下标一般从0开始

主要思想

• 首先对于原图进行处理，得到便于计算的原文字区域表达
• 通过建立一系列参数和一个区域计算模型，可以通过参数计算出排版区域
• 建立指标函数，计算生成的排版区域和原来文字区域之间的重合程度
• 设定初始参数，最大化衡量指标，最后得到一个全局 / 局部最优解

图像处理

讨论一张图片中的一部分文字，假设我们能够通过 Erode / Dilate 以及二值化操作将文本处理为黑块，记这些点组成的点集为$T$。对点集$T$逐列扫描，记每一列的子点集为$T_i$。引入超参数$\lambda$，对于每一个$T_i$，若

$$
|T_i|<\lambda(\max{T_i}-\min{T_i})
$$

则将$T_i$从$T$中舍去，即

$$
T:=T-T_i
$$

经过处理，我们能够得到一个大致准确的文本位置的点集$T$，为了方便地计算损失函数，我们不妨假设其在纵向是一个凸图形，然后将其表示为形如

$$
T^*=[(y_{0s},y_{0e}),(y_{1s},y_{e}),...,(y_{ns},y_{ne})]
$$

的形式。上述式子的含义是将其描述为列的集合的形式，而每列又可以表示为列的横坐标和开始和结束的纵坐标的形式（因为我们假设他是凸图形），如果文字是横排的，那只需要假设在横向是凸图形，然后可以得到一个类似的式子，这里就不作展开了。

注意：

• 如果一列没有任何像素，那这一列的表达记作$(\text{y-max},0)$。之所以这么做是因为方便进行比较。

排版计算函数

有非常多的决定排版位置的因素，这里我们选取几个重要的、可推广的因素：

• 起始横坐标 (文本最右侧的横坐标) $x$
• 起始纵坐标 (文本最右侧的纵坐标) $y$
• 文本换行位置 (这个我们将重点讨论)
• 字体大小，在这里我们取每个全角字符占的像素个数 $l_f$
• 文本间距，这里我们取两列字间的空隙像素个数 $d$

接下来我将先讨论文本换行位置，换行位置可以有多种表达形式：

• 一个多维向量，描述每列多少个字 / 多长
• 一个多维向量，描述每个剖分所在的位置
• 一个 One-Hot 编码的多维向量，记录每个字间是被分割

首先，这三种表达都是不可微不可导的，也就带来了一个问题，我们不能用梯度下降来更新这些参数。第二，看第一种表达，他还有一个约束限制，那就是向量的所有维度的值的和必须为文本长度，记作$\sum_i{w_i}=l_t$，增加了处理难度。

然而，我们可以发现，换行情况是可以在有限时间内被枚举出来的。

如果每个文字都可以被换行，假设字符总数为$m$，那么就有$2^{m-1}$中字符情况，这无疑是灾难性的，毕竟这已经是指数复杂度了。

所以，我们需要增加一定的约束条件：

• 列的数量 $k$
• 列的最长字符数量 $m$

基于上面两个约束条件，我们可以给出所有可能的情况枚举，记为$C$。

注意：由于文本有时还会根据需要进行换行（例如停顿、语义的分割），所以跟多的时候，$\vec{c}$可能由用户给出，或者用户给出部分剖分结果。

接下来，我们正对每个字符串分割情况进行讨论，字符串分割记作$\vec{c}$，这里的编码使用上面的第二种编码，记录剖分所在位置，$[c_{i-1},c_i)$就代表第$i$个剖分的区间（采用左闭右开）。

总结一下，我们现在可以用$x,y,l_f,d,\vec{c}$来建立排版函数，除$\vec{c}$外都是需要优化的参数，所以记：

$$
\vec\theta=(x,y,l_f,d)
$$

为参数。

设排版面积函数为：

$$
A(\vec\theta,\vec{c})
$$

这个函数的结果与$\vec{c}$的维度相同，记录每行的横坐标和纵坐标的起始结束位置：

$$
A(\vec\theta,\vec{c})_i=(x-i\times{(l_f+d)},y,y+\sum_{a=c_{i-1}}^{c_i-1}f(t(a)))
$$

注意：

• 上面我们引入了$f(t)$和$t(a)$，分别用来表示字符$t$的像素大小函数和位置$a$的字符$t$。之所以这么做，是因为我们会遇到符号、空格等并非全角的情况。
• 对于某些字符子串，如：西文、连续符号、特殊符号等（都是字符长度超过$1$但是最终渲染长度是$1$ 的情况），会进行预处理，并在计算时被替换成UTF-8占位符，例如：\u0000, \u0001 等。

例子：

将$A$扩展到整个图像大小长度的矩阵$A^*$来得到与$T^*$类似的结果：

$\forall{i\in[0,|\vec{c}|)},\forall{j\in{[0,l_f)}},k=x-i\times{(l_f+d)}$时

$$
A^*(\vec\theta,\vec{c})_{k-j}=(y,y+\sum_{a=c_{i-1}}^{c_i-1}f(t(a)))
$$

其他情况下：

$$
A^*(\vec\theta,\vec{c})_p=(0,0)
$$

计算重合度指标

为了定义原区域$T^*$和计算排版区域$A^*$间的重合程度，定义重合度指标：

$$
L(\vec\theta,\vec{c})=\displaystyle\frac{A^*\cap{T^*}}{A^*\cup{T^*}}=\sum_i\frac{A_i^*\cap{T_i^*}}{A_i^*\cup{T_i^*}}
$$

现在定义$(a,b),(c,d)$间的$\cap,\cup$运算：当$d-a>0,b-c>0$同时成立时（且$(a,b),(c,d)$都是合法区间，初始化时的$(\text{y-max},0)$就是非法区间）：

$$
(a,b)\cap(c,d)=\min(d-a,b-c)
$$

$$
(a,b)\cup(c,d)=\max(d-a,b-c)=(b-a)+(d-c)+(a,b)\cap(c,d)
$$

若条件不成立，则：

$$
(a,b)\cap(c,d)=0
$$

$$
(a,b)\cup(c,d)=(b-a)+(d-c)
$$

总结一下，我们就是计算两个区域交和并的比来计算重合程度，我们希望这个值$L$尽可能逼近$1$

最大化重合度指标

由于$L$满足$0\leq{L}\leq1$，所以我们可以通过梯度上升来达成我们的目标：

$$
\vec\theta:=\vec\theta+\alpha\frac{\partial{L(\vec\theta,\vec{c})}}{\partial{\vec\theta}}
$$

其中，超参数$\alpha$为学习率。

关于是否可导的讨论

无法分析。但是仍旧尝试用梯度上升来优化。我们没办法使用自动求导框架，因为这个过程不支持反向传播。

参考资料和启发

• L1正则和max函数的可导性？: https://www.zhihu.com/question/275630890
• CS231n笔记|3 损失函数和最优化: https://zhuanlan.zhihu.com/p/41679108
• RCF网络损失函数实现: https://github.com/balajiselvaraj1601/RCF_Pytorch_Updated/blob/master/functions.py
• loss函数没导数怎么办？: https://www.zhihu.com/question/268163416
• 如何判断两条轨迹（或曲线）的相似度？: https://www.zhihu.com/question/27213170

实验

见 oom/notebook.ipynb 。下面是一个例子：

• epoch: 100
• L: 55%
• time: 27.7 s
• alpha: 15

Accuracy:

Result:

结论

估算错误，不能自动求导，参数更新速度慢，效果不理想，接下来准备抛弃以重叠为衡量指标的方法。