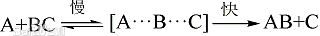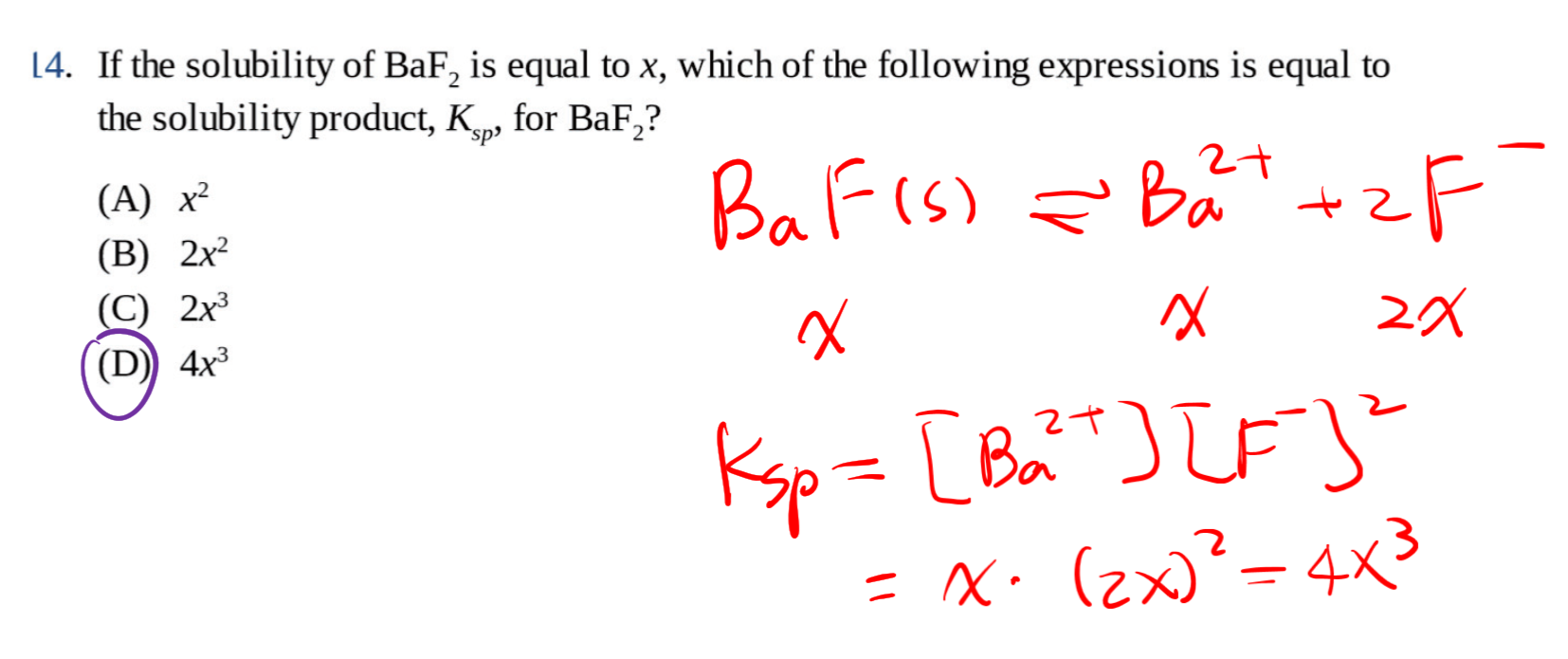- 快死了 - AP Chemistry救急
- 术语 - Terminology
- Reference
- Unit 1 原子结构和性质 - Atomic Structure and Properties
- Unit 2 化合物的结构和性质 - Molecular and Ionic Compound Structure and Properties
- 2.1 化学键 - Chemical Bonds
- 2.1.1 金属键 - Metallic Bonds
- 2.1.2 金属的性质 - Properties of Metals
- 2.1.3 合金 - Alloys
- 2.1.4 离子键 - Ionic Bonds
- 2.1.5 晶格能 - Lattice Energy
- 2.1.6 离子化合物的性质 - Propertied of Ionic Compounds
- 2.1.7 共价键 - Covalent Bonds
- 2.1.8 偶极子 - Dipole
- 2.1.9 偶极矩 - Dipole Moment
- 2.1.10 (非)极性共价键 - (Non)Polar Convalent Bonds
- 2.1.11 分子的极性
- 2.1.12 共价键的形成
- 2.2 路易斯结构图与分子空间构型 - Lewis Structure and Molecular Shape
- 2.3 Hybirdization 杂化
- 2.4 键级、共振、形式电荷 - Bond Order & Resonance & Formal Charge
- 2.1 化学键 - Chemical Bonds
- Unit 3 分子间作用力与性质 - Intermolecular Forces and Properties
- 3.1 分子间作用力 - Intermolecular Forces
- 3.2 固体 - Solid
- 3.3 气体 - Gas
- 3.3.1 理想气体 - Ideal Gas
- 3.3.2 接近理想气体的状态
- 3.3.3 分子动理论 - Kinetic Molecular Theory
- 3.3.4 压缩,温度不变,压强变大,与分子动能无关的解释
- 3.3.5 分子动能和分子运动速率
- 3.3.6 麦克斯韦-玻尔兹曼分布 - Maxwell-Bolzmann Diagram
- 3.3.7 几种压强单位
- 3.3.8 理想气体方程 - Ideal Gas Equation
- 3.3.9 几条气体定律
- 3.3.10 真实气体 - Real Gas
- 3.3.11 分压 - Partial Pressure
- 3.3.12 蒸汽压
- 3.3.13 蒸汽压的影响因素
- 3.4 三态变化
- 3.5 溶液 - Solution
- Unit 4 - Chemical Reaction
- Unit 5 化学动力学 - Chemical Kinetics
- Unit 6 热力学 - Thermodynamics
- 6.1 热力学定律 - Laws of Thermodynamics
- 6.2 化学反应中的能量变化
- 6.3 焓 - Enthalpy
- 6.4 反应焓变的计算
- 9.1 熵与吉布斯自由能 - Entropy & Gibbs Free Energy
- 9.1.0 再论热力学第二定律
- 9.1.1 熵 - Entropy
- 9.1.2 稳定与不稳定
- 9.1.3 熵变 - Change of Entropy
- 9.1.4 判断熵的高低的两条规则
- 9.1.5 吉布斯自由能判断反应是否能自发进行
- 9.1.6 生成吉布斯自由能
- 9.1.7 吉布斯自由能计算方法1 - 通过生成吉布斯自由能
- 9.1.8 吉布斯自由能计算方法2 - $\Delta G = \Delta H - T \Delta S$
- 9.1.9 $\Delta G = \Delta H - T \Delta S$的分析
- 9.1.10 反应由xxx驱动 - Driven By
- 9.1.11 吉布斯自由能计算方法3 - $\Delta G = -RT\ln K$
- 9.1.12 平衡常数$K$与反应是否能自发进行
- 9.1.13 自发发生,但是观察不到产物的原因
- 9.1.14 热化学常数只和温度有关!!!
- 9.1.15 要把热化学常数和动力学的常数区分开!!!
- 9.2 溶解中的能量问题
- Unit 7 化学平衡 - Equilibrium
- Unit 8 酸碱理论 - Acid and Bases
- 8.1 酸碱理论 - Acid and Bases
- 8.2 缓冲溶液 - Buffer Solution
- 8.3 滴定 - Titration
- 8.3.0 标准液的术语
- 8.3.1 中和点/等当量点 - Equivalence Point
- 8.3.2 滴定终点 - Endpoint
- 8.3.3 滴定求浓度
- 8.3.4 滴定判断酸碱的强弱
- 8.3.5 不同酸碱滴定终点的pH比较
- 8.3.6 半等当量点/半中和点 - Half Equivalence Point
- 8.3.7 滴定求$\ce {p K_a}$值
- 8.3.8 滴定图像的分析
- 8.3.9 常用的酸碱指示剂
- 8.3.10 滴定指示剂的选取
- 8.3.11 滴定指示剂的变色范围
- 8.3.12 滴定指示剂的人眼变色范围
- 8.3.13 多元酸的滴定图像 - Polyatomic Acid-Base Titration
- Unit 9 热化学的应用 - Applications of Thermodynamics
- 9.3 电化学 - Electrochemistry
- 9.3.1 原电池 - Voltaic Cell
- 9.3.1.1 原电池 - Voltaic Cell
- 9.3.1.2 原电池阴阳极发生的半反应
- 9.3.1.3 盐桥 - Salt Bridge
- 9.3.1.4 金属活动性顺序
- 9.3.1.5 标准电极电势 $E^\circ$
- 9.3.1.6 反应式中的 $E^\circ$
- 9.3.1.7 $E^\circ$描述电势差
- 9.3.1.8 多个反应式相加$E^\circ$不需要乘系数
- 9.3.1.9 通过$E^\circ$判断原电池反应能否发生
- 9.3.1.10 能斯特方程 - 非标准状态的$E$ - Nernst Equation
- 9.3.1.11 什么是转移的电子数
- 9.3.1.12 非标准状态的$E$的变化的讨论
- 9.3.1.13 $E$与$\Delta G$
- 9.3.1.14 电化学、热力学、与平衡的关系
- 9.3.2 电解池 - Electrolytic Cells
- 9.3.3 电解池与原电池的比较
- 9.3.1 原电池 - Voltaic Cell
- 9.3 电化学 - Electrochemistry
- Appendix - 附录:补充知识
- 零散的小点
快死了 - AP Chemistry救急
术语 - Terminology
| English | 中文 |
|---|---|
| nucleus | 原子核 |
| proton | 质子 |
| neutron | 中子 |
| electron | 电子 |
| ion | 离子 |
| positive ion | 阳离子 |
| negative ion | 阴离子 |
| cation | 阳离子 |
| cationic | 阳离子的 |
| anion | 阴离子 |
| anionic | 阴离子的 |
| alkali metal | 碱金属 |
| alkaline earth metal | 碱土金属 |
| halogen | 卤素 |
| noble gas | 稀有气体 |
| isotope | 同位素 |
| mass number | 质量数 |
| mass spectrum | 质谱图 |
| Florine | $\ce {F2}$ |
| Chlorine | $\ce {Cl2}$ |
| Bromine | $\ce {Br2}$ |
| Iodine | $\ce {I2}$ |
| Oxygen | $\ce {O2}$ |
| Nitrogen | $\ce {N2}$ |
| Hydrogen | $\ce {H2}$ |
| Avogadro | 阿伏伽德罗 |
| Avogadro constant | 阿伏伽德罗常数 |
| glucose | 葡萄糖 |
| Coulomb's Law | 库仑定律 |
| Cathode Ray | 阴极射线 |
| solute | 溶质 |
| solvent | 溶剂 |
| solution | 溶液 |
Reference
- https://baike.baidu.com/item/%E5%81%B6%E6%9E%81%E7%9F%A9/2310034?fr=aladdin
- https://zh.wikipedia.org/wiki/%E7%8E%BB%E5%B0%94%E6%A8%A1%E5%9E%8B
- https://baike.baidu.com/item/%E9%81%93%E5%B0%94%E9%A1%BF%E5%8E%9F%E5%AD%90%E8%AE%BA
- https://baike.baidu.com/item/%E6%B1%A4%E5%A7%86%E5%AD%99%E6%A8%A1%E5%9E%8B/4404079
- http://blog.gaozhongwuli.com/41226
- https://baike.baidu.com/item/%E5%AF%86%E7%AB%8B%E6%A0%B9%E6%B2%B9%E6%BB%B4%E5%AE%9E%E9%AA%8C/9958156https://baike.baidu.com/item/%E6%A0%B8%E5%BC%8F%E5%8E%9F%E5%AD%90%E7%BB%93%E6%9E%84%E6%A8%A1%E5%9E%8B/5716901
- https://baike.baidu.com/item/%E6%A0%B8%E5%BC%8F%E5%8E%9F%E5%AD%90%E7%BB%93%E6%9E%84%E6%A8%A1%E5%9E%8B/5716901
- https://baike.baidu.com/item/%CE%B1%E7%B2%92%E5%AD%90%E6%95%A3%E5%B0%84%E5%AE%9E%E9%AA%8C/819095
- https://baike.baidu.com/item/%E9%87%8F%E5%AD%90%E6%95%B0/2723409
- https://baike.baidu.com/item/%E8%83%BD%E9%87%8F%E6%9C%80%E4%BD%8E%E5%8E%9F%E7%90%86/1442991
- https://baike.baidu.com/item/%E6%B3%A1%E5%88%A9%E4%B8%8D%E7%9B%B8%E5%AE%B9%E5%8E%9F%E7%90%86/773763
- https://baike.baidu.com/item/%E6%B4%AA%E5%BE%B7%E8%A7%84%E5%88%99/9581301
- https://baike.baidu.com/item/%E5%85%89%E7%94%B5%E5%AD%90%E8%83%BD%E8%B0%B1/2540730
- https://baike.baidu.com/item/%E5%90%B8%E6%94%B6%E5%85%89%E8%B0%B1/8250204
- https://periodicity.gyrojeff.top/
- https://periodicity.io/
- https://baike.baidu.com/item/%E5%B1%8F%E8%94%BD%E6%95%88%E5%BA%94/10586133
- https://wenku.baidu.com/view/143495a177232f60dccca148.html
- https://baike.baidu.com/item/%E9%87%91%E5%B1%9E%E9%94%AE/6414358
- https://dict.cnki.net/index#
- https://baike.baidu.com/item/%E7%A6%BB%E5%AD%90%E9%94%AE/549067
- https://baike.baidu.com/item/%E6%99%B6%E6%A0%BC%E8%83%BD/3801806
- https://www.testdaily.cn/34000/
- https://baike.baidu.com/item/%E5%85%B1%E4%BB%B7%E9%94%AE/549226
- https://baike.baidu.com/item/%E5%81%B6%E6%9E%81%E5%AD%90/9821501
- https://baike.baidu.com/item/%E5%81%B6%E6%9E%81%E7%9F%A9/2310034
- https://baike.baidu.com/item/%E8%B7%AF%E6%98%93%E6%96%AF%E7%BB%93%E6%9E%84/9552525
- https://baike.baidu.com/item/%E5%85%AB%E9%9A%85%E4%BD%93%E8%A7%84%E5%88%99/6063592
- https://en.wikipedia.org/wiki/VSEPR_theory
- https://zh.wikipedia.org/wiki/%E4%BB%B7%E5%B1%82%E7%94%B5%E5%AD%90%E5%AF%B9%E4%BA%92%E6%96%A5%E7%90%86%E8%AE%BA
- https://zh.wikipedia.org/wiki/Sp%E6%9D%82%E5%8C%96
- https://wenku.baidu.com/view/89572406710abb68a98271fe910ef12d2bf9a901.html
- https://wenku.baidu.com/view/2e98ade52379168884868762caaedd3382c4b56f.html
- https://baike.baidu.com/item/%E9%94%AE%E7%BA%A7/8797592
- https://baike.baidu.com/item/%E5%85%B1%E6%8C%AF%E7%BB%93%E6%9E%84/5575916
- https://zh.wikipedia.org/wiki/%E5%85%B1%E6%8C%AF_(%E5%8C%96%E5%AD%A6)
- https://baike.baidu.com/item/%E5%BD%A2%E5%BC%8F%E7%94%B5%E8%8D%B7/5759070
- https://baike.baidu.com/item/%E8%BF%87%E6%B8%A1%E6%80%81%E7%90%86%E8%AE%BA/2600181
- https://baike.baidu.com/item/%E9%80%9F%E7%8E%87%E5%B8%B8%E6%95%B0/6971202
- https://baike.baidu.com/item/%E5%9F%BA%E5%85%83%E5%8F%8D%E5%BA%94/2896915
- https://baike.baidu.com/item/%E7%83%AD%E5%8A%9B%E5%AD%A6%E7%AC%AC%E9%9B%B6%E5%AE%9A%E5%BE%8B/924062
- https://baike.baidu.com/item/%E7%83%AD%E5%8A%9B%E5%AD%A6%E7%AC%AC%E4%B8%80%E5%AE%9A%E5%BE%8B/476312
- https://baike.baidu.com/item/%E7%83%AD%E5%8A%9B%E5%AD%A6%E7%AC%AC%E4%BA%8C%E5%AE%9A%E5%BE%8B/473407
- https://baike.baidu.com/item/%E7%83%AD%E5%8A%9B%E5%AD%A6%E7%AC%AC%E4%B8%89%E5%AE%9A%E5%BE%8B/215309
- https://baike.baidu.com/item/%E7%8A%B6%E6%80%81%E5%87%BD%E6%95%B0/2081219
- https://baike.baidu.com/item/%E8%B5%AB%E6%96%AF%E5%AE%9A%E5%BE%8B/4198396
- https://baike.baidu.com/item/%E6%BA%B6%E5%BA%A6%E7%A7%AF/9414610
- https://baike.baidu.com/item/%E5%85%B1%E8%BD%AD%E9%85%B8%E7%A2%B1%E5%AF%B9/6997050
Unit 1 原子结构和性质 - Atomic Structure and Properties
1.1 原子结构与核外电子排布 - Atomic Structure & Electron Configuration
1.1.1 道尔顿原子论 - Dalton's Atomic Theory
- 物质是由微观粒子构成的,叫做原子
- 原子不可再分(错误)
1.1.2 汤姆孙 枣糕模型 - Plum pudding model, J.J.Thomson
由来
探究阴极射线(Cathode Ray)。给阴极射线加一个垂直的电场,发现这是电子束。阴极射线从金属中激发出来,但是原子论说原子不可再分,所以推翻。
内容
除电子外,原子的质量与正电荷如同糕点一样均匀排布,电子则如同枣一样随机嵌入在糕点之中。
1.1.3 密立根油滴实验 - Millikan's Oil-drop experiment
测定电子的带电量,原理不赘述,物理课学过了,就是带点油滴加了个电场与重力相等。
1.1.4 卢瑟福 核式结构 - Rutherford's Model
α 粒子散射实验
- 内容:拿 α 粒子去轰击金箔
- 现象:大部分穿过,部分偏转,少量弹回
- 结论:推翻糟糕模型,提出核式结构
内容:核式结构 / 行星模型
原子的中心有一个很小的核,叫做原子核。原子的全部正电荷质量都集中于此,负电荷的电子在核外空间围绕着原子核高速运转。
1.1.5 玻尔模型
提出原因:
$$
\begin{aligned}
&如果卢瑟福的核式结构正确 \\
&\downarrow \\
&原子中电子绕核高速运动 \\
&\downarrow \\
&加速运动的电子向外辐射电磁波 \\
&\downarrow \\
&原子体系的能量不断变小 \\
&\downarrow \\
&电子的轨道半径越来越小 \\
&\downarrow \\
&绕核电子的旋转频率增加 \\
&\downarrow \\
&放出的辐射是连续的 \\
&\downarrow \\
&光谱的变化应该是连续的 \\
&\downarrow \\
&与实验得到的光谱不一致,矛盾
\end{aligned}
$$
提出:
- 稳定态假设:原子只能处在一系列不连续的能量状态。电子虽然有加速度,但是并不能向外辐射电磁波。原子处于稳定的运动状态(成为定态, ground state)
- 轨道量子假设:原子不同能量状态跟电子的不同轨道运动对应。原子定态不连续,电子轨道分布不连续。
- 跃迁假设:原子从一个定态$E_初$迁跃到另外一个定态$E_末$:
$$E_末 - E_初 = h\nu$$
1.1.6 电子云模型
玻尔模型的局限:只能对氢原子光谱做出解释,不能对有多层电子结构的原子做出解释。后来便有了电子云模型。
1.2 量子力学模型 - Quantum Mechanical Model
1.2.0 电子的运动状态
电子的运动状态由四个量决定:
- 电子层数
- K, L, M, N, O, P, ...
- 电子亚层
- $\ce {1s^2 2s^2 2p^6 3s^2 ...}$
- 电子云的伸展方向
- s电子云,是球形对称的,在核外半径相同处任一方向上电子出现的几率相同
- p电子云,纺锤形,三个伸展方向
- d电子云,五个伸展方向
- ...
- 电子的自旋方向
- 有两个,详见泡利不相容
所以一个原子中每个电子的运动方向都不同
1.2.1 量子数 - Quantum Number (不考)
描述电子的运动状态有四个重要参数:
- 主量子数 ($n$): 1, 2, 3, 4, ... 电子层数
- 角量子数 ($l$): 0, 1, 2, 3, ... 对应 s, p, d, f, ...
- 磁量子数 ($m$): 电子云的伸展方向
- 自旋量子数 ($m_s$): 电子的自旋方向, $\pm \frac 1 2$
1.2.2 电子排布 - Electron Configuration
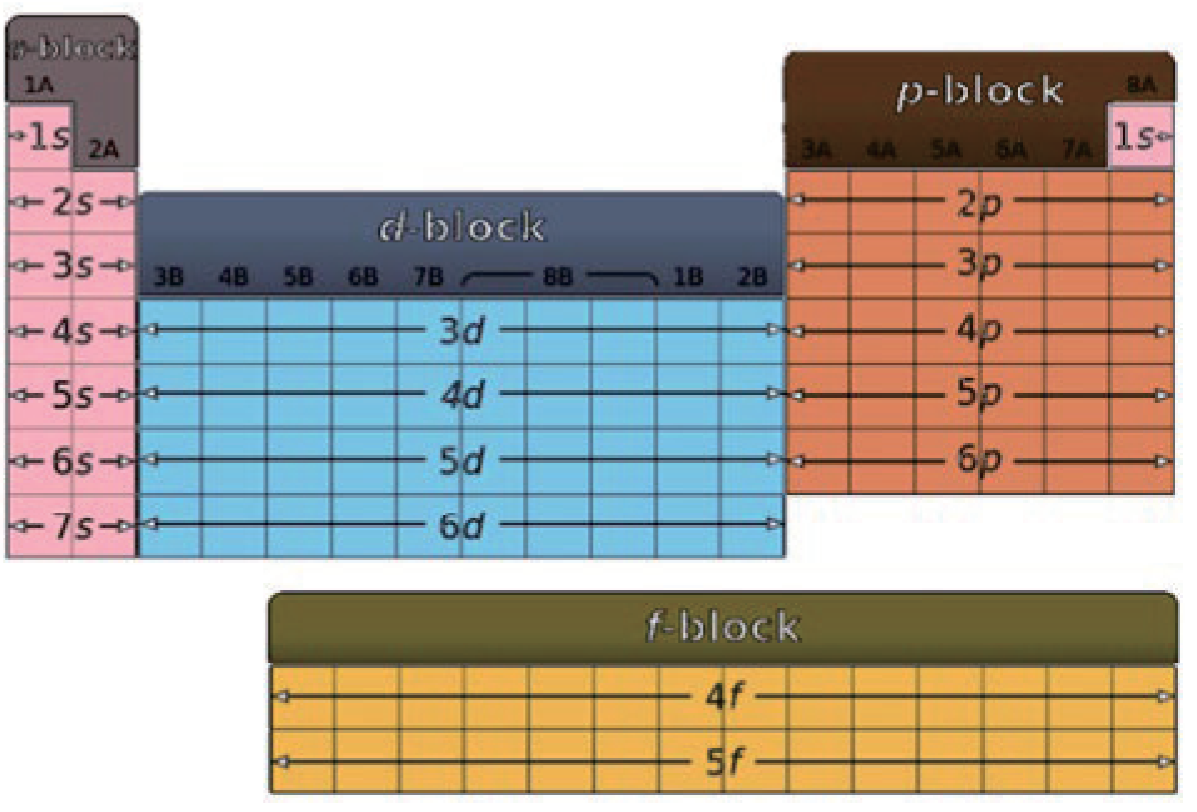
1.2.2.1 能量最低原理 - Lowest Energy Principle / Aufbau Principle
先排满能量低的轨道,再排能量高的轨道。
也由此有能级交错的问题,一张感觉好背的图:
1.2.2.2 泡利不相容原理 - Pauli Exclusion Principle
在原子中完全确定一个电子的状态需要四个量子数,所以泡利不相容原理在原子中就表现为:不能有两个或两个以上的电子具有完全相同的四个量子数,或者说在轨道量子数m,l,n确定的一个原子轨道上最多可容纳两个电子,而这两个电子的自旋方向必须相反。这成为电子在核外排布形成周期性从而解释元素周期表的准则之一。
1.2.2.3 洪德规则 - Hund's Rules
洪特根据大量的光谱实验指出:电子在能量相同的轨道(即等价轨道 )上排布时 ,总是尽可能分占不同的轨道且自旋方向同向,因为这样的排布方式总能量最低,称为洪特规则(Hund’s rule)。
1.2.2.4 离子的电子排布 - Electron Configuration for Ions
- 阳离子:先拿走最外面的而不是能量最高的,举例$4s^2$比$3d^6$先走。
- 阴离子:直接填充就行
1.2.2.5 关于充满和半充满 - Filled & Half-filled
$d^4$和$d^9$的时候会从再外面的轨道拿走一个变成$d^5$和$d^{10}$这样更加稳定
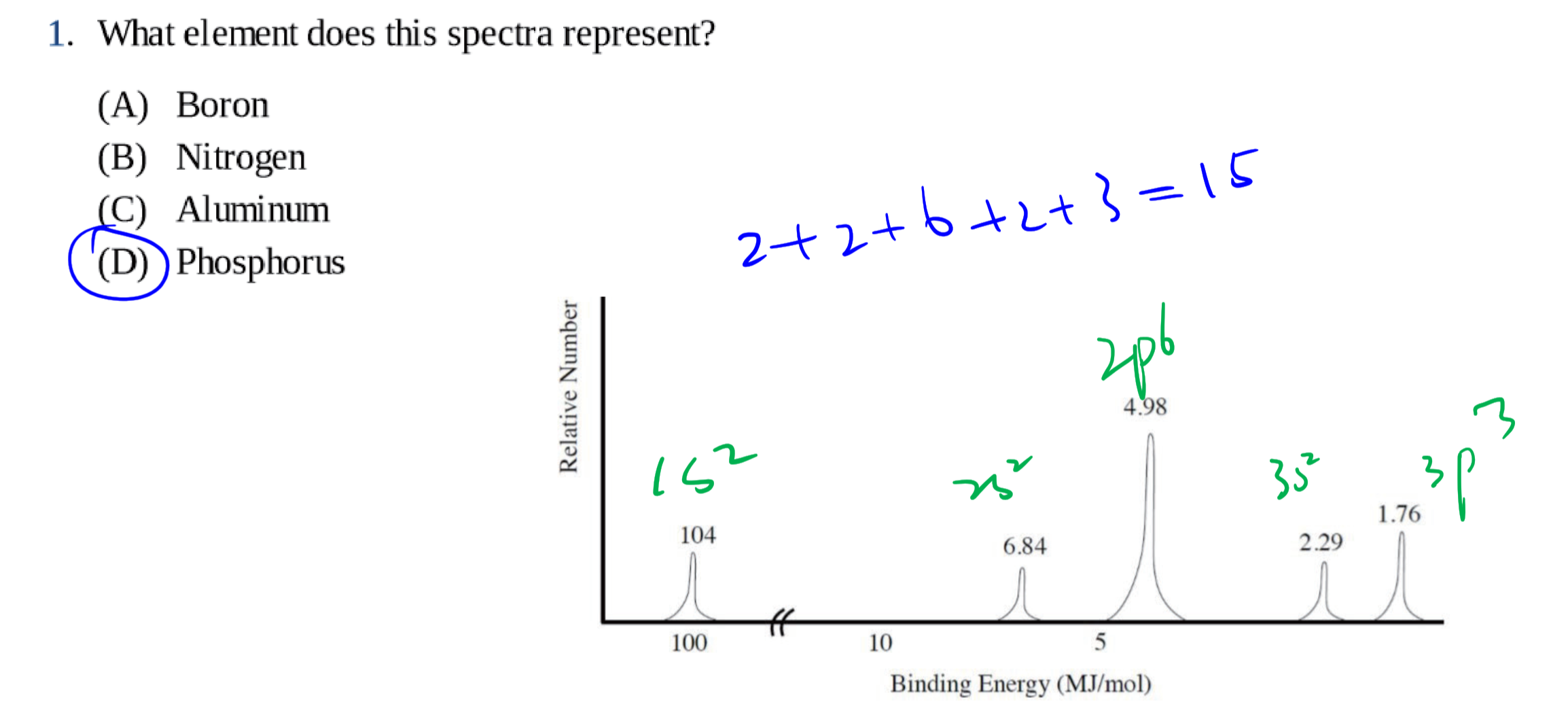
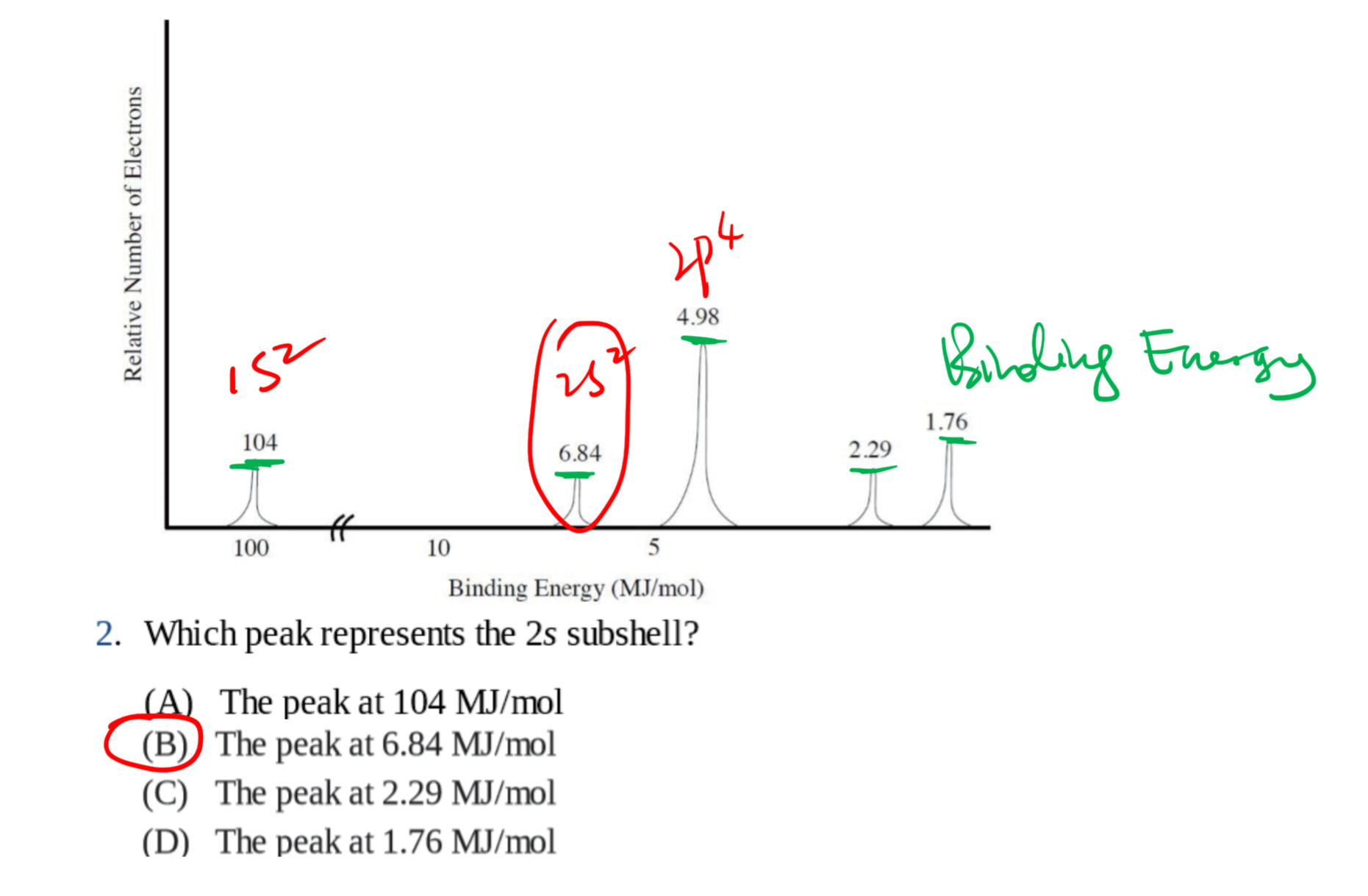
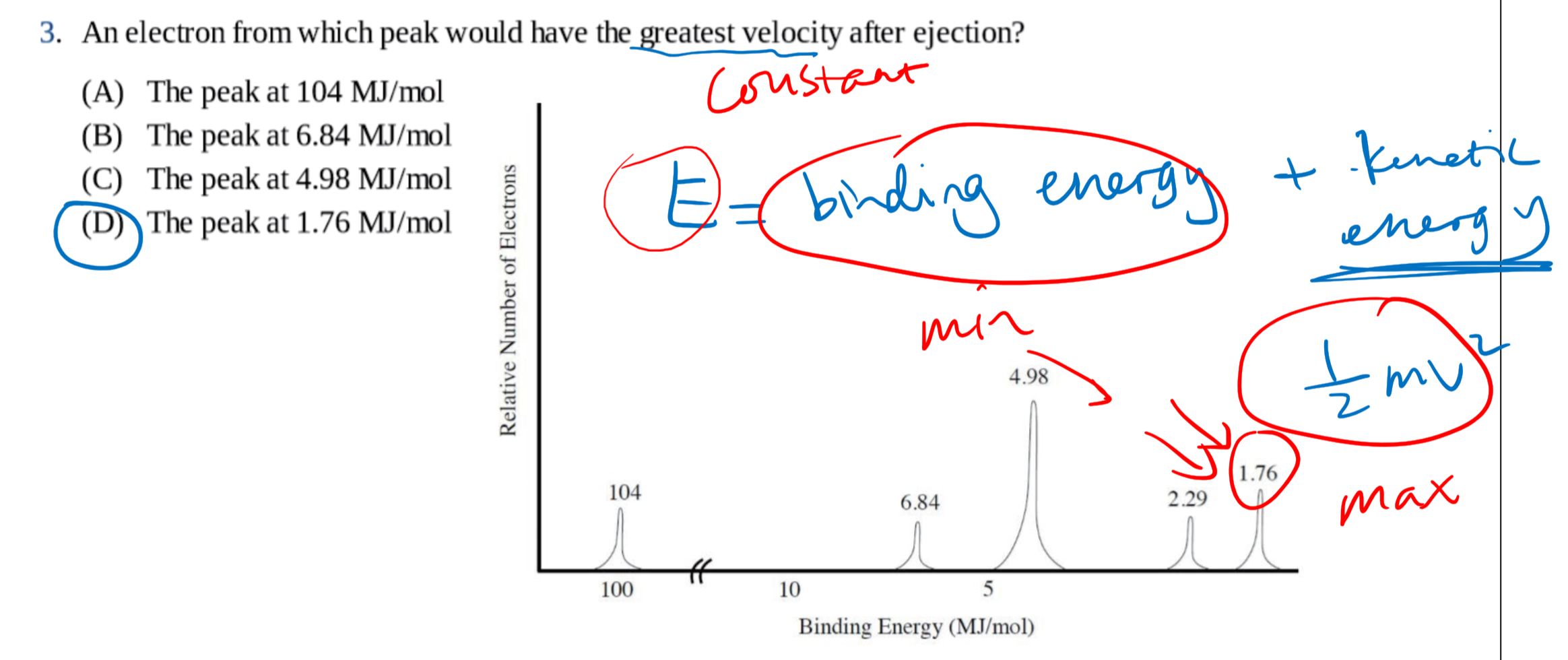
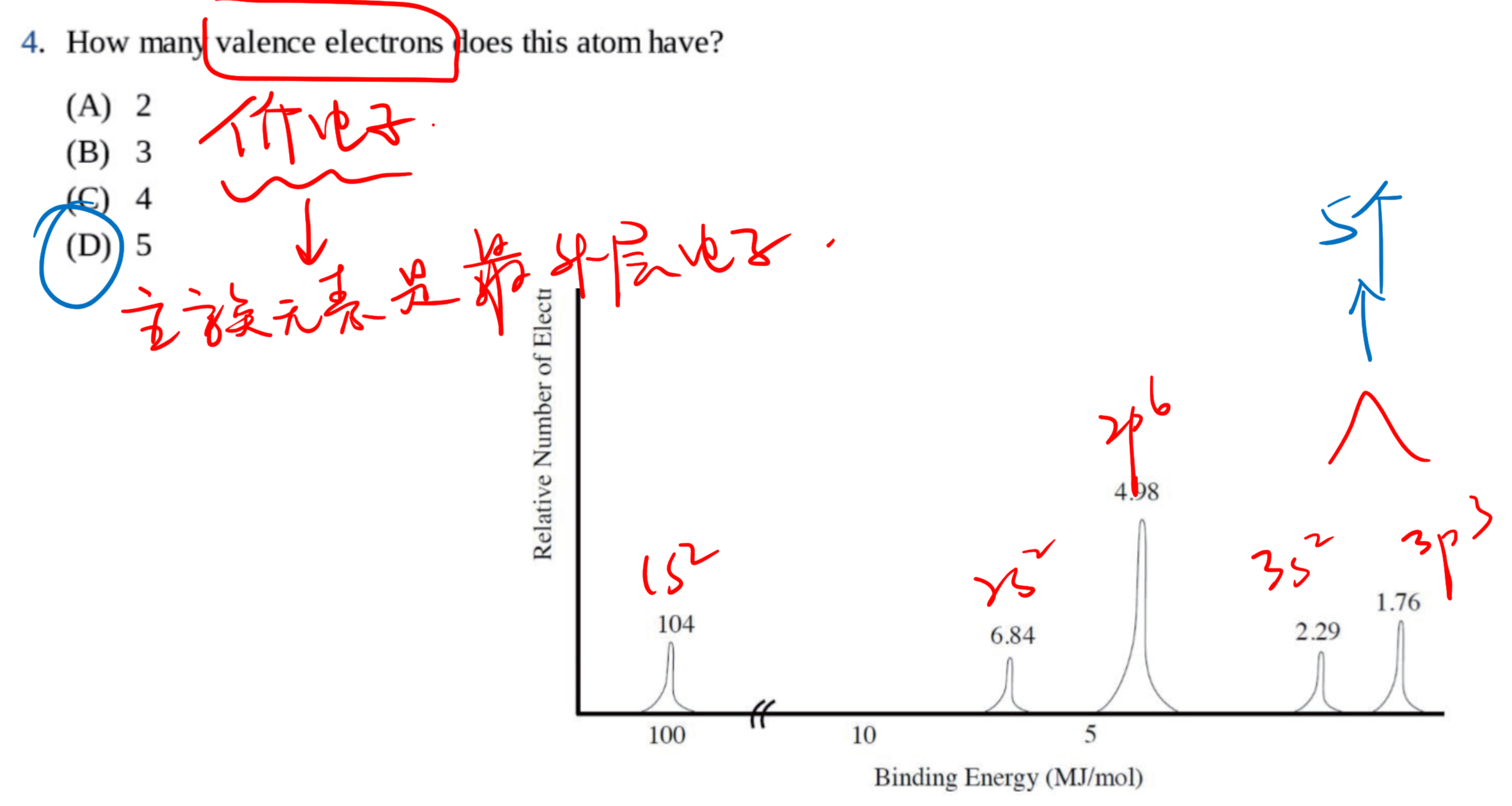
1.3 光电子能谱 - Photoelectron Spectroscopy
光电子能谱(photoelectron spectroscopy),利用光电效应的原理测量单色辐射从样品上打出来的光电子的动能(并由此测定其结合能)、光电子强度和这些电子的角分布,并应用这些信息来研究原子、分子、凝聚相,尤其是固体表面的电子结构的技术。
1.3.1 基本原理
入射的光子能量$h\nu$等于电子克服的结合能$E_B$加上电子获得的动能$E_K$:
$$
\Delta E = h\nu = E_B + E_K = E_B + \frac 1 2 m_e v_e^2
$$
1.3.2 几种常见的考法 / 用法
通过电子个数确定原子:(这里激发的电子个数是看高度)
和电子亚层相关:
和动能相关:
其他:
1.3.3 吸收光谱 - Absorption Spectrum
- Ultraviolet / Visible Radiation (紫外线 / 可见光):Transition in electronic energy levels (电子跃迁)
- 电子排布
- Infrared Radiation (红外线):Molecular Vibrations (分子震动)
- 检测化学键种类
- Microwave Radiation (微波):Molecular Rotations (分子转动)
- 检测分子形状
1.4 周期律 - Periodic Trend
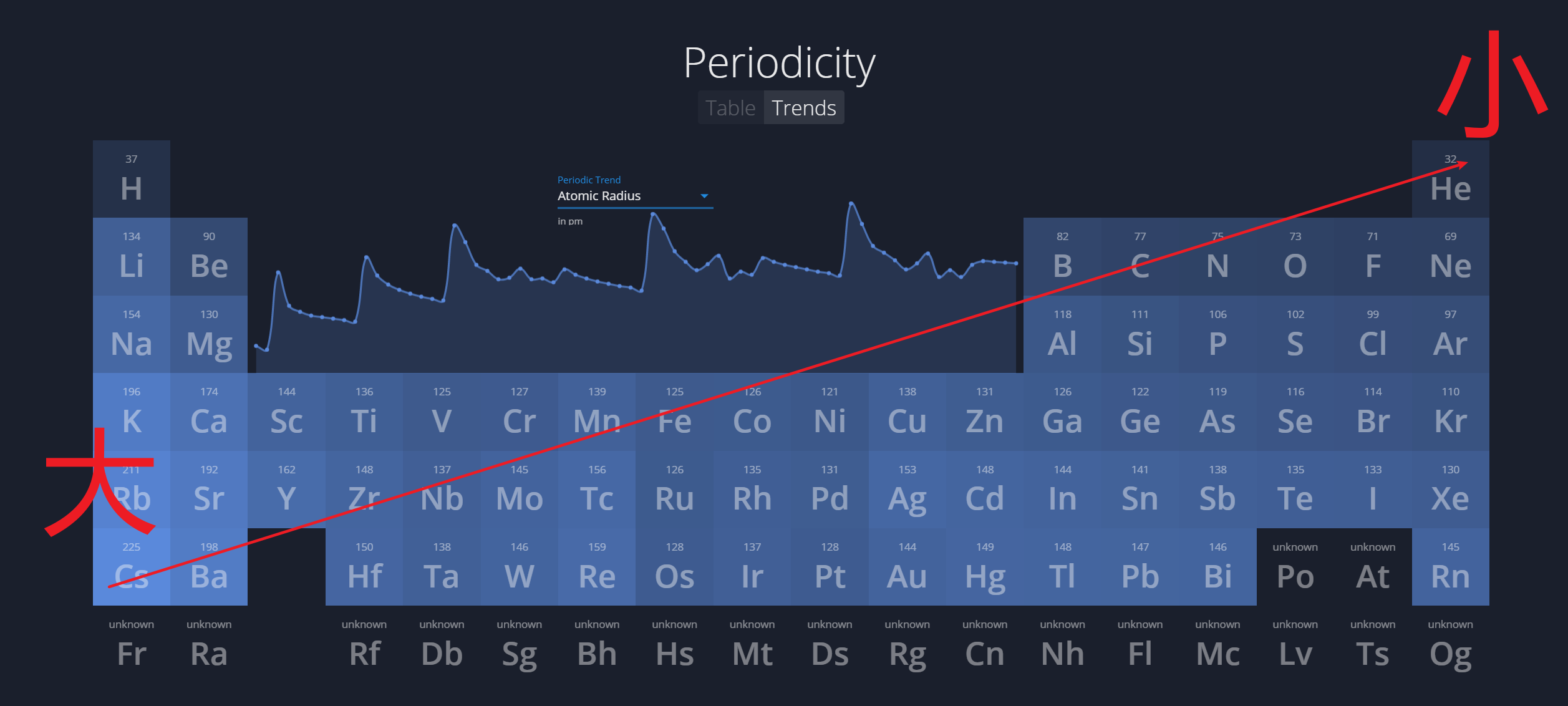
1.4.1 原子半径 - Atomic Radius
原因:
- 从左向右:
$$
\text {attraction between the nuclus and electron} \uparrow
$$ - 从上至下:
$$
\text {additional occupied electron shells}
$$ - 离子比较 ($\ce {r(Cl- ) > r(Cl)}$):
$$
\begin{aligned}
&\begin{cases}
\text {nuclear charge} \leftrightarrow \\
\text {number of electron} \uparrow
\end{cases} \\
\Rightarrow ~&~ \text {repulsion between the electrons} \uparrow
\end{aligned}
$$
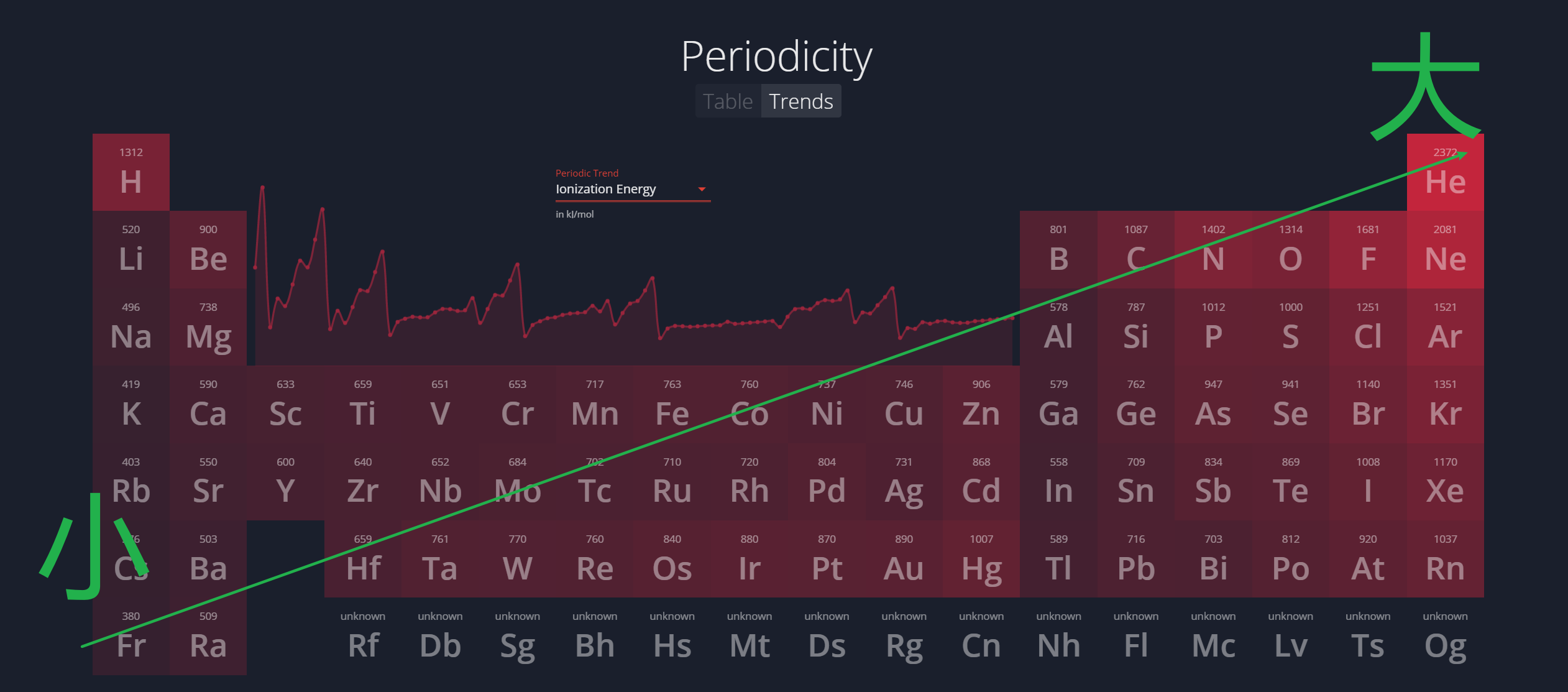
1.4.2 第一电离能 - First Ionization Energy
原因:
- 从左至右:
$$
\begin{aligned}
&\text {nuclear charge} \uparrow \\
\Rightarrow ~&\text {attraction with the outer electron} \uparrow \\
\Rightarrow ~&\text {difficult to remove electron}
\end{aligned}
$$ - 从上至下,除了下面的方法,还可以用 屏蔽效应 (Shielding Effect) 来解释
$$
\begin{aligned}
r \uparrow ~~\Rightarrow F \downarrow
\end{aligned}
$$
1.4.2.1 屏蔽效应 - Shielding Effect
由于其他电子对某一电子的排斥作用而抵消了一部分核电荷对该电子的吸引力,从而引起有效核电荷的降低,削弱了核电荷对该电子的吸引,这种作用称为屏蔽作用或屏蔽效应。
1.4.2.2 有效核电荷 - Effective Nuclear Charge
有效核电荷是指吸引电子的净正电荷。
$$
Z_{\text {eff}} = Z - S
$$
$Z$代表质子数,$S$代表在这个电荷内屏蔽的电荷量 (number of shielding electrons)。
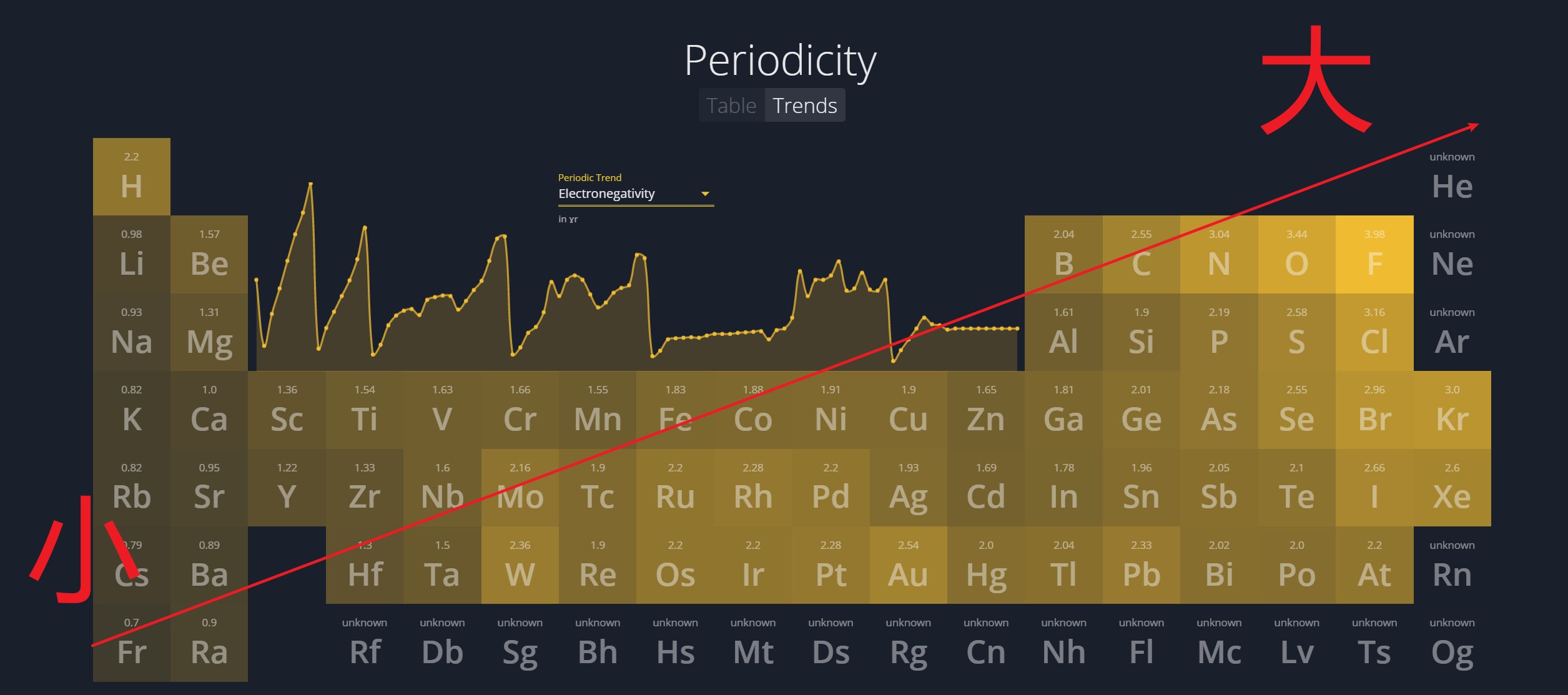
1.4.3 电负性 - Electronegativity
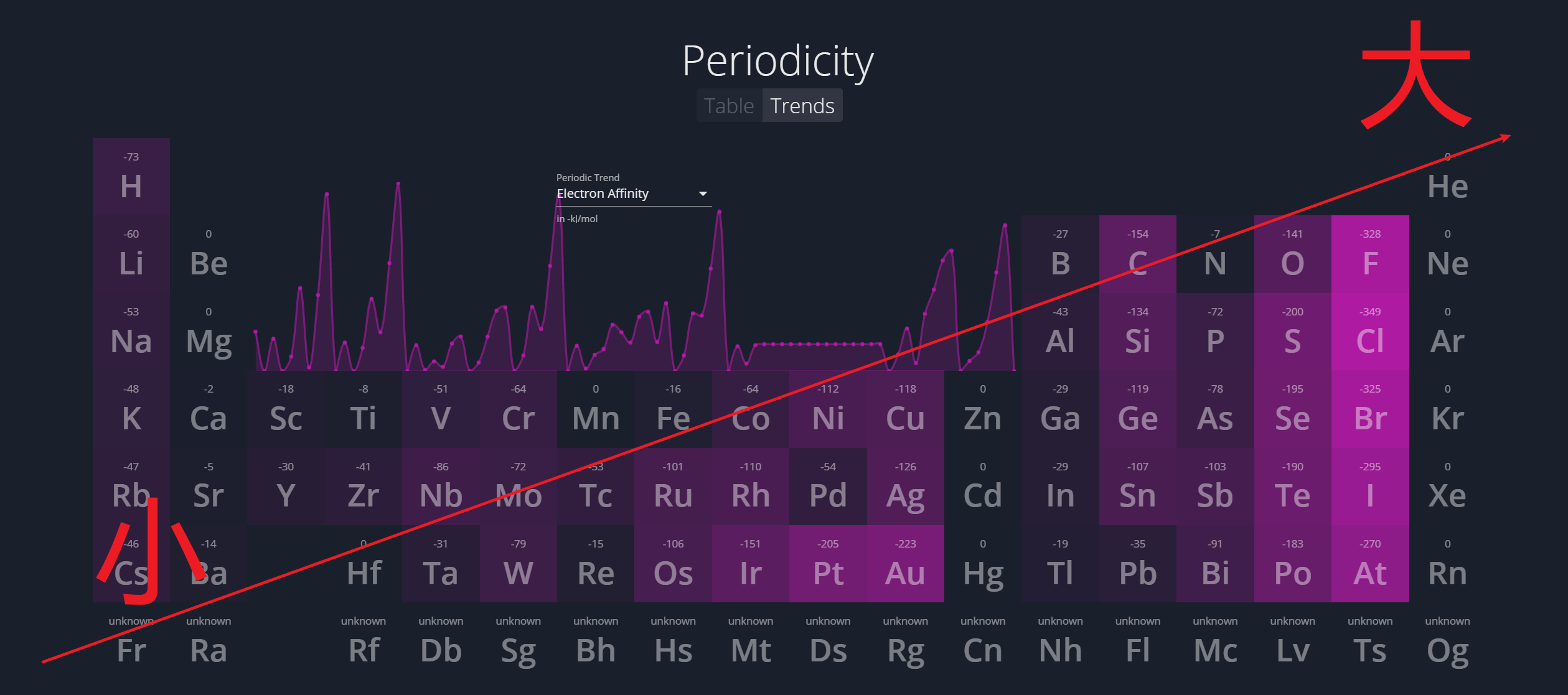
1.4.4 电子亲和能 - Electron Affinity
电子亲和能是基态的气态原子得到电子变为气态阴离子所放出的能量。
Unit 2 化合物的结构和性质 - Molecular and Ionic Compound Structure and Properties
2.1 化学键 - Chemical Bonds
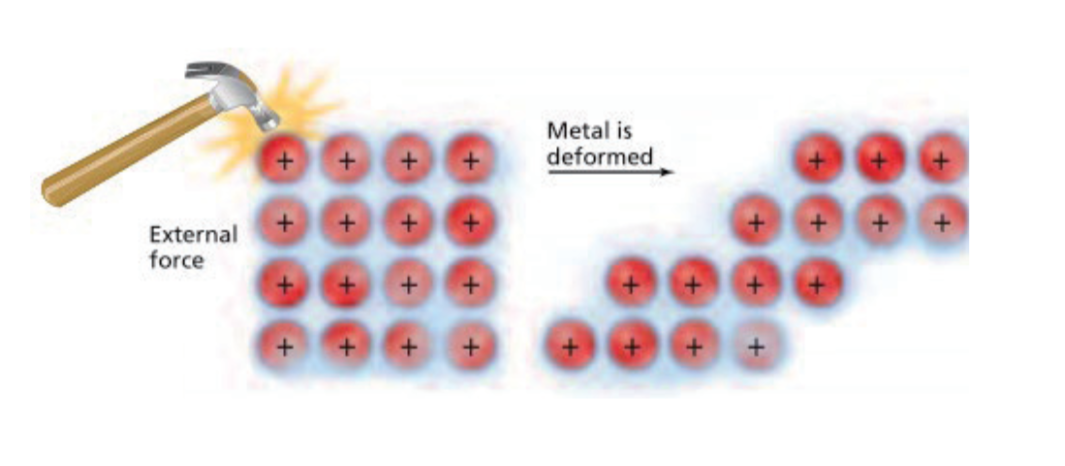
2.1.1 金属键 - Metallic Bonds
- A metallic bond is the attraction of a metallic cation for delocalized electrons. 金属阳离子与自由电子间的强相互作用力。
- 解释了:电、热的良导体
- 熔沸点高低和键能大小之间反向变化
金属晶体中有很多自由电子,在外加电场的作用下可定向移动形成电流,故是电的良导体,在金属一端加热,自由电子热运动加剧,并通过碰撞使未加热处自由电子热运动强度增大,从而将热量传递过去,故也是热的良导体。
2.1.2 金属的性质 - Properties of Metals
- 电、热的良导体
- Malleable and ductile 延展性好 (层与层之间可以互相滑动)
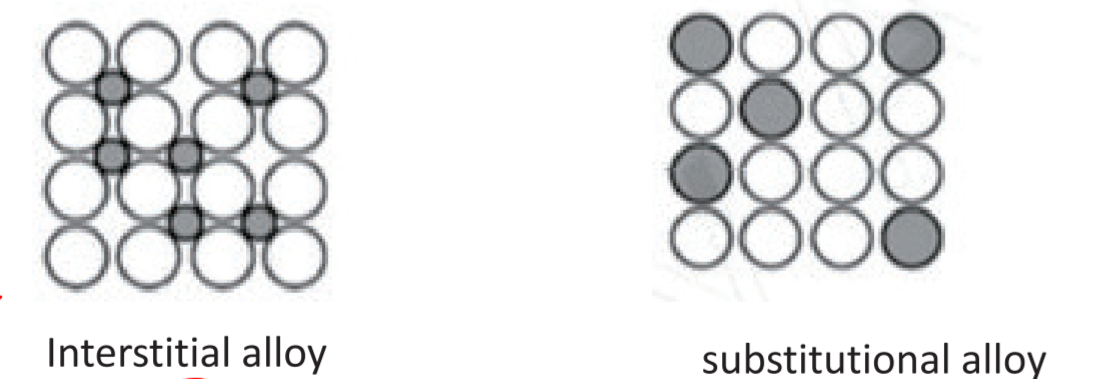
2.1.3 合金 - Alloys
2.1.3.1 填隙式合金 - Interstitial Alloy
原子半径差距很大,填在中间,难以滑动,所以硬
2.1.3.2 置换式合金 - Substitutional Alloy
原子半径相差不大,容易滑动,所以较软
2.1.4 离子键 - Ionic Bonds
离子键的强相互作用力,这种力是静电力 (Electrostatic Force)
常形成于金属阳离子/铵根离子与非金属离子之间。
2.1.5 晶格能 - Lattice Energy
晶格能是指在标准状况下,使离子晶体变成气态正离子和气态负离子时所吸收的能量,它是度量晶格稳定性的参数。
(类似于离子键的键能?)
$$
F \propto \frac {q_1 q_2} {r ^ 2}
$$
重要:比较晶格能的时候,先看带电量,再看半径!!!
2.1.6 离子化合物的性质 - Propertied of Ionic Compounds
一般离子化合物的固体 易碎 (brittle),硬,熔沸点高
2.1.7 共价键 - Covalent Bonds
几个相邻原子通过共用电子并与共用电子之间形成的一种强烈作用叫做共价键。
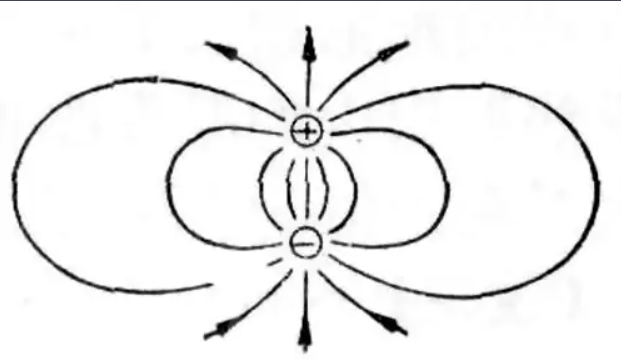
2.1.8 偶极子 - Dipole
偶极子一般指相距很近的符号相反的一对电荷
2.1.9 偶极矩 - Dipole Moment
偶极矩(dipole moment)是正、负电荷中心间的距离和电荷中心所带电量的乘积,它是一个矢量,方向规定为从正电中心指向负电中心,用符号$\mu$表示,单位为D(德拜)。
$$
\mu = \delta \vec d
$$
其中$\delta$表示带的电量。
根据讨论的对象不同,偶极矩可以指键偶极矩,也可以是分子偶极矩。分子偶极矩可由键偶极矩经矢量加法后得到。实验测得的偶极矩可以用来判断分子的空间构型。
2.1.10 (非)极性共价键 - (Non)Polar Convalent Bonds
- 极性共价键:Polar Convalent Bonds
- 非极性共价键:Nonpolar Convalent Bonds
产生原因:
$$
\begin{aligned}
&\text {different atoms} \\
&\downarrow \\
&\text {different electronegativity} \\
&\downarrow \\
&\text {bonding pair is shared unequally} \\
&\downarrow \\
&\text {form dopole}
\end{aligned}
$$
电负性差值越大,电子对偏移程度越大,极性越强
2.1.11 分子的极性
如果$\sum \vec \mu$ 为$\vec 0$,即所有键的偶极矩矢量和为零,则为非极性分子,反之为极性分子。
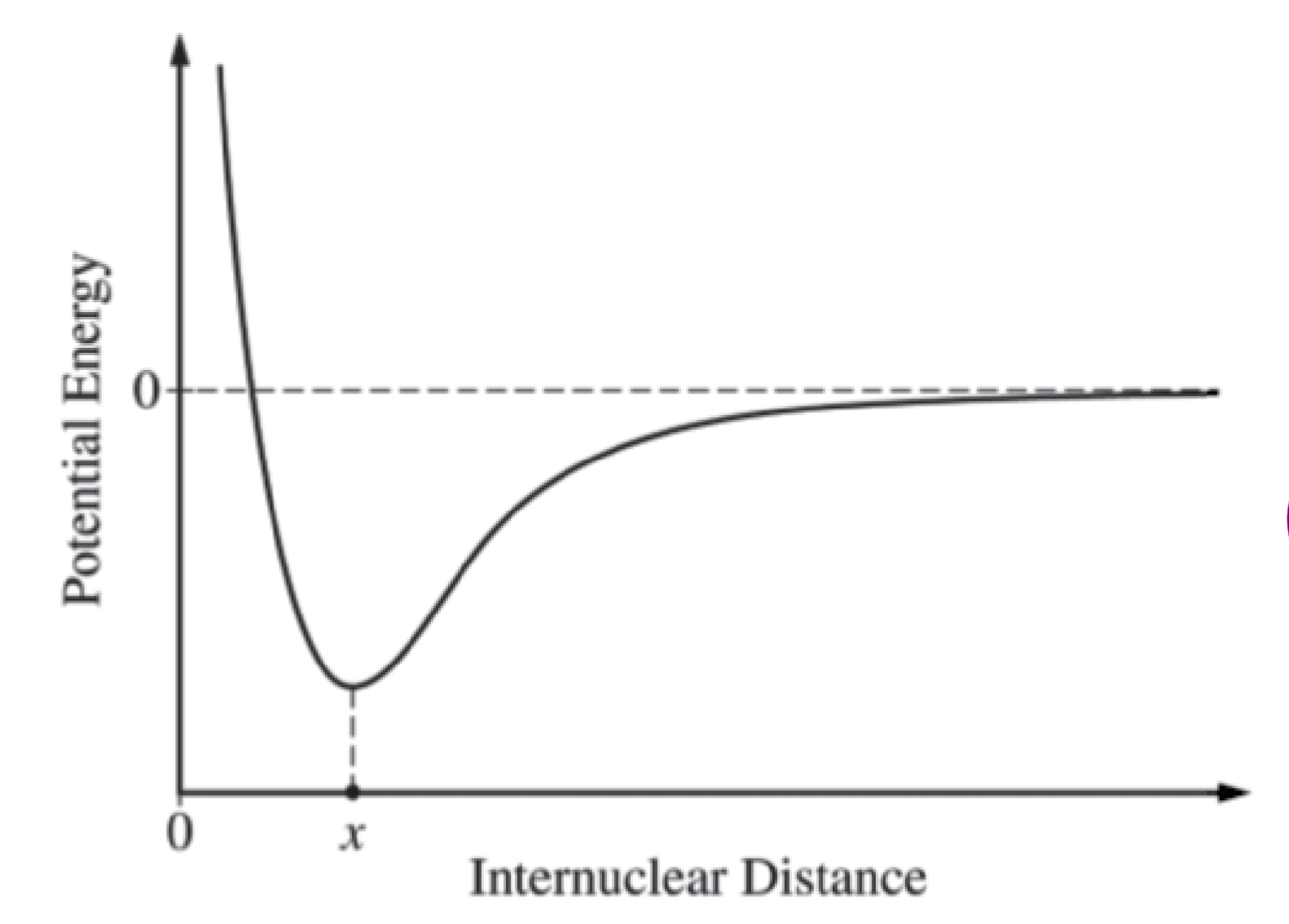
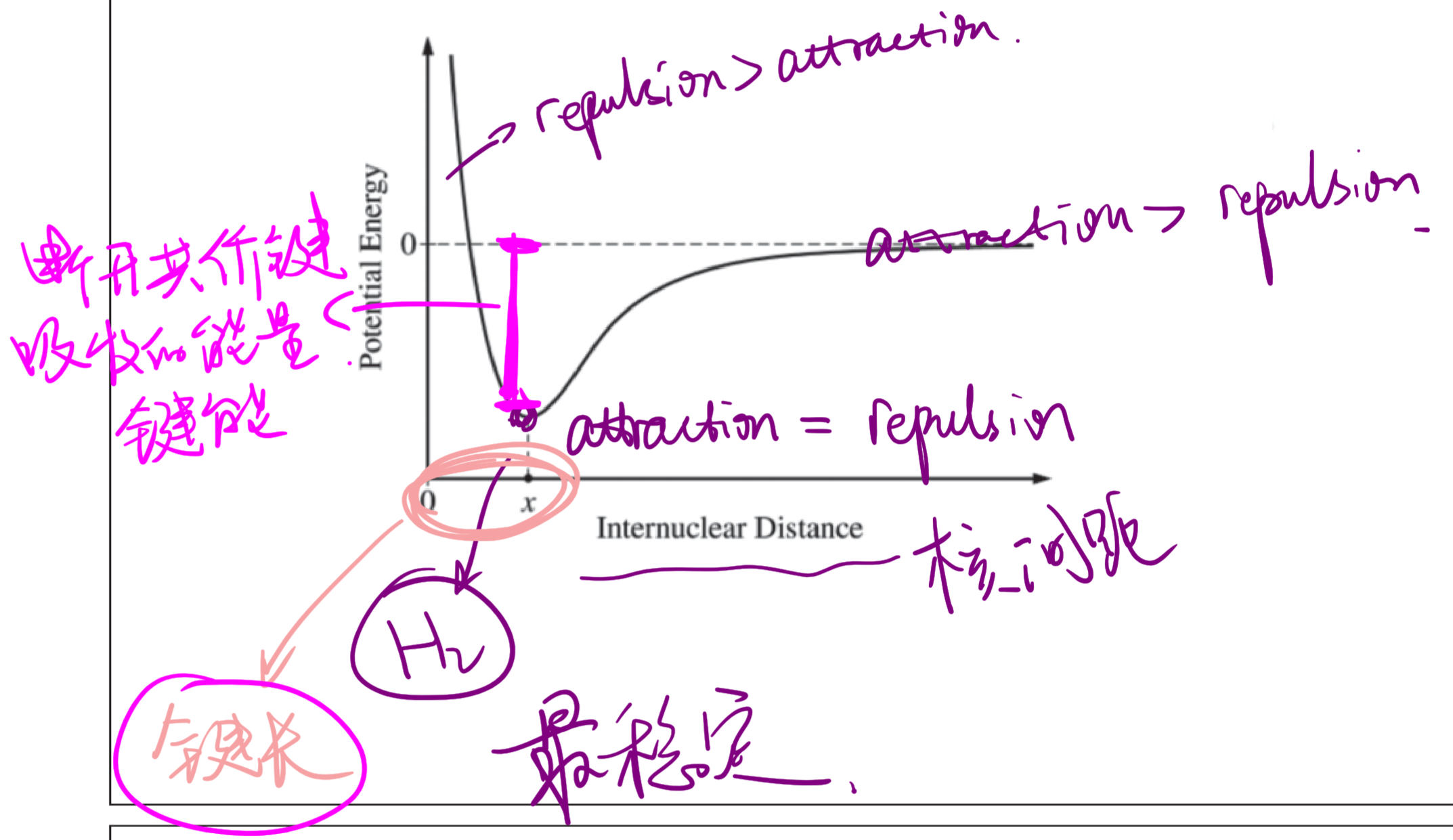
2.1.12 共价键的形成
- 能量越低越稳定,最后键在能量最低处形成,此时的核间距为键长
- 能量最低处到能量为零之间的能量差值是断开共价键所需的能量
2.2 路易斯结构图与分子空间构型 - Lewis Structure and Molecular Shape
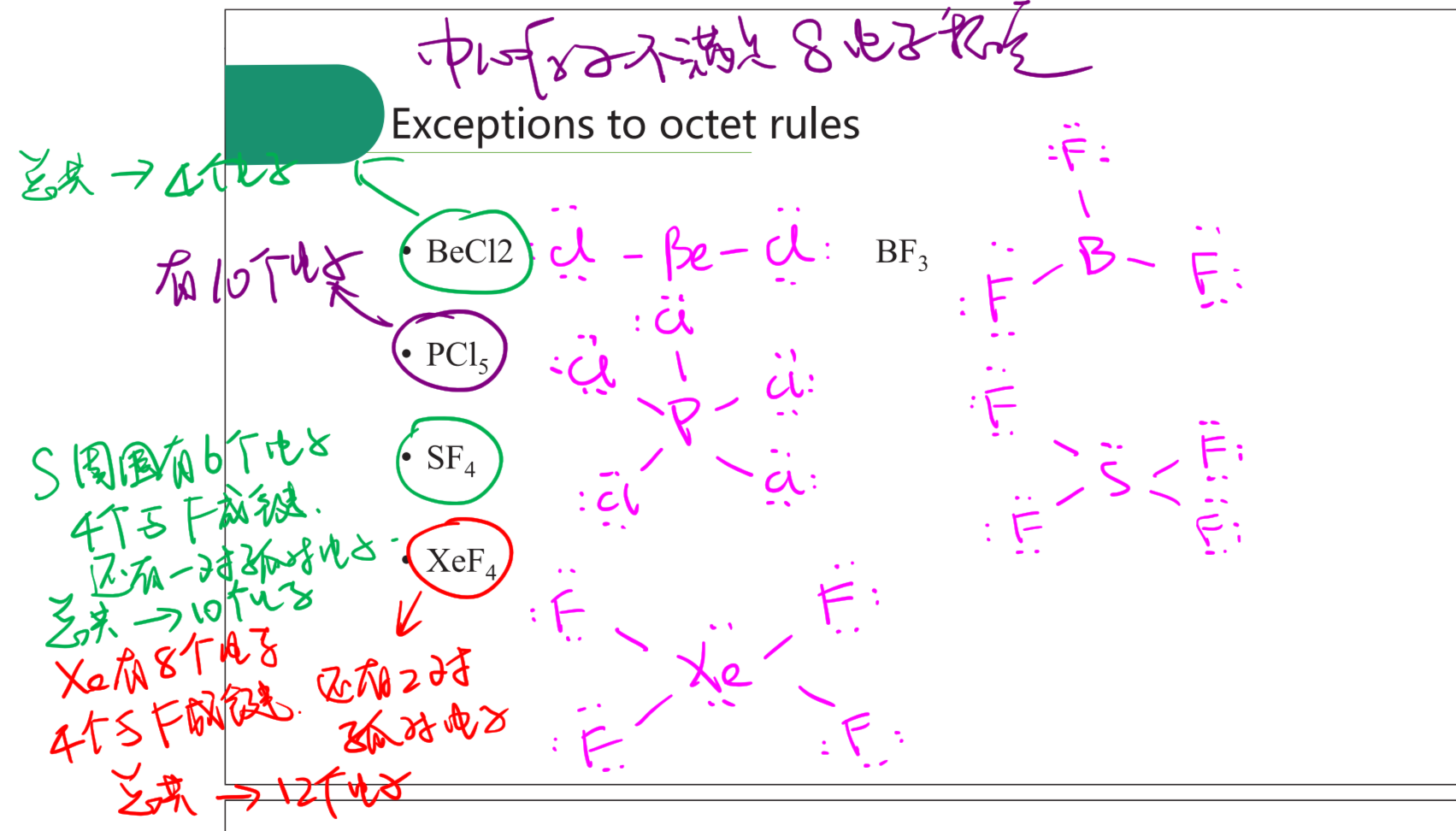
2.2.0 八隅体规则 - Octet Rule
19世纪末,已经有科学家发现配合物是由原子或分子组成,令其组成原子的原子价满足某条件。1893年Alfred Werner发现,与中央连接的原子或官能基的数目(“配位数”)通常是4或者6,最高可以是8,不过罕有发生。1904年,阿贝格提出阿贝格规则,指出元素化合价的最大正值和最小负值的相差通常为8。1916年,Gilbert N. Lewis在其“立方原子理论”制定八隅体规则时就使用了阿贝格规则。
2.2.1 路易斯结构 - Lewis Structure
1916年美国化学家G.N.Lewis提出了共价学说,建立了经典的共价键理论,此理论的核心是原子间通过共用电子对形成最外层8电子的稳定结构(ns2np6)(氢除外)。故路易斯价健理论又称八隅体理论。
A、B 两原子各有一个成单电子,当 A、B 相互接近时,两电子以自旋相反的方式结成电子对,即两个电子所在的原子轨道能相互重叠,则体系能量降低,形成化学键,亦即一对电子则形成一个共价键。
形成的共价键越多,则体系能量越低,形成的分子越稳定。因此,各原子中的未成对电子尽可能多地形成共价键。
配位键形成条件:一种原子中有孤对电子,而另一原子中有可与孤对电子所在轨道相互重叠的空轨道。在配位化合物中,经常见到配位键。
该理论适用于绝大多数主族元素的共价化合物和含共价键的离子,而路易斯结构式的表示要求是:用短线表示原子间形成的共价键,同时用小黑点表示未用于形成共价键的电子(非键合电子),也可省去这些小黑点。这里应注意:非键合电子可以是成对的(孤对电子),也可以是成单的(自由基中)。
2.2.2 路易斯结构图的画法
- Step 1: 确定中心原子(有碳选碳,没碳选电负性小的(大概))
- Step 2: 计算每个原子的价电子数量
- Step 3: 让周围的原子按顺序尽量满足最外层八电子/二电子
- Step 4: 当中心原子已经八电子时,考虑使用配位键让剩下的周围原子满足最外层八点子(下一小结的特例除外)
注:离子的情况比较特殊,有的键看似是配位键,但其实可能并不是,因为除了原子本身的电子之外还有额外提供的电子。
2.2.3 路易斯结构的特例
2.2.4 VSEPR 前置知识
$$
\begin{aligned}
&~~~孤对电子间的排斥力 \\
&>孤对电子与成键电子对间的排斥力 \\
&>成键电子对之间的排斥力
\end{aligned}
$$
2.2.5 VSEPR Model - 价电子互斥模型
Valence Shell Electron Pair Repulsion model:
- A: 中心原子
- X: 成键电子对, 双键 / 三键算一个
- E: 孤对电子
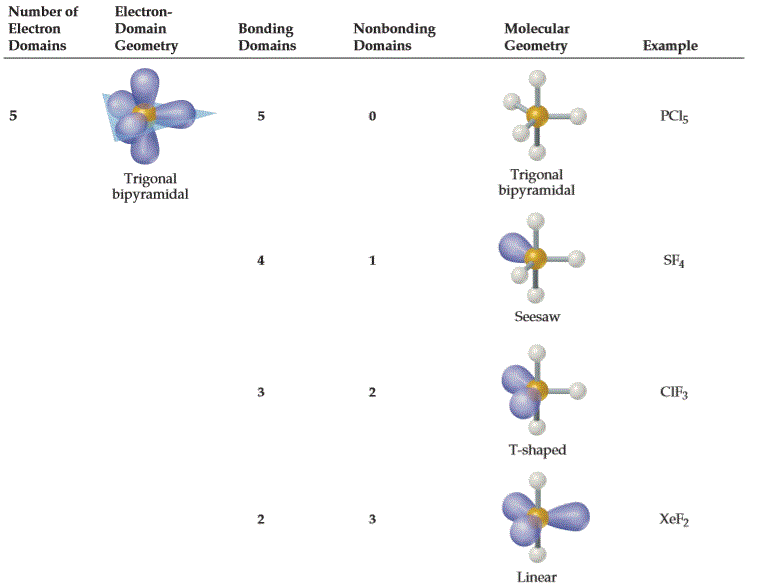
| 分子类型 | 分子形状、角度 | 含中心原子价电子对 | 分子空间结构 | 实例 |
|---|---|---|---|---|
| AX1En | 双原子分子 (直线形) Linear |
HF、O2 | ||
| AX2E0 | 直线形 Linear 180° |
BeCl2、HgCl2、CO2 | ||
| AX3E0 | 平面三角形 Trigonal Planar 120° |

|

|
BF3、CO32−、NO3−、SO3 |
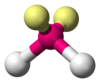
| AX2E1 | 角形 Bent / Angular 119° (< 120°) |

|

|
NO2−、SO2、O3 |
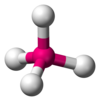
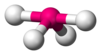
| AX4E0 | 正四面体形 Tetrahedral 109.5° |

|

|
CH4、PO43−、SO42−、ClO4− |
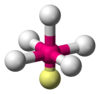
| AX3E1 | 三角锥形 Trigonal Pyramidal 107° (< 109.5°) |

|

|
NH3、PCl3 |
| AX2E2 | 角形 Bent / Angular 104.5° (< 109.5°) |

|

|
H2O、OF2 |
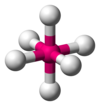
| AX5E0 | 三角双锥形 Trigonal Bipyramidal 90°, 120°, 180° |

|

|
PCl5 |
| AX4E1 | 变形四面体形 (跷跷板形) Seesaw / Disphenoidal 90°, 101.6°, 173.1° |

|

|
SF4 |
| AX3E2 | T字形 T-Shaped 87.5°, < 180° |

|

|
ClF3、BrF3 |
| AX2E3 | 直线形 Linear 180° |

|
XeF2、I3− | |
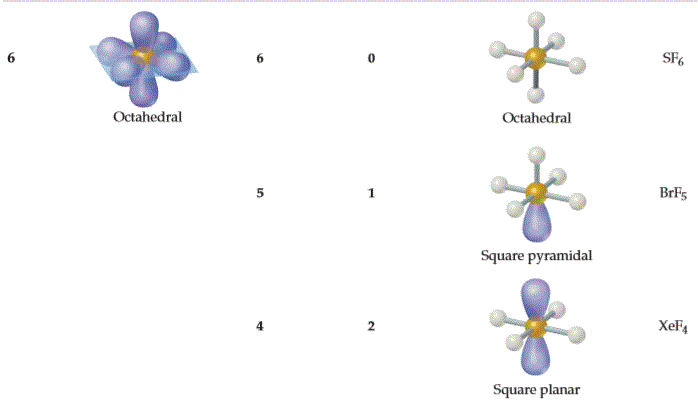
| AX6E0 | 八面体形 Octahedral 90°, 180° |

|

|
SF6 |
| AX5E1 | 四角锥形 Square Pyramidal < 90°, < 180° |

|

|
ClF5、BrF5 |
| AX4E2 | 平面四方形 Square Planar 90°, 180° |

|

|
XeF4 |
2.2.6 再论分子的极性
如下三种情况,分子是非极性的:
- VSEPR模型中,E = 0,且X的几个End atom是相同的
- AX2E3 (Linear), AX4E2 (Square Planar)
- 在AP Chem当中,碳氢化合物 一般 都是非极性的
注意:在解释的时候,需要用之前的 "all the dipoles in the molecule can be cancelled out" 或者 "the vector sum of the dipole moments of all bonds in the molecule is zero" 诸如此类的话。
2.3 Hybirdization 杂化
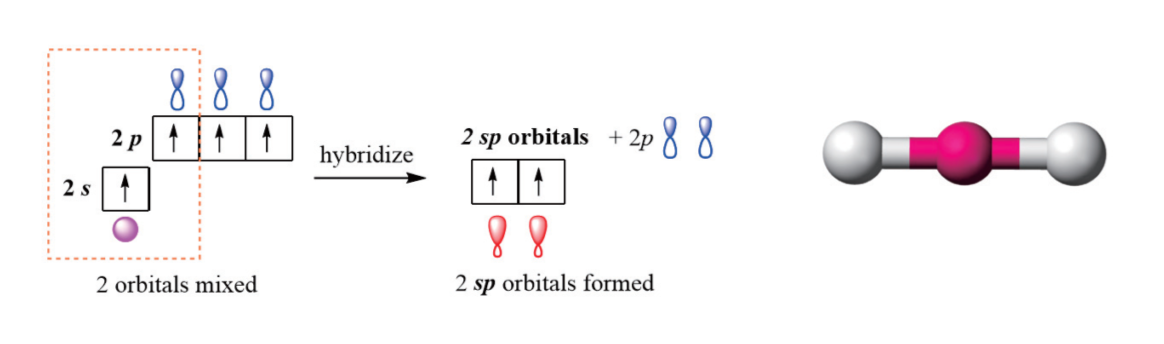
2.3.1 sp杂化 - sp hybridization
sp杂化(英语:sp hybridization)是指一个原子同一电子层内由一个ns轨道和一个np轨道发生杂化的过程。sp杂化是最简单的杂化形式。原子发生sp杂化后,上述ns轨道和一个np轨道便会转化成为两个等价的原子轨道,称为“sp杂化轨道”。两个sp杂化轨道的对称轴夹角为180°,在同一条直线上,故sp杂化也称为“直线型杂化”。[1]sp杂化一般发生在分子形成过程中。杂化发生前,原子最外层s轨道中的一个电子被激发至p轨道,使将要发生杂化的原子进入激发态;之后,该层的s轨道与三个p轨道中的任意一个发生杂化。此过程中,能量相近的s轨道和p轨道发生叠加,不同类型的原子轨道重新分配能量。
以铍原子为例,铍原子在成键时一般采用sp杂化形式:处于基态的铍原子(电子排布式为:1s22s2)的一个2s电子激发至一个空的2p轨道上,成为激发态(电子排布式为:1s22s12p1)。然后,一个2s轨道再和上述填充了一个电子的2p轨道进行sp杂化,形成两个sp杂化轨道。[2]该过程中铍原子的原子轨道排布变化情况如下图所示:
sp杂化对应的轨道空间构型:直线型
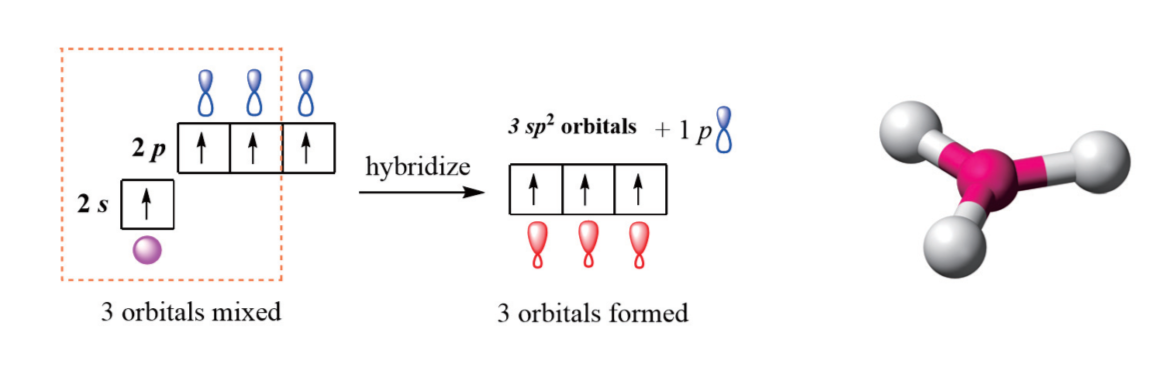
2.3.2 sp2杂化 - sp2 hybirdization
sp2杂化(英语:sp2 hybridization)是指一个原子同一电子层内由一个ns轨道和两个np轨道发生杂化的过程。原子发生sp2杂化后,上述ns轨道和np轨道便会转化成为三个等价的原子轨道,称为“sp2杂化轨道”。三个sp2杂化轨道的对称轴在同一条平面上,两两之间的夹角皆为120°。sp2杂化一般发生在分子形成过程中。杂化发生前,原子最外层s轨道中的一个电子被激发至p轨道,使将要发生杂化的原子进入激发态;之后,该层的s轨道与三个p轨道中的任意两个发生杂化。此过程中,能量相近的s轨道和p轨道发生叠加,不同类型的原子轨道重新分配能量并调整方向。
以硼原子为例,硼原子在成键时一般采用sp2杂化形式:处于基态的硼原子(电子排布式为:1s22s22p1)的一个2s电子激发至一个空的2p轨道上,使原子进入激发态(电子排布式为:1s22s12p2)。然后,一个2s轨道再和上述两个各填充了一个电子的2p轨道进行sp2杂化,形成三个sp2杂化轨道。该过程中硼原子的原子轨道排布变化情况如下图所示:
sp2杂化对应的轨道空间构型:平面三角形 Trigonal Planar
2.3.3 sp3杂化 - sp3 hybirdization
sp3杂化(英语:sp3 hybridization)是指一个原子同一电子层内由一个ns轨道和三个np轨道发生杂化的过程。原子发生sp3杂化后,上述ns轨道和np轨道便会转化成为四个等价的原子轨道,称为“sp3杂化轨道”。四个sp3杂化轨道的对称轴两两之间的夹角相同,皆为109°28'。sp3杂化一般发生在分子形成过程中。杂化发生前,原子最外层s轨道中的一个电子被激发至p轨道,使将要发生杂化的原子进入激发态;之后,该层的s轨道与三个p轨道发生杂化。此过程中,能量相近的s轨道和p轨道发生叠加,不同类型的原子轨道重新分配能量并调整方向。
以碳原子为例:处于基态的碳原子(电子排布式为:1s22s22p2)的一个2s电子激发至一个空的2p轨道上,使原子进入激发态(电子排布式为:1s22s12p3)。然后,一个2s轨道再和上述三个各填充了一个电子的2p轨道进行sp3杂化,形成四个sp3杂化轨道。该过程中碳原子的原子轨道排布变化情况如下图所示:
sp3杂化对应的轨道空间构型:正四面体 Tetrahedral
2.3.4 杂化与VSEPR
注意:杂化轨道中不仅可以有 成键电子对,还可以有 孤对电子
| 电子对数 | 杂化类型(混层类型) | 轨道形状 | 单电子对数(孤电子对) | 分子形状 | 例 |
|---|---|---|---|---|---|
| 2 | sp | 直线形 | 0 | 直线形 | BeCl2、CO2 |
| 3 | sp2 | 平面正三角形 | 0 | 平面正三角形 | BCl3 |
| 1 | V字形(角形、弯曲形) | SO2 | |||
| 4 | sp3 | 正四面体 | 0 | 正四面体 | CH4 |
| 1 | 三角锥 | NH3 | |||
| 2 | V字形(角形、弯曲形) | H2O |
2.4 键级、共振、形式电荷 - Bond Order & Resonance & Formal Charge
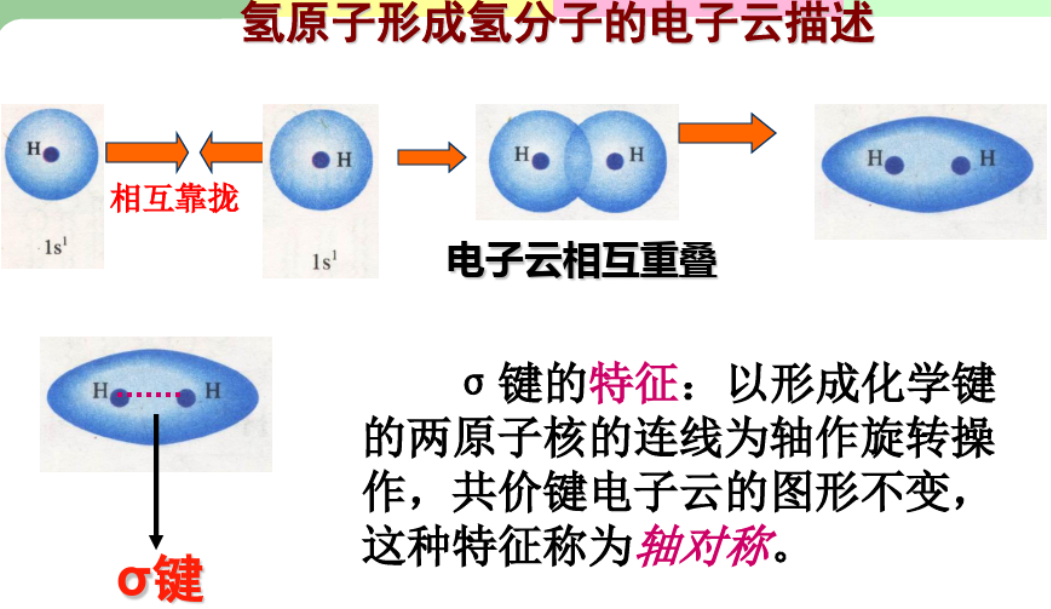
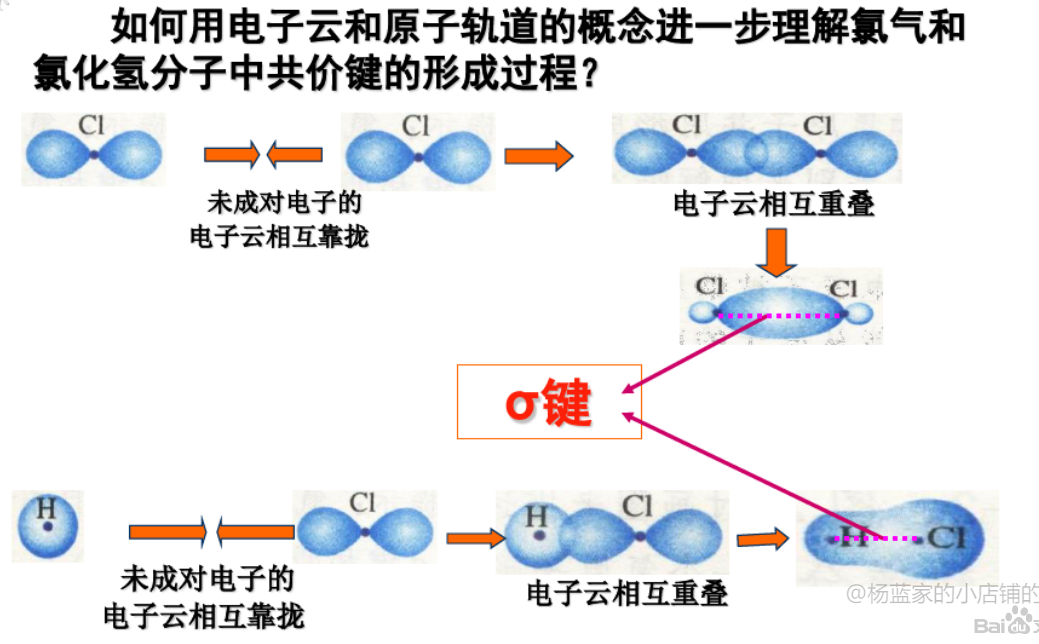
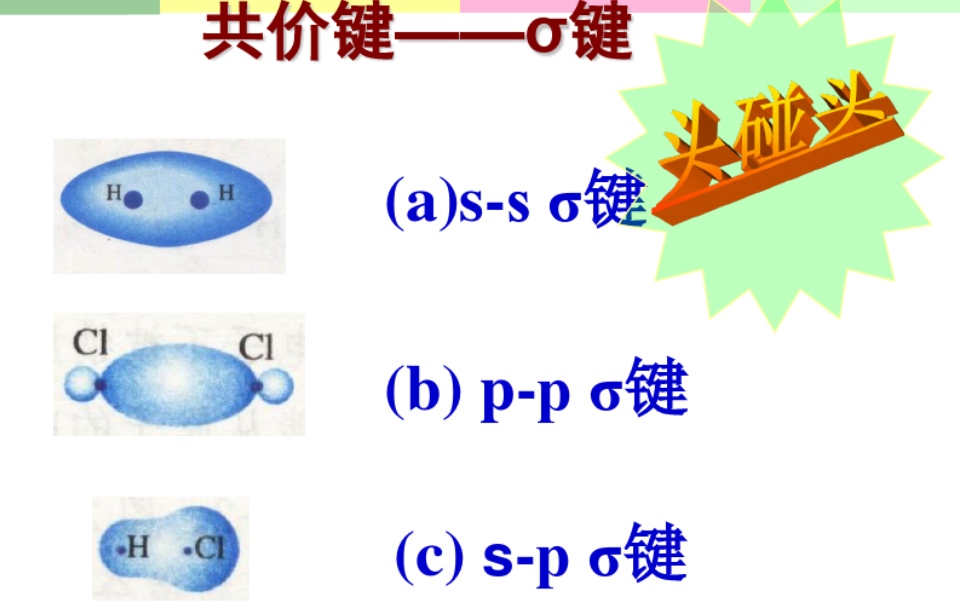
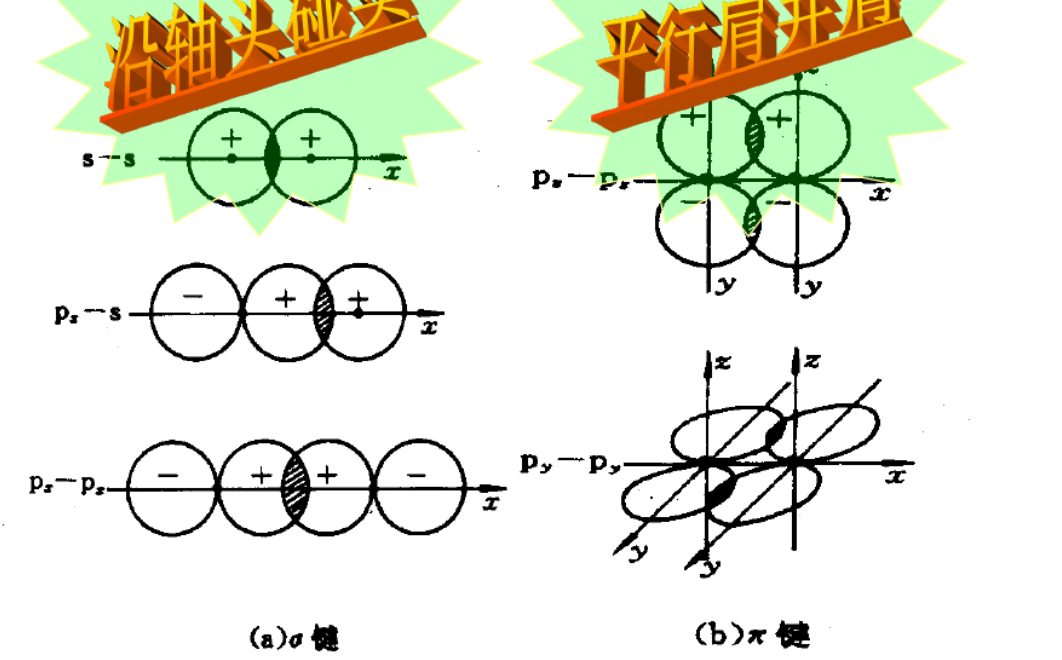
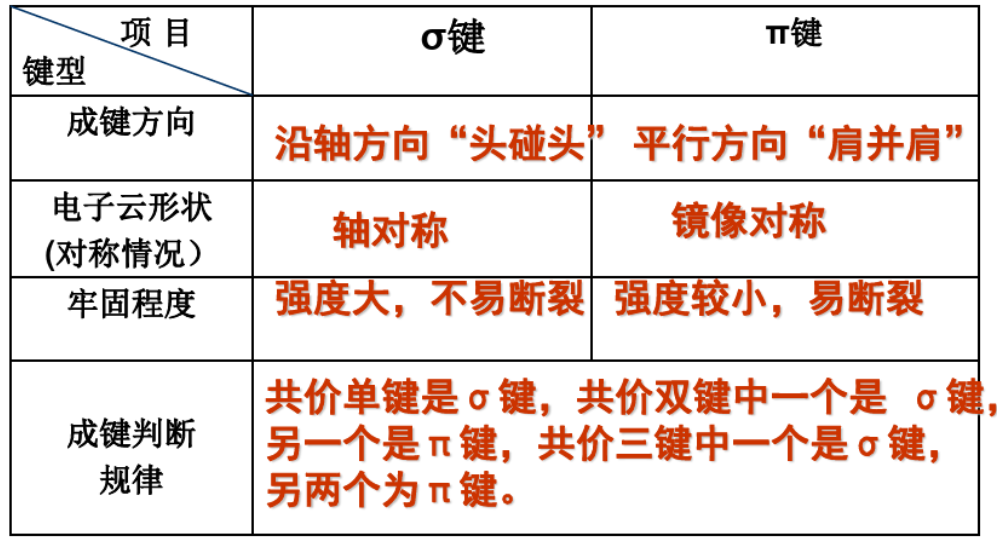
2.4.1 $\sigma$键 - $\sigma$ bond
$\sigma$键是由电子云“头碰头”重叠形成,三种$\sigma$键:
- $s - s ~ \sigma$键
- $p - p ~ \sigma$键
- $s - p ~ \sigma$键
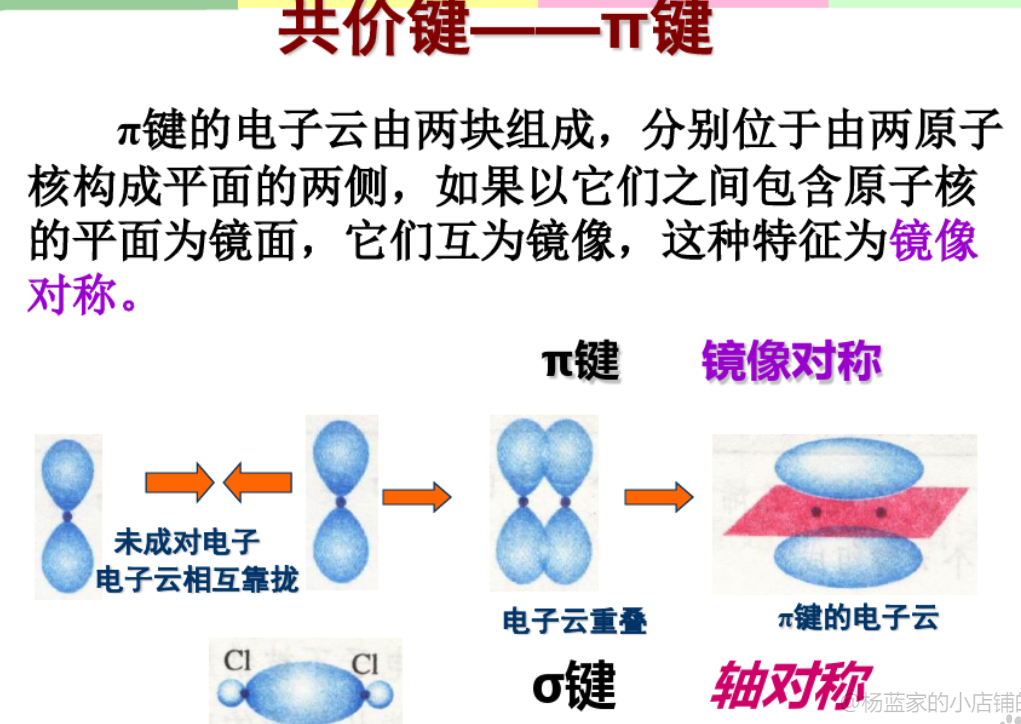
2.4.2 $\pi$键 - $\pi$ bond
由两块电子云组成,比$\sigma$键强度低。
2.4.3 $\sigma$键与$\pi$键比较
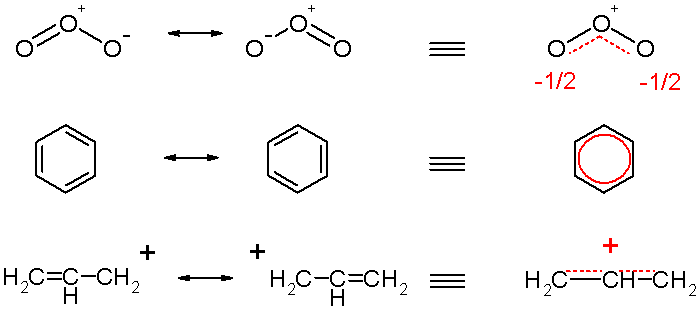
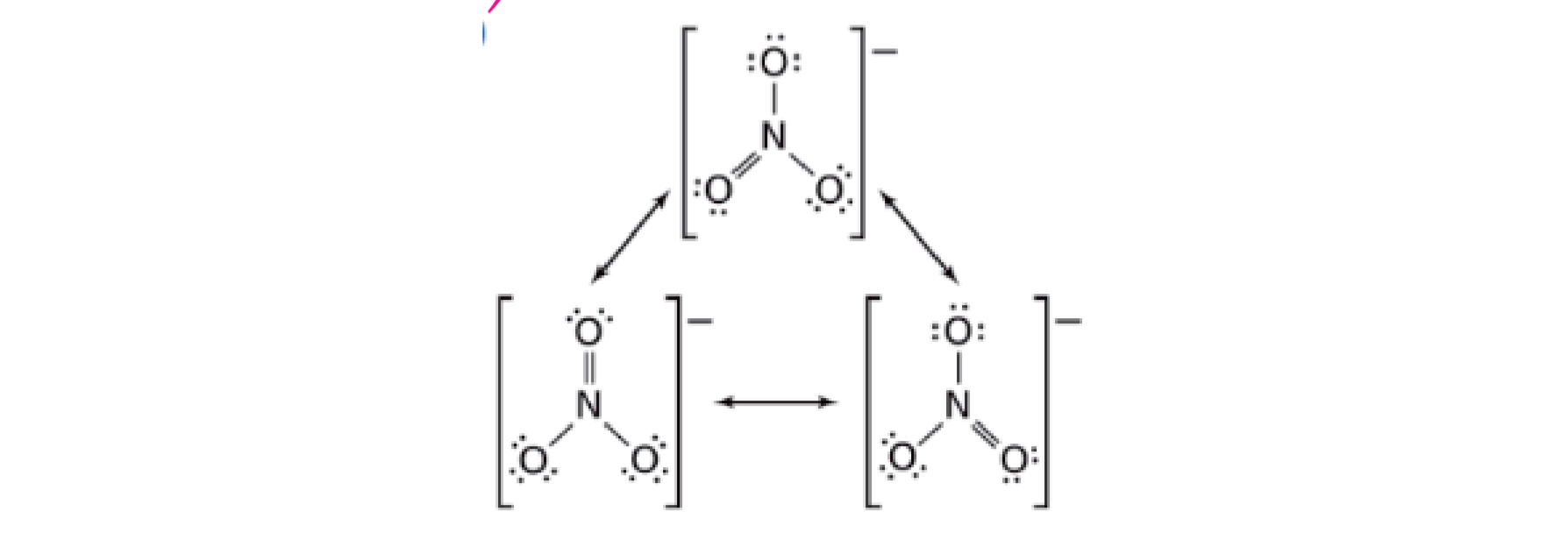
2.4.4 共振 - Resonance
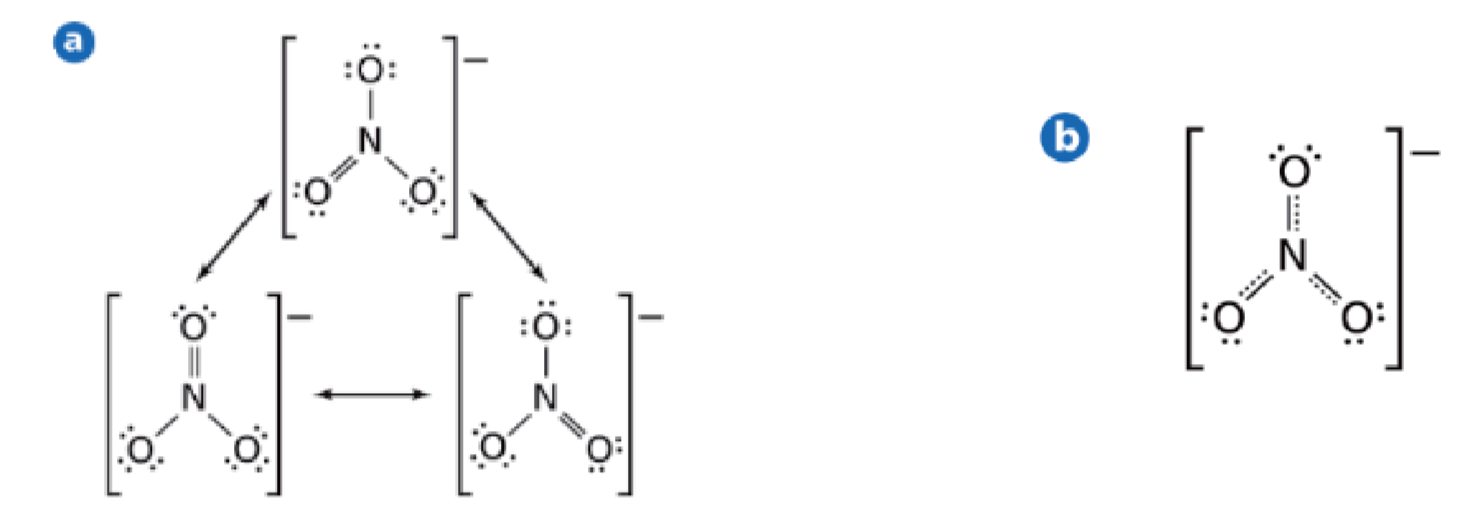
简单来说,就是一个路易斯结构无法表达,需要多个来表达。在共振结构之间用双箭头“←→”联系,以表示它们的共振关系。
臭氧、苯、烯丙基的共振结构(不过这个和考试要求的写法不太一样,看看就好)
硝酸根:
重要:共振结构中,每根键都是一样的
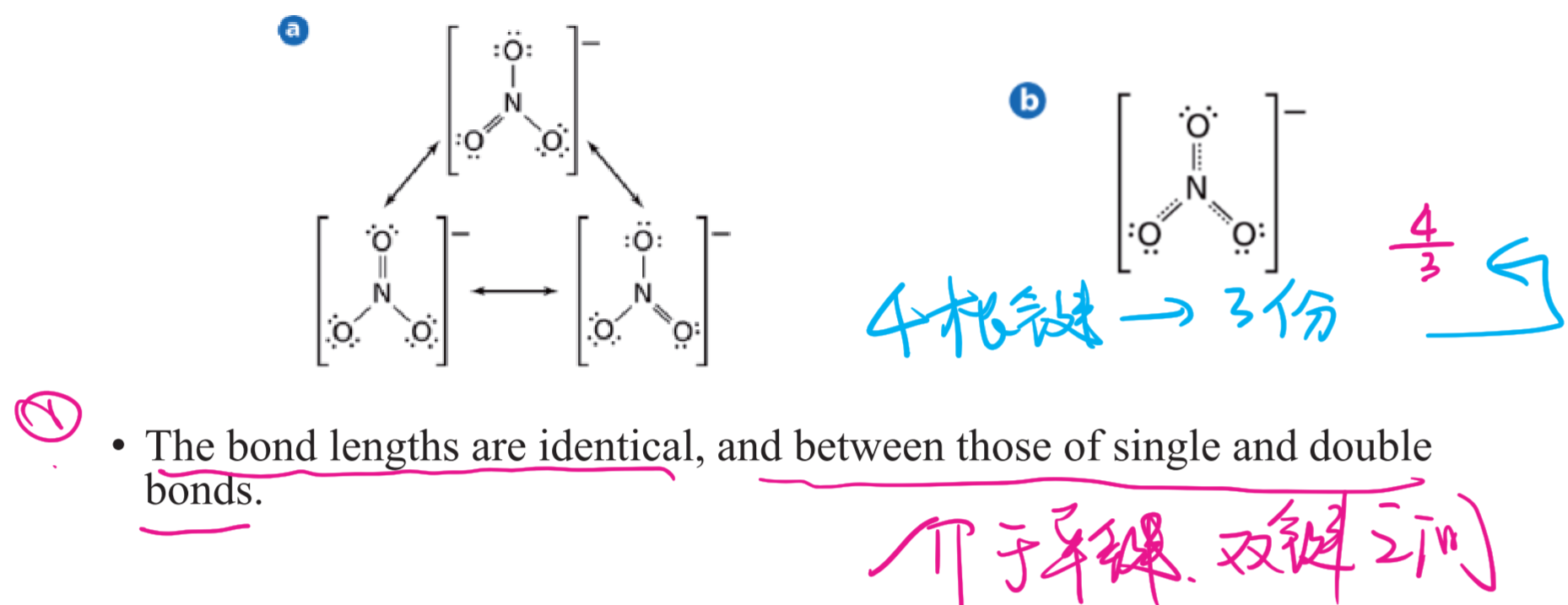
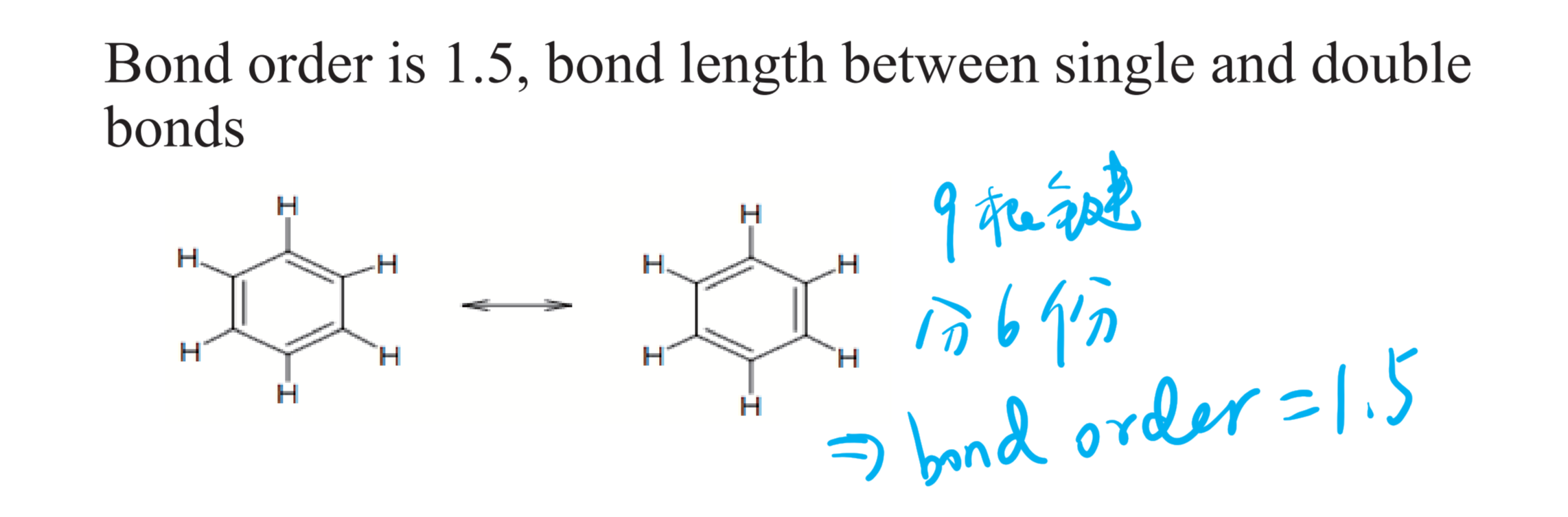
2.4.5 键级 - Bond Order
人话:所有的键平均分在每个需要放键的地方。举个例子:
$$
\text {Bond Order} (\ce{NO3-}) = \frac 4 3
$$
$$
\text {Bond Order} (\ce{C6H6}) = \frac 9 6 = 1.5
$$
2.4.6 一道很有意义的例题
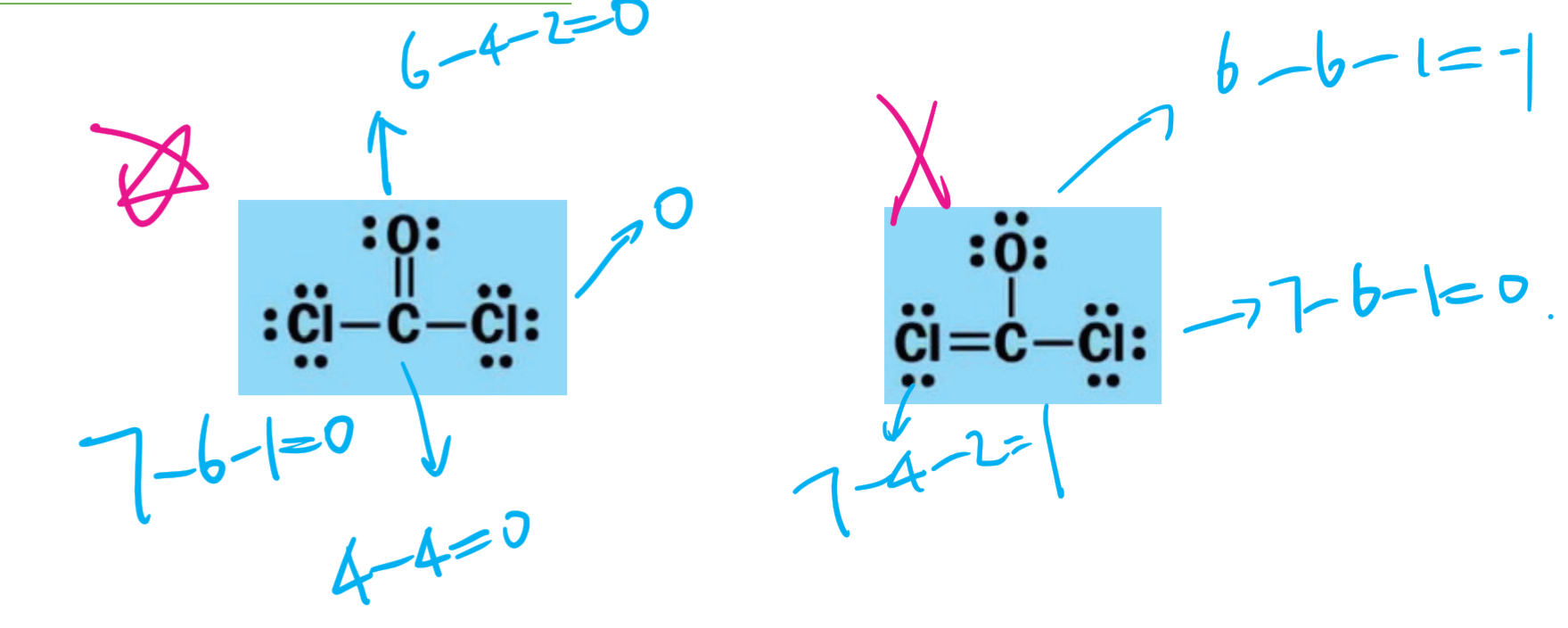
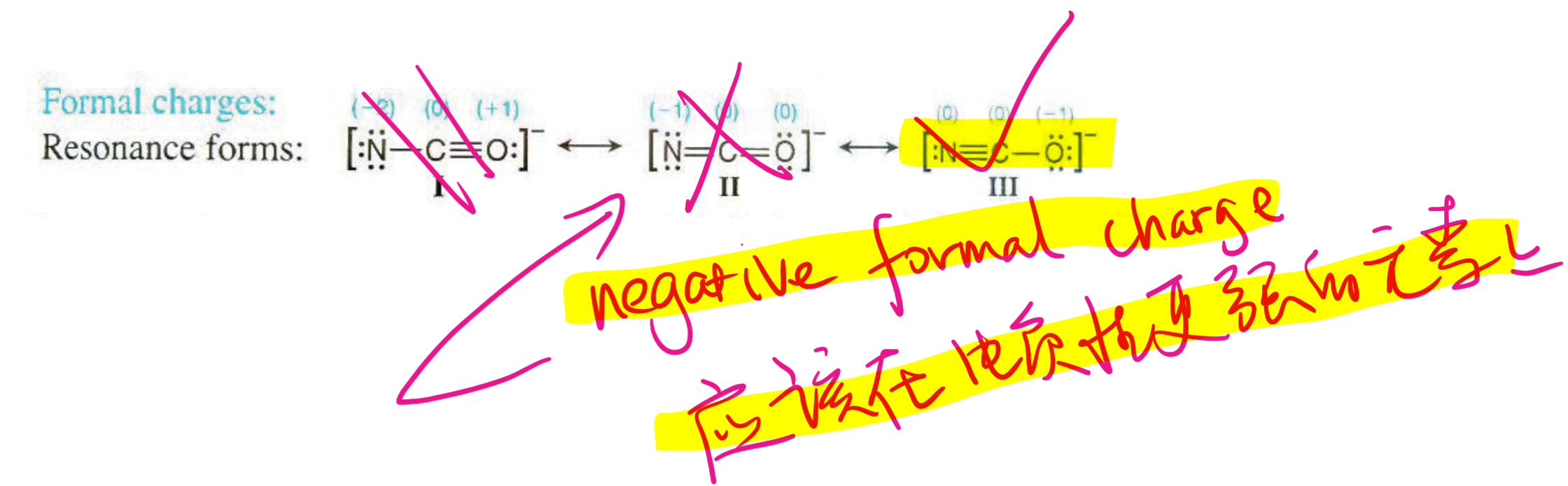
2.4.7 形式电荷 - Formal Charge
在化学上是指分配给分子中的一个原子的电荷,并假定所有化学键中的电子在原子之间均等共享,而无论相对电负性如何。当确定某个分子的最佳Lewis结构(或主要共振结构)时,所选结构使得每个原子上的形式电荷尽可能接近于零。
计算:
$$
FC(\text {Formal Charge}) = V - N - \text {Bonds}
$$
其中,$V$代表价电子数 (Valence Electrons),$N$代表未成键电子数 (Unbounded electrons),$\text {Bonds}$代表键的个数。
2.4.8 形式电荷的应用
负的形式电荷 (Negative FC) 应该在电负性更强的元素上 (Element with greater electronegativity)
Unit 3 分子间作用力与性质 - Intermolecular Forces and Properties
3.1 分子间作用力 - Intermolecular Forces
3.1.0 分子间作用力的性质
分子间作用力越大,物质熔沸点越高
3.1.1 可极化性 - Polarizability
在这里可以理解为:电子越多,polarizability越高
3.1.2 伦敦色散力 - London Dispersion Forces
3.1.2.1 成因
成因:分子有很多电子,电子一直在动,所以电子云可以产生瞬间偶极,这些偶极间的作用力称为伦敦色散力
3.1.2.2 特点
特点:所有分子都有
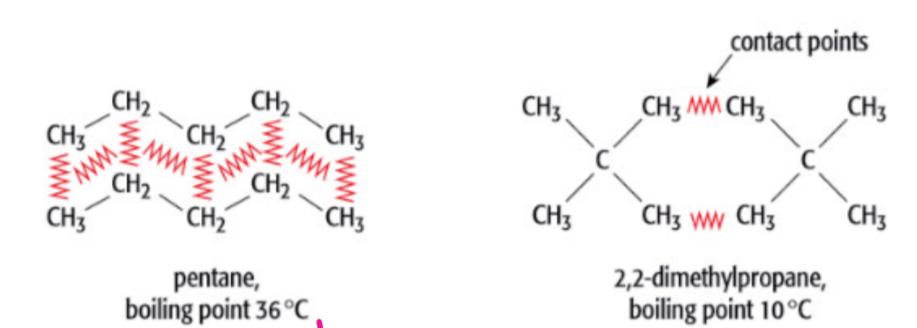
3.1.2.3 影响因素
- 电子数 / 式量
$$
\begin{aligned}
&电子越多 \\
&\downarrow \\
&Polarizability \uparrow \\
&\downarrow \\
& 色散力\uparrow
\end{aligned}
$$ - 接触点,例子:
3.1.3 偶极偶极作用力 - Dipole-dipole Forces
3.1.3.1 成因
极性分子中的永久偶极间的作用力
3.1.3.2 特点
只有极性分子才有
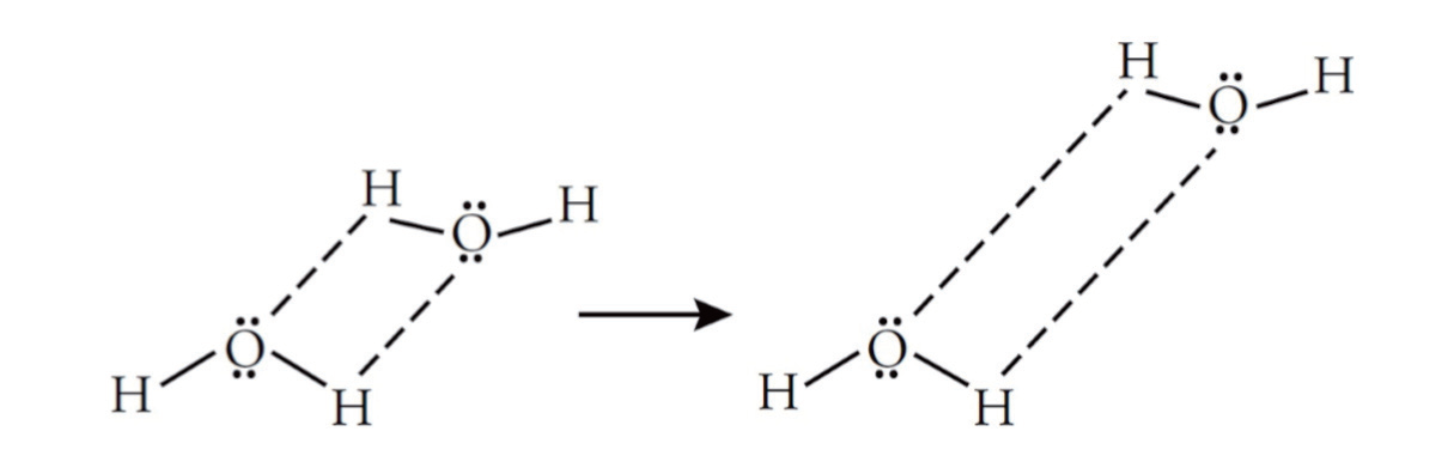
3.1.4 氢键 - Hydrogen Bond
- 属于偶极偶极作用力的一种,只不过特别强
- 形成条件(重要!!):
- $\ce{H}$直接连在$\ce {N, O, F}$(电负性大)上
- 形式是$\ce {X-H...Y}$
3.1.5 偶极诱导偶极作用力 - Dipole-induced Dipole Forces
极性分子诱导非极性分子产生偶极,诱导出来的偶极和极性分子的偶极之间的作用力,为偶极诱导偶极作用力
3.2 固体 - Solid
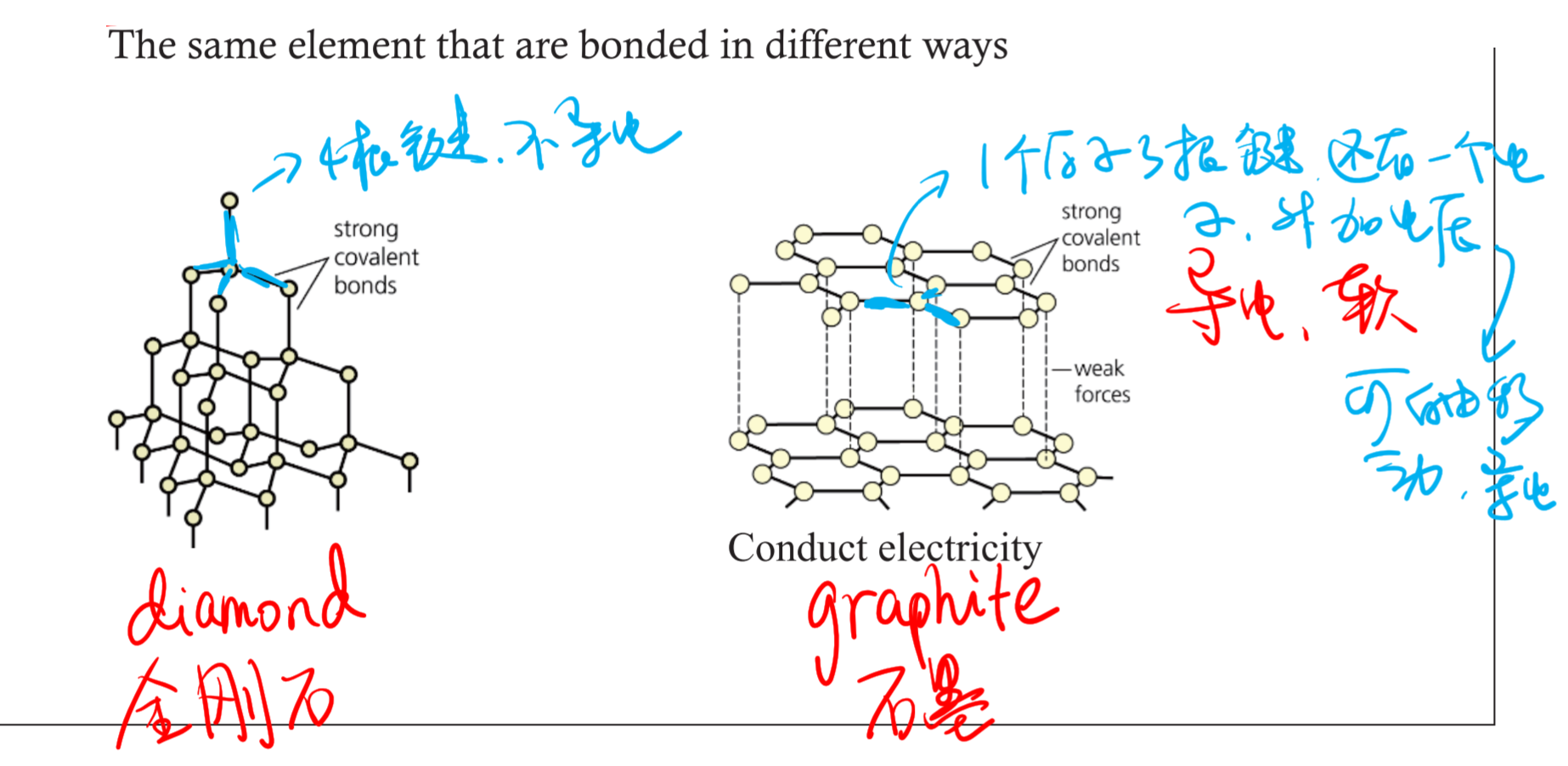
3.2.1 同素异形体 - Allotrope
$\ce C$:
- diamond 金刚石
- graphite 石墨
- $\ce{C60}$
3.2.2 晶体 - Crystal
| 晶体类型 | 金属晶体 | 离子晶体 | 分子晶体 | 原子晶体 |
|---|---|---|---|---|
| 英文 | Metallic Crystal | Ionic Crystal | Molecular Crystal | Atomic Crystal Covalent Network Network Solid |
| 定义 | 由金属键构成的晶体 | ...离子键... | 通过分子间作用力 形成的晶体 |
通过共价键形成的 具有空间网状结构的晶体 |
| 结构微粒 | 金属阳离子和电子 | 阴阳离子 | 分子 | 原子 |
| 微粒间作用力 | 金属键 | 离子键 | 分子间作用力 | 共价键 |
| 熔沸点 | 有高有低 | 一般高 | 较低 | 高 |
| 熔沸点举例 | $\ce{Na < Mg < Al}$ $\ce{+1<+2<+3}$ 根据金属键强弱 |
$\ce {NaCl < MgCl2 < Al2O3}$ | 式量越大 $\rightarrow$LDF越大 $\rightarrow$熔沸点越高 |
$\ce{C > SiC > Si}$ $键长:\ce{C-C < Si-C < Si-Si}$ |
3.3 气体 - Gas
3.3.1 理想气体 - Ideal Gas
三个条件:
- 忽略分子间作用力:there are no forces of attraction between the gas molecules in ideal gas.
- 忽略气体分子体积:molecules of an ideal gas occupy zero volume.
- 碰撞无能量损失:gas molecules are in constant motion, colliding with on another and with the walls of their container without losing any energy.
3.3.2 接近理想气体的状态
- 高温(T)低压(P):气体体积更大,分子大小相对更小,方便忽略
- 相同T.P.,分子相对质量越小,越接近:同理。
3.3.3 分子动理论 - Kinetic Molecular Theory
分子动能只与温度有关!!!
分子动能只与温度有关!!!
分子动能只与温度有关!!!
- 分子动能和压强无关!!!
- 分子动能和分子种类无关!!!
3.3.4 压缩,温度不变,压强变大,与分子动能无关的解释
在温度不变的情况下,压缩气体体积,体积变小,但是因为温度不变,所以分子动能不变,下面来解释一下为什么压强会变大。
假设分子平均运动速率为$u$,假设容器为正方体,分子在$x,y,z$三个方向做直线运动。因为是理想气体,所以气体分子和容器壁的碰撞时完全弹性碰撞,无能量损失。所以$\Delta u = u - (-u) = 2u$. 假设在一个时刻,某个表面的分子密度为$\rho$,经过微元时间$\mathrm dt$完成碰撞,更具动能定理,列出如下方程:
$$
F\cdot \mathrm dt = \rho S m_0 \Delta u
$$
其中,$S$为容器壁面积,$m_0$为单个分子质量。化简等式:
$$
p\cdot \mathrm dt = \rho m_0 \Delta u
$$
$$
p = \frac {\rho m_0 \Delta u} {\mathrm dt}
$$
整个变化过程中,只有$\rho$变大了(因为体积变小了),所以压强变大。
注意:整个过程中,$u$没有变化,即分子平均动能没有变化,温度没有变化
3.3.5 分子动能和分子运动速率
$$
K = \frac 1 2 m v^2
$$
所以,相同温度下分子A与分子B的速率之比为他们摩尔质量之比开方的倒数。
$$
\frac {v_A} {v_B} = \sqrt {\frac {M_B} {M_A}}
$$
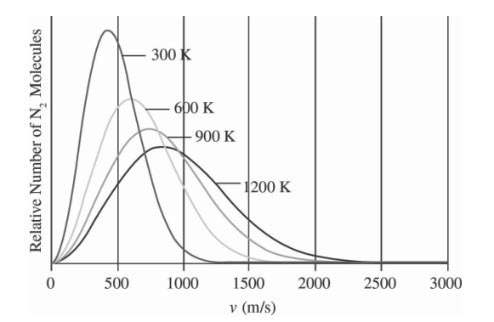
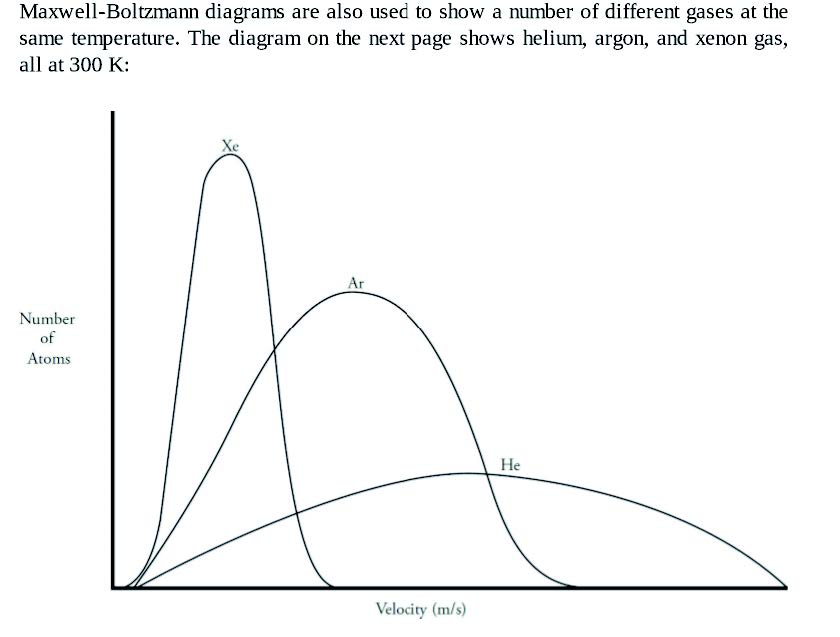
3.3.6 麦克斯韦-玻尔兹曼分布 - Maxwell-Bolzmann Diagram
相同物质,不同温度下,平均分子动能越高,峰值越低(统计学规律,而且分子总量相同):
不同物质,相同温度,摩尔质量越低,平均分子动能越高:
3.3.7 几种压强单位
$$
1 ~\text{atm} = 760 ~\text{mmHg} = 760 ~\text{torr}
$$
3.3.8 理想气体方程 - Ideal Gas Equation
$$
pV = nRT
$$
记得$R$值选择时要看好单位
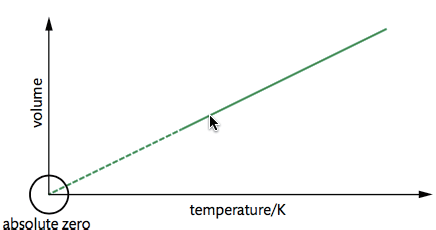
3.3.9 几条气体定律
- Charles's Law
$$
\frac {V_1} {V_2} = \frac {T_1} {T_2}
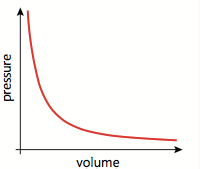
$$ - Boyle's Law
$$
p_1 V_1 = p_2 V_2
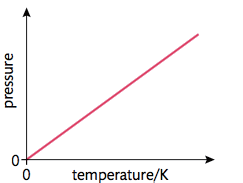
$$ - Gay-Lussac's Law
$$
\frac {p_1} {p_2} = \frac {T_1} {T_2}
$$ - Avogadro's Law
$$
\frac {V_1} {V_2} = \frac {n_1} {n_2}
$$



3.3.10 真实气体 - Real Gas
和理想气体相反:
- 存在分子间作用力
- 分子大小不可忽略
Ideal > Real:分子间吸引力
Ideal < Real:分子大小不可忽律
3.3.11 分压 - Partial Pressure
$$
p_{total} = p_1 + p_2 + \cdots
$$
举个例子:排水法收集$\ce{O2}$的集气瓶里:
$$
p = p_{\ce{O2}} + p_{\ce{H2O}}
$$
3.3.12 蒸汽压
拿水的蒸发举例(其他液体一样),就是水蒸气对水面的分压。
3.3.13 蒸汽压的影响因素
- 同一物质,$T \uparrow$,$\Rightarrow ~ p \uparrow$
- 不同物质相同温度,$\boldsymbol{IMF} \downarrow$(就是沸点越低),$\Rightarrow ~ p \uparrow$
3.4 三态变化
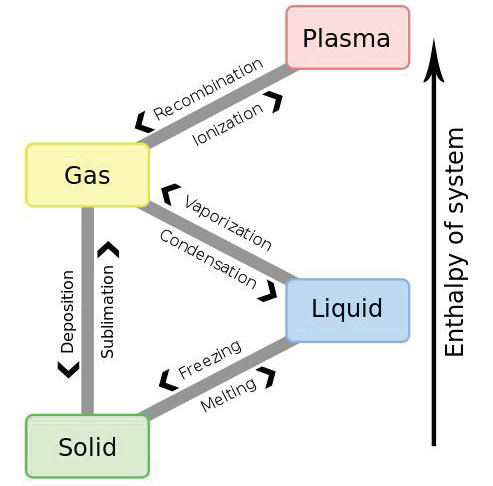
3.4.0 术语 - Terminology
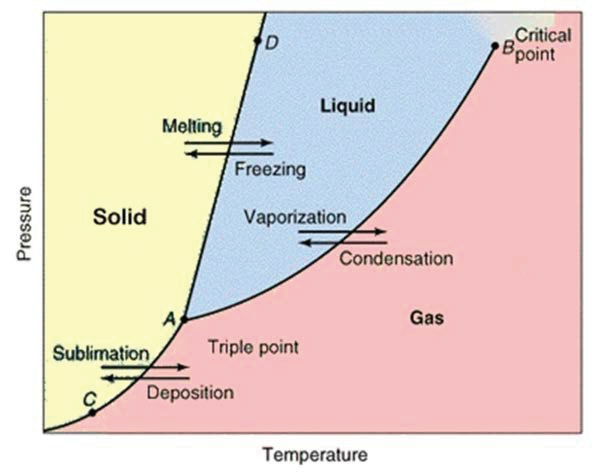
3.4.1 三相图 - Phase Diagram
- 横坐标温度,纵坐标气压
- 要做到:
- 知道一个状态下的熔沸点
- 给出一个点知道状态
- 中间有一个Triple Point,三种状态共存
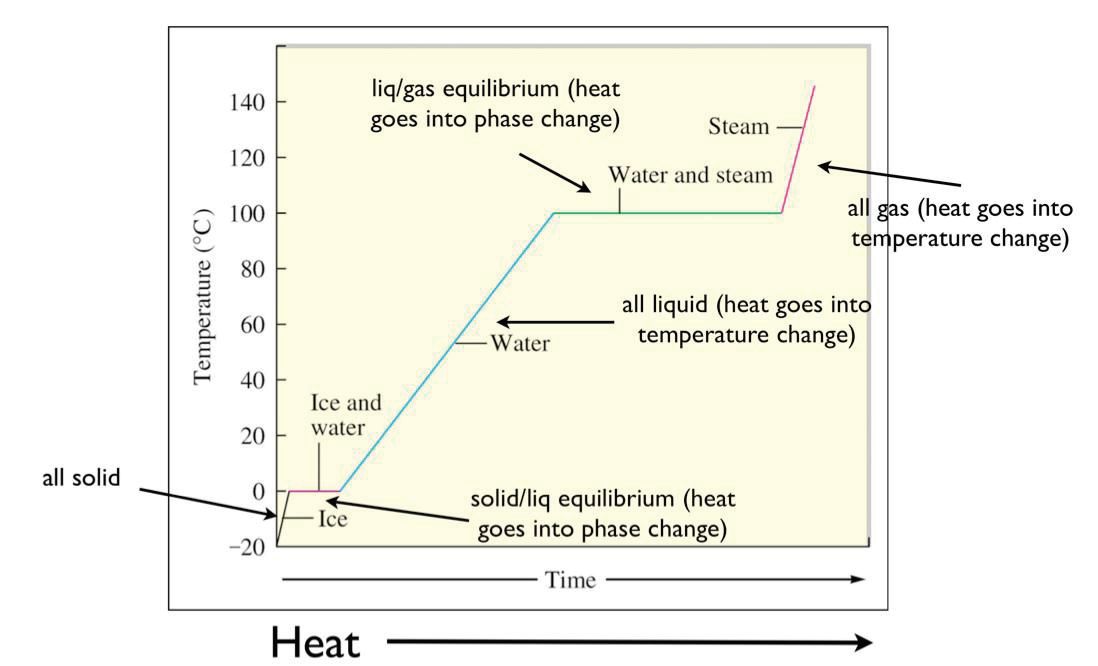
3.4.2 加热(冷却)曲线 - Heating(Cooling) Curve
冷却曲线就反过来。
3.4.3 汽(熔)化热 - Heat of Vaporization (Fusion)
- Heat of Fusion: 熔化热
- 本质:弱化分子间作用力
- Heat of Vaporization: 汽化热
- 本质:完全克服分子间作用力
所以,汽化热 > 熔化热
3.4.4 汽化热的大小比较
汽化是克服分子间作用力,所以IMF越强,汽化热越高。
3.4.5 沸腾
沸腾就是蒸汽压等于大气压
$$
p_{vapor} = p_{atm}
$$
3.5 溶液 - Solution
3.5.1 摩尔浓度 ($M$) - Molarity
$$
M = \frac n V
$$
单位:$\text{mol/L}$,或者写作$M$
3.5.2 质量摩尔浓度 ($m$) - Molality
$$
m = \frac {溶质摩尔数} {溶剂质量}
$$
单位:$\text{mol/kg}$
3.5.3 摩尔分数 - Mole Fraction
$$
x_B = \frac {n_b} n = \frac {n_b} {n_a + n_b}
$$
$n_b$是溶质的摩尔数,$n$是溶液中的总摩尔数。无量纲。
3.5.4 过饱和溶液 - Supersaturated Solution
- 溶质比饱和溶液还要多
- 高温的时候配置,慢慢冷却
- 很不稳定
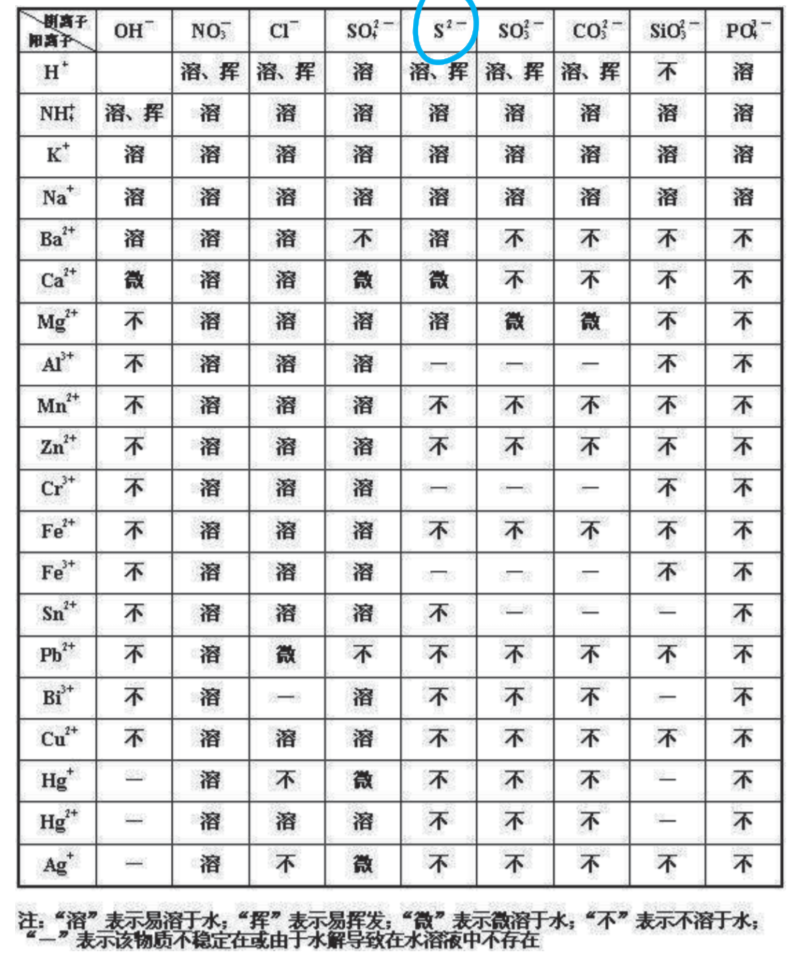
3.5.5 溶解度 - Solubility
- 内因:相似相溶(极性、非极性),有氢键的话更强
- 外因:
- 固体:$T \uparrow~\Rightarrow ~ s \uparrow$
- 气体:$T\uparrow ~\Rightarrow ~ s \downarrow$, $p \uparrow ~\Rightarrow ~ s \uparrow$
3.5.6 溶解度表 - Solubility Table
3.5.7 溶解度的应用
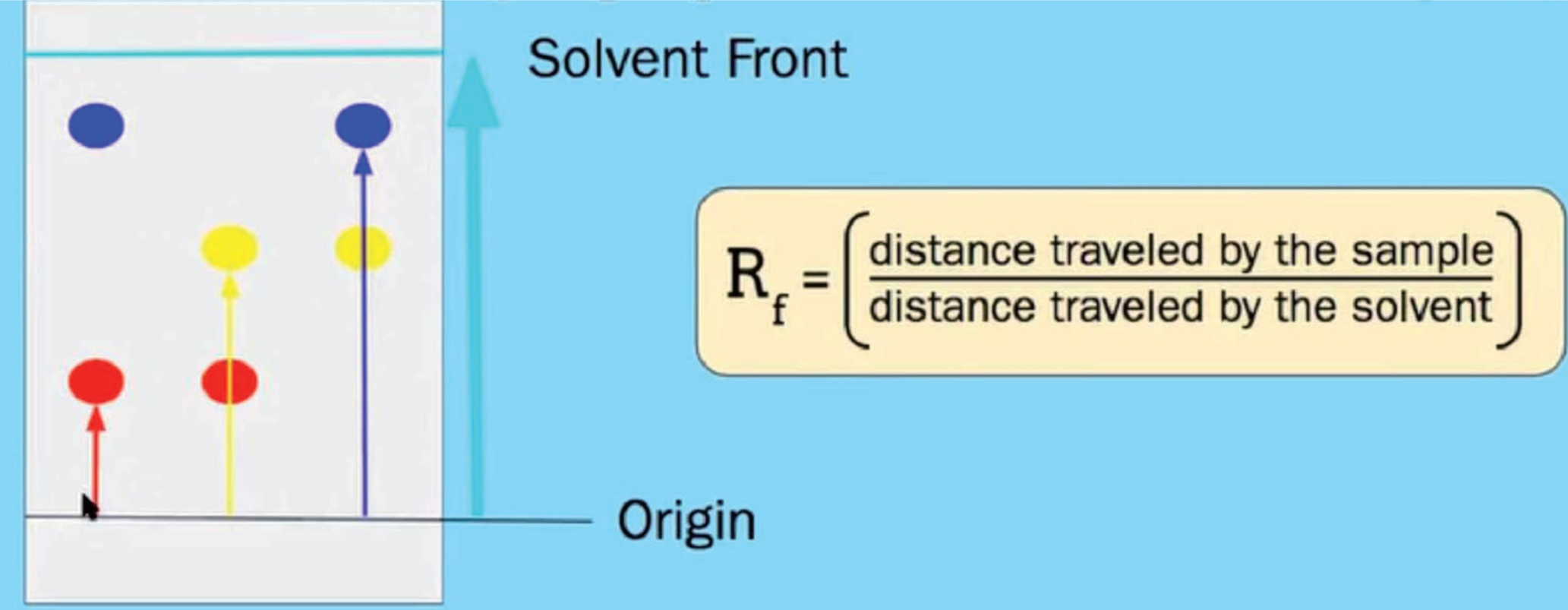
3.5.7.1 纸层析法 - Paper Chromatography
用途
分离色素
原理
- 溶解度大,扩散速度快,在上面析出
- 溶解度小,扩散速度慢,在下面析出
$R_f$值 - Rentention Factor
$$
R_f = \frac {色素移动的距离} {溶液移动的最远距离}
$$
每种物质的$R_f$是一样的,所以可以用来确定成分。
3.5.7.2 分光光度计 - Spectrophotometer
用途
测量溶液的浓度
原理 - Beer's Law
$$
A = abc
$$
- $A$: Absorbance 吸收的光
- $a$: Molar Absorptivity分子的吸收光的能力,由分子种类决定
- $b$: 比色皿 (cuvette) 的长度,就是光穿过的长度
- $v$: 溶液的浓度
应用的条件
- 溶质要对这个波长的光有吸收
- 物质的唯一性:只有我们要测的溶质对这个波长的光有吸收
Unit 4 - Chemical Reaction
4.1 化学反应和离子反应方程式 - Chemical & Ionic Equations
4.1.1 几种化学反应类型
- 化合反应 Sythesis Reactions
- 分解反应 Decomposition Reactions
- 置换反应 Single Replacement Reactions
- 燃烧反应 Combustion
- 酸碱中和 Acid-Base Reactions
- 氧化还原反应 Oxidation-Reduction (Redox) Reactions
- 复分解反应 Precipitation Reactions (Double Replacement)
4.1.2 离子反应方程式 - Ionic Equations
- 写:明确写出有关反应的化学方程式。
- 拆:
- 可溶性的强电解质(强酸、强碱、可溶性盐)一律用离子符号表示,其它难溶的物质.难电离的物质、气体、氧化物,水等仍用化学式表示。
- 对于微溶物质来说在离子反应中通常以离子形式存在(溶液中),但是如果是在浊液里则需要写出完整的化学式,例如,石灰水中的氢氧化钙写离子符号,石灰乳中的氢氧化钙用化学式表示。浓硫酸中由于存在的主要是硫酸分子,也书写化学式。浓硝酸、盐酸是完全电离的,所以写离子式。
- 删:删去方程式两边相同的离子和分子。
- 查:检查式子两边的各种原子的个数及电荷数是否相等,是否配平,还要看所得式子化学计量数是不是最简整数比,若不是,要化成最简整数比。
4.2 Chemical Equations & Calculations
4.2.1 限量试剂 - Limiting Reagent
人话:就是量不够,少量。
4.2.2 产率 - Yield Percentage
$$
\text{Yield Percentage} = \frac {实际收集} {理论值} \times 100 \%
$$
4.3 氧化还原 - Redox Reaction
4.3.1 化合价 - Oxidation Numbers
- 单质化合价为0
- IA族元素在化合物中化合价+1
- IIA族元素在化合物中化合价+2
- $\text{H}$在和金属形成氢化物时显-1价
- $\text{O}$在过氧化物中显-1价
4.3.2 氧化还原反应 - Redox Reactions
- 氧化剂化合价下降,被还原,发生还原反应,得电子
- 还原剂化合价上升,被氧化,发生氧化反应,失电子
4.3.3 半反应 - Half-Reactions
注意国外的写法,貌似只写$+e^-$
$$
\ce {Zn -> Zn^2+ + 2 e-}
$$
$$
\ce {Cu^2+ + 2e- -> Cu}
$$
4.3.4 氧化还原滴定 - Redox Titration
例子(不止下面这个反应):
$$
\ce {16H+ + 5C2O4^2- + 2MnO4- -> 2Mn2+ + 8H2O(l) + 5CO2(g)}
$$
$$
紫红色 \rightarrow 无色
$$
Unit 5 化学动力学 - Chemical Kinetics
5.1 化学动力学理论 - Theories of Chemical Kinetics & Reaction Rate
5.1.1 碰撞理论 - Collision Theory
三个条件:
- Particle must collide 必须碰撞
- Sufficient Energy 足够的能量
- Correct Orientation 正确的碰撞角度
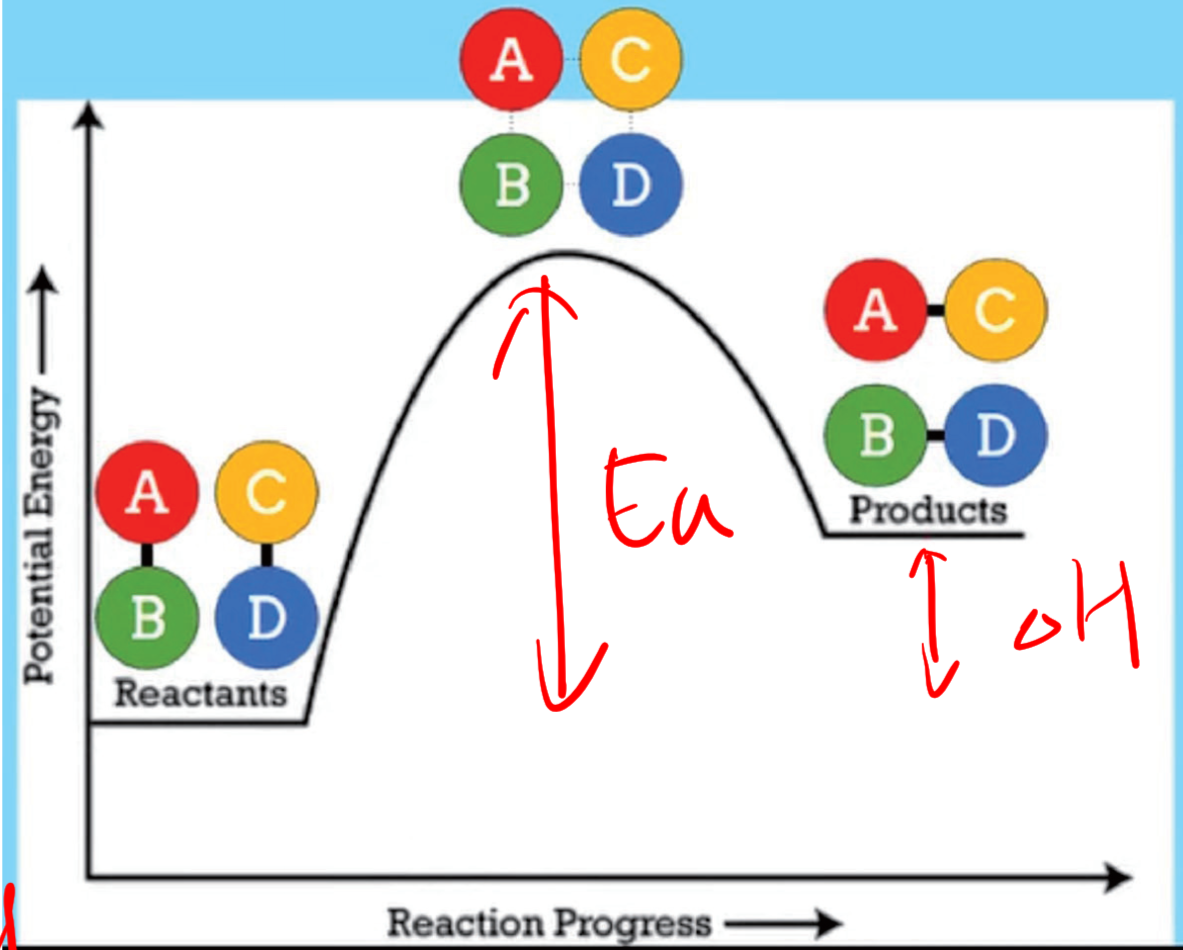
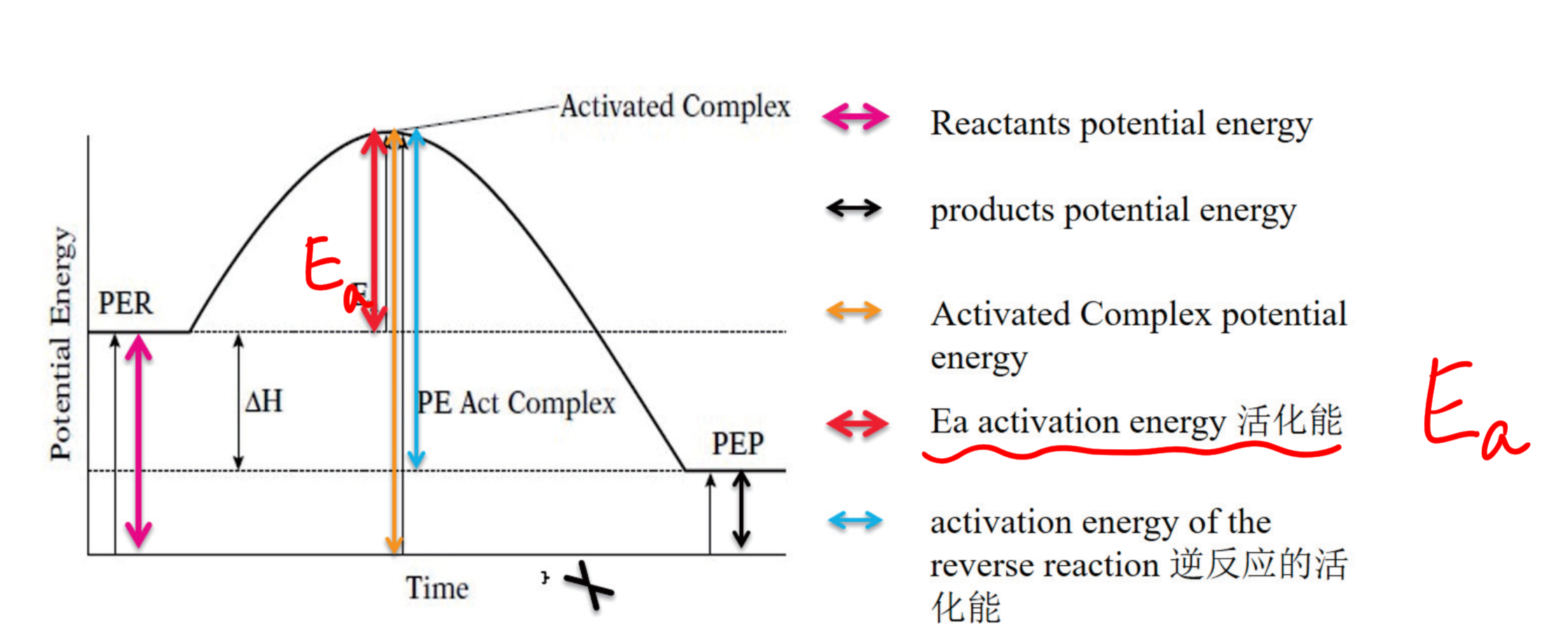
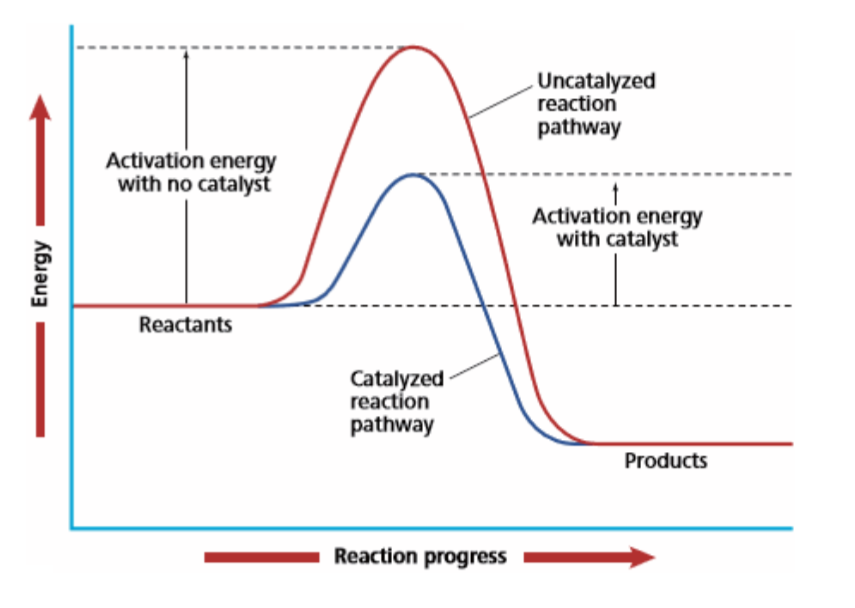
5.1.2 过渡态理论 - Transition State Theory
过渡态理论即活化络合物理论,(transition-state theory)。过渡态:以量子力学对反应过程中的能量变化的研究为依据,认为从反应物到生成物之间形成了势能较高的活化络合物,活化络合物所处的状态叫过渡态。
活化能:$E_a$, Activation Energy
注意:正反应和逆反应的活化能不同!!!
$$
E_a \uparrow ~ \Rightarrow ~ \text {Rate} \downarrow
$$
$$
E_a \downarrow ~ \Rightarrow ~ \text {Rate} \uparrow
$$
活化能和反应速率反向变化。
5.2 反应速率 - Reaction Rate
本章节笔记摘自网课期间市教委网课的笔记。
$$
化学反应条件
\begin{cases}
反应快慢 \rightarrow 化学反应速率问题 \\ 反应程度 \rightarrow 化学平衡问题
\end{cases}
$$
$$
研究化学反应快慢目的
\begin{cases}
认识化学反应快慢规律 \\ 科学调控反应快慢
\end{cases}
$$
5.2.1 化学反应速率
- 化学反应 有快有慢
- 不同的化学反应 进行的快慢往往不同
- 统一化学反应在 不用条件 下进行的快慢不同
- 可以用 化学反应速率 来表示化学反应进行的快慢
- 化学反应速率是 单位时间 内反应物 浓度 的减少量或生成物浓度的增加量来表示
- 表达式
$$ v = \frac {\Delta c}{\Delta t} $$ - 单位:$\text {mol/(L }\cdot \text{ s)或mol/(L } \cdot \text { min)}$
- 各物质化学反应速率之比等于化学方程式当中各物质前面的化学计量数之比
- 对于任意一个化学反应:
$$\ce {mA + nB -> pC + qD}$$
$$v(A) : v(B) : v(C) : v(D) = m : n : p : q$$ - 对同一化学反应,用不同物质的浓度变化所表示的化学反应速率的数值是否一定不相同?为什么?
不一定。同一个化学反应中,反应物浓度的减少和生成物浓度的增加都是按照化学方程式中各物质的计量数关系成比例变化的。 - 化学反应速率测定的方法
$$
化学反应速率的测定方法 \begin{cases}
化学方法 \begin{cases}
利用化学原理直接测定物质浓度 \\ 停止反应方法:骤冷、冲稀等
\end{cases} \\ 物理方法 \begin{cases}
利用物理性质与浓度之间的相关性 \\ 量气法、分光光路法、电导率法
\end{cases}
\end{cases}
$$
5.2.2 影响化学反应速率的因素
- 反应物的性质
- 浓度
- 温度
- 压强
- 催化剂
- 其他
- 反应物的性质是决定化学反应速率的根本原因
浓度、温度等因素一会影响化学反应速率的大小
- 选择研究对象 -- 一个确定的化学反应
- 有明显的实验现象、易于观察
- 速率应该始终
- 安全、无污染,方便易行
- 选择试验方法:控制变量法
- 实验研究
$$\mathrm{Na}_{2} \mathrm{S}_{2} \mathrm{O}_{3}+\mathrm{H}_{2} \mathrm{SO}_{4} \rightarrow \mathrm{S} \downarrow+\mathrm{SO}_{2}+\mathrm{Na}_{2} \mathrm{SO}_{4}+\mathrm{H}_{2} \mathrm{O}$$
浓度对化学反应速率影响的实验研究
- 结论
在其他条件不变时,增大反应物的浓度,化学反应速率加快。
在其他条件不变时,减小反应物的浓度,化学反应速率减慢。
固体不考虑在内。 - 应用
日常生活中为了延长食品保质期,一些食品采用充N2包装或加入脱氧剂,其目的都是为了减小O2的浓度,减慢食品氧化变质速率。
理论解释:
$$
浓度 \uparrow~~ \Rightarrow 碰撞的频率 \uparrow~~ \Rightarrow v \uparrow
$$
颗粒大小(固体表面积)对化学反应速率影响的研究
- 对相同质量的固体物质而言, 颗粒越大,固体表面积越小; 颗粒越小,固体表面积越大。
- 结论
在其他条件不变时,增大固体颗粒的表面积,化学反应速率加快。
在其他条件不变时,减小固体颗粒的表面积,化学反应速率减慢。 - 应用:煤粉发电、粉尘爆炸
温度对化学反应速率影响的研究
结论:在其他条件不变时,升高反应温度,化学反应速率加快。降低反应温度,化学反应速率减慢。
碰撞理论的解释:
$$
T \uparrow~~\Rightarrow 分子动能KE \uparrow~~\Rightarrow 碰撞频率 \uparrow ~~\Rightarrow v \uparrow
$$
过渡态理论的解释:
$$
T \uparrow ~~\Rightarrow KE \uparrow ~~ \Rightarrow 更多能量克服E_a \Rightarrow v \uparrow
$$
$\ce {Zn}$和稀硫酸反应速率先变大后变小,是因为这个反应是放热反应,速率先变大,后因为反应物的浓度变小,速率变小。
催化剂对化学反应速率影响的实验研究
- 研究对象:$\ce {2H2O2 ->[MnO2]2H2O + O2 ^}$
- 实验:在双氧水中加入二氧化锰
- 现象:没有加入$\ce {MnO2}$粉末的双氧水试管中只有少量气泡出现,不能使带火星的木条复燃;加入$\ce{MnO2}$粉末后试管内产生大量气泡,带火星的木条复燃
- 结论:催化剂可以有效地提高化学反应速率
$$
催化剂与生活
\begin{cases}
现代化学工业生产: \ce {2SO2 + O2 <=>[V2O5][\Delta] 2SO3} \\
生物体中化学反应 \\
环境保护催化剂
\end{cases}
$$
理论解释:降低活化能$E_a$
结论:
- 加入催化剂改变了反应的途径,降低了反应所需要的能量,从而加快化学反应速率。
- 加入催化剂不会改变该化学反应的热效应。
$$
催化剂的基本知识 \begin{cases}
催化剂的研究与开发 \\ 催化剂具有选择性 \\ 催化剂的活性温度 \\ 催化剂中毒
\end{cases}
$$
压强对化学反应速率的影响
结论:对于有气态物质参加的反应,在其它条件不变时增大压强,化学反应速率加快;减小压强,化学反应速率减慢。
5.3 速率方程 - Rate Law
5.3.0 速率方程
对于一个反应
$$
\ce {A + 2B + C -> D}
$$
Rate Law:
$$
\text{Rate} = k[\text A]^x [\text B]^y [\text C]^z
$$
其中:
- $k$是速率常数 Rate Constant,不同反应有不同的速率常数,速率常数与反应温度、反应介质(溶剂)、催化剂等有关,甚至会随反应器的形状、性质而异。与浓度无关,但受温度、催化剂、固体表面性质等因素的影响。但是,和浓度无关!!
- $[\text A], [\text B], [\text C]$是浓度
- $x, y, z$是需要我们求解的反应级数 Reaction Orders
5.3.1 反应级数 - Reaction Orders
由上一小节的论述,我们已经大概知道了什么是反应级数和速率方程(大概)。接下来我们要细说一下反应级数。现在我们控制变量,保证其他都不变,只考虑$[\text A]$和$x$.
- $x = 1$: 一级反应,First Order Reaction:
$$
\text {Rate} \propto [\text A]
$$ - $x = 2$: 二级反应,Second Order Reaction:
$$
\text {Rate} \propto [\text A] ^ 2
$$ - $x = 0$: 零级反应,Zero Order Reaction: 反应速率与$[\text A]$无关
Overall Order,总反应级数,在这里就是:
$$
x + y + z
$$
5.3.2 反应常数 - Rate Constant
注意单位!!(直接将式子中的计算出来即可。注意:零级反应$[\text A]^0$无量纲
$k$与$T$相关。$T\uparrow~~\Rightarrow k \uparrow$
5.4 积分速率方程 - Integrated Rate Law
注:这里只考虑一个浓度变量。
5.4.1 一级反应 - The First Order Reaction
结论:
$$
\ln [\text A]_t - \ln [\text A]_0 = -kt
$$
推导:
$$
\begin{cases}
\text {Rate} = k[\text A] \\ \text {Rate} = \displaystyle \frac {\mathrm d[\text A]} {\mathrm dt}
\end{cases} \Rightarrow \frac {\mathrm d [\text A]} {[\text A]} = -k \mathrm dt
$$
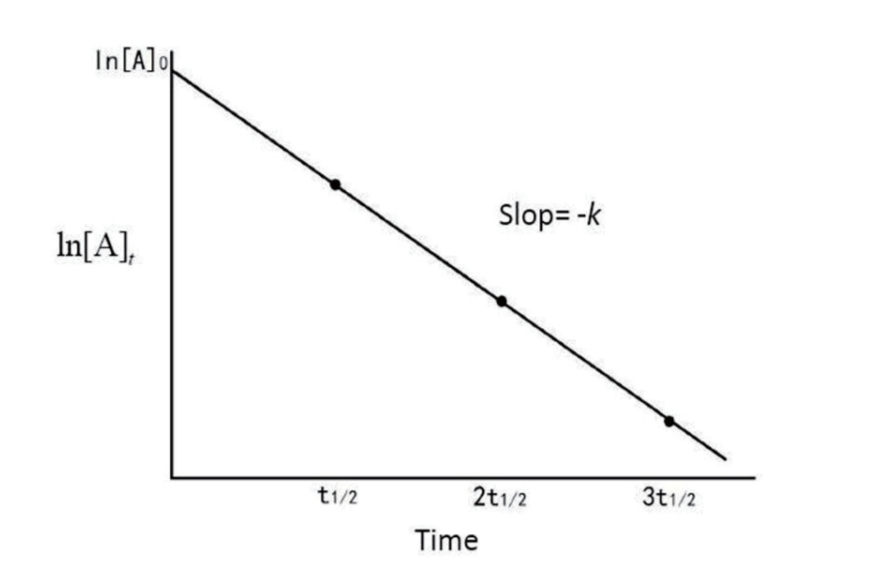
5.4.2 一级反应的半衰期判断依据
如果一种物质在一个反应中的反应级数为$1$,那么这种物质在这种反应当中的半衰期是常数。推导:
$$
-kt_{1/2} = \ln\frac 1 2 [\text A]_0 - \ln [\text A]_0 = \ln \frac 1 2
$$
$$
t_{1/2} = \frac {\ln 2} k
$$
5.4.3 一级反应的图像判断依据
$\ln [\text A]_t$与$t$成线性关系:
$$
\ln [\text A]_t = -kt + \ln [\text A]_0
$$
5.4.4 二级反应 - Second Order Reaction
结论:
$$
\frac 1 {[\text A]_t} - \frac 1 {[\text A]_0} = kt
$$
推导:
$$
\begin{cases}
\text {Rate} = k[\text A]^2 \\ \text {Rate} = \displaystyle \frac {\mathrm d[\text A]} {\mathrm dt}
\end{cases} \Rightarrow \frac {\mathrm d [\text A]} {[\text A]^2} = -k \mathrm dt
$$
5.4.5 二级反应的图像判断依据
$\displaystyle \frac 1 {[\text A]_t}$与$t$成线性关系:
$$
\frac 1 {[\text A]_t} = kt + \frac 1 {[\text A]_0}
$$
5.4.6 零级反应 - Zero Order Reaction
反应速率恒定:
$$
\text {Rate} = k
$$
5.4.7 零级反应的图像判断依据
$[\text A]_t$与$t$成线性关系:
$$
[\text A]_t = [\text A]_0 - kt
$$
5.5 反应机理 - Reaction Mechanisms
5.5.1 基元反应 - Elementary Reaction
基元反应是指在反应中一步直接转化为产物的反应,又称为简单反应。 化学反应式多数情况下不能说明反应的过程。现实中有的反应是一步完成,而多数的反应需要经历若干个步骤才能完成。基元反应的动力学规律符合质量作用定律,即:基元反应的化学反应速率与反应物的浓度数值相应方次乘积成正比;其方次即为各物质前面系数,均取正值。
5.5.2 总反应 - Overall Reaction
多个基元反应叠加形成
5.5.3 催化剂 - Catalyst
在多个基元反应中消耗又形成的东西,可以降低反应的活化能$E_a$
5.5.4 中间产物 - Intermediate
在多个基元反应中形成又消耗的东西。
5.5.5 慢反应 - Slow Reaction
慢反应速率决定总反应速率。(木桶原理)
5.5.6 不使用中间产物书写Rate Law的方法
在可以的情况下,Rate Law当中尽量不要出现中间产物。方法:可以运用慢反应上一步的可逆反应来实现,因为正反应速率等于逆反应速率。
举例:
$$
\begin{aligned}
&\text {Step 1} &\ce {A + B <=> C} & ~~~~~~~\text {fast equilibrium} \\
&\text {Step 2} &\ce {C + A -> D} & ~~~~~~~\text {slow} \\
&\text {Step 3} &\ce {C + D -> B + E} & ~~~~~~~\text {fast}
\end{aligned}
$$
根据慢反应:
$$
\text {Rate} = k_2 [\text C][\text A]
$$
根据第一步化学平衡:
$$
k_1 [\text A][\text B] = k_{-1} [\text C]
$$
所以
$$
\text {Rate} = \frac {k_1 k_2} {k_{-1}} [\text A]^2 [\text B] = k[\text A]^2 [\text B]
$$
5.5.7 活化能和慢反应
慢反应是活化能高的反应。
Unit 6 热力学 - Thermodynamics
6.1 热力学定律 - Laws of Thermodynamics
6.1.0 热力学第零定律 - Zeroth Law of Thermodynamics
处于热力学平衡状态的所有物质均具有某一共同的宏观物理性质。
6.1.1 热力学第一定律 - First Law of Thermodynamics
物体内能的增加等于物体吸收的热量和对物体所作的功的总和。即热量可以从一个物体传递到另一个物体,也可以与机械能或其他能量互相转换,但是在转换过程中,能量的总值保持不变。其推广和本质就是著名的能量守恒定律。
$$
\Delta U = Q + W
$$
6.1.2 热力学第二定律 - Second Law of Thermodynamics
- 克劳修斯表述: 不可能把热量从低温物体传向高温物体而不引起其它变化。
- 开尔文表述: 不可能制成一种循环动作的热机,从单一热源取热,使之完全变为功而不引起其它变化。
- 熵增加原理: 孤立系统的熵永不自动减少,熵在可逆过程中不变,在不可逆过程中增加。
6.1.3 热力学第三定律 - Third Law of Thermodynamics
热力学系统的熵在温度趋近于绝对零度时趋于定值。而对于完整晶体,这个定值为零。
6.1.4 比热容 - The Specific Heat Capacity of the Substance
通过比热容计算吸收的热量:
$$
Q = cm \Delta T
$$
6.1.5 量热计 - Calorimeter
6.2 化学反应中的能量变化
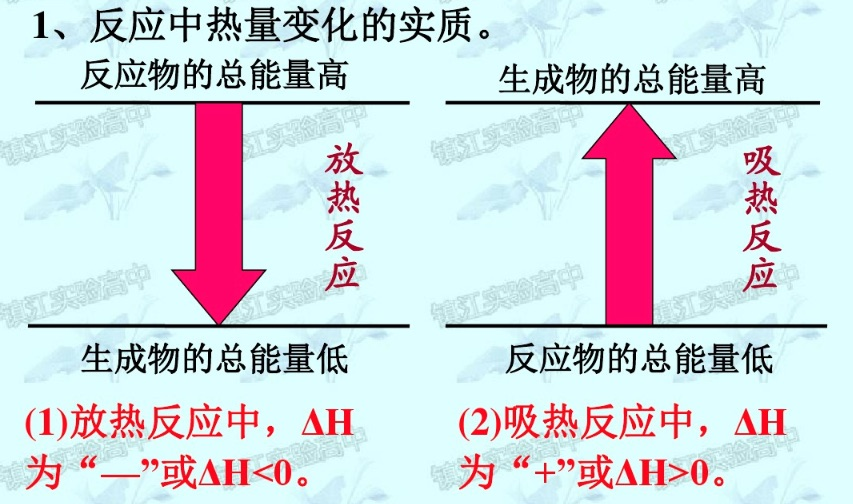
注:本节摘自网课期间记录的梁金纯老师化学课笔记。本节中的$E$可以理解为$H$
6.2.0 物质变化中的能量变化
- 能量守恒定律:能量在各种形式之间的转换和各个物体之间的转移过程中,各种形式的能量综合保持不变。
- 物理变化:
$$一定量的物质:E_g > E_l > E_s$$
$$\ce {H2O (l) -> H2O (g) - 44 kJ}$$
意义:$1 \text {mol}$液态水变成气体,吸收$44\text { kJ}$的热量。 - 化学变化:
$$\ce {C (s) + O2 (g) -> CO2 (g) + 393.5 kJ}$$
意义:$1 \text { mol}$的固态$\ce {C}$和$1 \text { mol}$的氧气反应,生成一摩尔的二氧化碳气体并放出393.5千焦的热量。要注意量、状态
6.2.1 化学反应中的热效应
$$\ce {C + O2 ->[点燃] CO2 + Q}~~~~放热反应$$
$$\ce {C + CO2 ->[加热] 2CO - Q}~~~~吸热反应$$
$$\ce {HCl + NaOH -> NaCl + H2O + Q}$$
- 化学能:只有在化学反应中才能释放出来的能量(热能、光能、......)
- 当化学反应中的能量变化表现为热量变化是:
- 对于放热反应:
$$\ce {\sum E_{反应物} -> \sum E_{生成物} + Q}$$
$$\sum E_{反应物} > \sum E_{生成物}$$ - 对于吸热反应:
$$\ce {\sum E_{反应物} -> \sum E_{生成物} - Q}$$
$$\sum E_{反应物} < \sum E_{生成物}$$
- 对于放热反应:
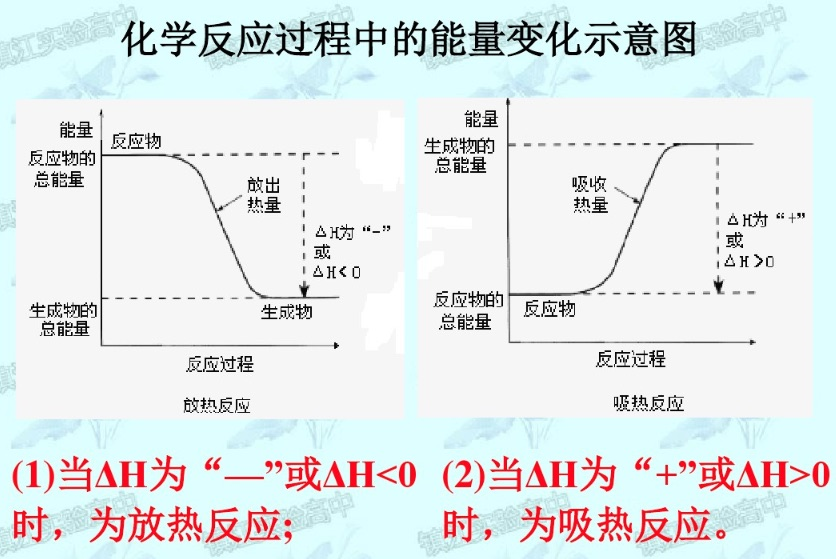
6.2.2 能量变化图
6.2.3 热化学反应方程式
表示化学反应中吸收或放出的能量的化学方程式
6.2.4 燃料的充分利用
$$
节约能源 \begin{cases}
燃料的充分燃烧 \begin{cases}
增大反应物的接触面积(固体反应物粉碎) \\ 过量的氧气 \\ \cdots
\end{cases} \\ 热能的充分利用 \begin{cases}
热量交换 \\ \cdots
\end{cases}
\end{cases}
$$
6.3 焓 - Enthalpy
6.3.1 状态函数 - State Function
只和初末状态有关!!
6.3.2 焓 - Enthalpy
体系的状态函数,用符号H表示。焓的定义式是:
$$
H = U + PV
$$
U是体系的内能,p是体系压强,V是体积。在一定状态下,体系的焓应有一定值,但现在无法测定焓的绝对值,对热力学来说重要的是焓的变化值,这是可以通过实验测量的。
6.3.3 焓变
焓变就是焓的变化量。
6.3.4 标准状态 - Standard State Condition
标准状况,需要和S.T.P.(标准状况)区分开来。那个是$273K$,这个是$298K$。
重要:这个状态下溶液浓度是$1M$
这个状态下的熵、焓、吉布斯自由能表示为:
$$
\Delta H ^ \circ, \Delta S ^ \circ, \Delta G ^ \circ
$$
6.4 反应焓变的计算
6.4.1 反应的焓变
$$
\Delta H = H_{生成物} - H_{反应物}
$$
单位:
$$
\Delta H: \text {kJ / mol}_{\text {rxn}}
$$
其实就是$\text {kJ}$,后面其实是热化学反应方程式的单位。
6.4.2 反应的吸热和放热
- $\Delta H > 0$:吸热反应,Endotherimic Reaction
- $\Delta H < 0$:放热反应,Exotherimic Reaction
6.4.3 生成焓 - Heat of Formation
生成焓是某温度下,用处于标准状态(Standard State Condition)的各种元素的最稳定单质(最稳定单质如液态溴、固态碘、石墨、白磷、斜方硫等。)生成标准状态下单位物质的量(1mol)某纯物质的热效应,也称生成热。表示为$\Delta H_f$
最稳定的单质的生成焓为$0$!!。原因:状态函数只和初末状态有关。$单质 \Rightarrow 单质$,所以$\Delta H_f = 0$
6.4.4 焓变的计算方法1 - 生成焓
$$
\Delta H = \sum \Delta H_{f, 生成物} - \sum \Delta H_{f, 反应物}
$$
记得在计算的时候乘上系数。
6.4.5 焓变的计算方法2 - 键能
$$
\Delta H = 断旧键吸收的能量 - 成新键释放的能量
$$
6.4.6 焓变的计算方法3 - 赫斯定律 - Hess's Law
赫斯定律,是1840年俄国化学家赫斯(Hess)研究了大量的热化学实验数据,他总结出一条规律:在定容或者定压的条件下,化学反应无论是一步完成还是分几步完成,其反应热是相等。
即反应的热效应只与系统始、末态有关,而与变化途径无关。赫斯定律是热力学第一定律的必然结果,因为H(或U)是状态函数,只要化学反应的始、末态确定,则△H或△U便是定值,而与通过什么具体途径来完成这一反应无关。
人话:其实就是可以叠加etc.
6.4.7 焓变的计算方法4 - 图像
见节6.2.4
9.1 熵与吉布斯自由能 - Entropy & Gibbs Free Energy
9.1.0 再论热力学第二定律
熵增定律
9.1.1 熵 - Entropy
描述混乱程度, Entropy is a measure of randomness or disorder
9.1.2 稳定与不稳定
| 能量 | 熵 ($S$) | 焓 ($H$) |
|---|---|---|
| 稳定 | $\uparrow$ | $\downarrow$ |
| 不稳定 | $\downarrow$ | $\uparrow$ |
9.1.3 熵变 - Change of Entropy
$$
\Delta S = \sum S_{生成物} - \sum S_{反应物}
$$
9.1.4 判断熵的高低的两条规则
- 根据状态:
$$
S_{固体} < S_{液体} < S_{气体}
$$
理解:固体分子排列更加规则,气体分子更加混乱。 - 气体摩尔数:
$$
反应后气体摩尔数\uparrow ~~~ \Rightarrow ~ S \uparrow
$$
9.1.5 吉布斯自由能判断反应是否能自发进行
- $\Delta G < 0$,反应自发进行,Thermodynamically Favored / spontaneous
- $\Delta G > 0$,反应不能自发进行,Thermodynamically Unfavored / Nonspontaneous
9.1.6 生成吉布斯自由能
标准生成吉布斯自由能是由标准状态下的稳定单质生成标准状态下1mol化合物时的吉布斯自由能变化。
类似于生成热(生成焓)
9.1.7 吉布斯自由能计算方法1 - 通过生成吉布斯自由能
$$
\Delta G ^ \circ = \sum \Delta G ^ \circ _ {f, 生成物} - \sum \Delta G ^ \circ _ {f, 反应物}
$$
类似于生成热(生成焓)
9.1.8 吉布斯自由能计算方法2 - $\Delta G = \Delta H - T \Delta S$
$$\Delta G = \Delta H - T \Delta S$$
9.1.9 $\Delta G = \Delta H - T \Delta S$的分析
- $\Delta H > 0, \Delta S < 0 \Rightarrow \Delta G > 0$,反应永远不能自发进行
- $\Delta H < 0, \Delta S > 0 \Rightarrow \Delta G < 0$,反应一定能自发进行
- $\Delta H > 0, \Delta S > 0$时,$T \uparrow$时有利于自发进行
- $\Delta H < 0, \Delta S < 0$时,$T \downarrow$时有利于自发进行
9.1.10 反应由xxx驱动 - Driven By
- $\Delta H < 0$,反应由焓变驱动
- $\Delta S > 0$,反应由熵变驱动
- $\Delta H < 0, \Delta S > 0$,反应由焓变和熵变同时驱动
9.1.11 吉布斯自由能计算方法3 - $\Delta G = -RT\ln K$
$$\Delta G = -RT \ln K$$
9.1.12 平衡常数$K$与反应是否能自发进行
- 平衡常数$K > 1$,即正反应发生更加完全时,正反应能够自发进行
- 平衡常数$K < 1$,即逆反应发生更加完全时,逆反应能够自发进行
9.1.13 自发发生,但是观察不到产物的原因
$$
\begin{aligned}
&\Delta G < 0 \\
&\downarrow \\
&自发进行 \\
&\downarrow \\
&但是活化能E_a极高 \\
&\downarrow \\
&反应难以发生, 反应速率极慢
\end{aligned}
$$
9.1.14 热化学常数只和温度有关!!!
第七章化学平衡当中的常数都是热化学常数!!!
热化学常数只和温度有关!!!
热化学常数只和温度有关!!!
热化学常数只和温度有关!!!
9.1.15 要把热化学常数和动力学的常数区分开!!!
第五章速率方程当中的常数是动力学常数!!!
第七章化学平衡当中的常数都是热化学常数!!!
虽然都是$k$, 但是一定要区分开!
9.2 溶解中的能量问题
9.2.1 网课期间有关溶解的知识点(国内体系)
9.2.1.1 溶解过程和溶解热现象
$$\ce {KMnO4 -> K+ + MnO4- (紫红色)}$$
- 溶液温度升高:$\ce {NaOH (s)、浓硫酸}$
- 溶液温度降低:$\ce {NH4NO3 (s)、NH4Cl (s)}$
- 溶液温度变化不大:$\ce {NaCl (s)}$
解释:
$$
溶解过程 \begin{cases}
扩散过程(物理过程) & 吸收热量 \\ 水合过程(化学过程) & 放出热量
\end{cases}
$$
比如:$\ce {Cu2+}$和水发生水合过程,生成水合铜离子,显蓝色
- $扩散过程中吸收的热量 > 水合过程中放出的热量 \rightarrow 溶液温度下降$
- $扩散过程中吸收的热量 < 水合过程中放出的热量 \rightarrow 溶液温度升高$
$$
溶液中的微粒
\begin{cases}
溶剂分子 \\ 溶质分子 / 离子 \\ 水合溶质分子 / 离子
\end{cases}
$$
$$\ce {HCl + H2O -> H3O+ + Cl-}$$
9.2.1.2 溶解和结晶
- 溶解:固体溶质扩散到溶剂中去的过程
- 结晶:固体溶质从溶液中析出的过程
$$\ce {固体物质 <=>[溶解][结晶] 溶液中的溶质}$$
- $v_{溶解} > v_{结晶}$,固体溶解(减少),不饱和溶液
- $v_{溶解} < v_{结晶}$,固体析出(增加),饱和溶液
- $v_{溶解} = v_{结晶}$,溶解平衡,饱和溶液
9.2.1.3 结晶水合物
- 晶体:自发形成的具有规则的几何形状的固体
- 结晶水合物:含有结晶水的固体
$$\ce {CuSO4*5H2O: 胆矾、蓝矾、硫酸铜晶体}$$
$$\ce {FeSO4*7H2O: 绿矾}$$
$$\ce {KAl(SO4)2*12H2O: 明矾}$$
$$\ce {CaSO4*2H2O: 生石膏}$$
$$\ce {2CaSO4*H2O: 熟石膏}$$
$$\ce {Na2CO3*10H2O: 石碱}$$
$$\ce {Na2SO4*10H2O: 芒硝}$$
- 风化:室温下干燥空气中失去部分或全部结晶水的现象
- 潮解:吸收空气中的水蒸气在固体表面形成溶液的现象
- 例如氢氧化钠作为干燥剂
9.2.2 离子晶体在水当中的溶解过程
Step 1:断离子键
因为$(s) \rightarrow (aq)$,所以:
$$
\Delta H > 0, \Delta S > 0
$$
Step 2:拉开溶剂分子
水的分子也拉开了,所以无序程度也增加了:
$$
\Delta H > 0, \Delta S > 0
$$
Step 3:形成新的稳定的吸引力
更加稳定了:
$$
\Delta H < 0, \Delta S < 0
$$
整个过程中的能量总结:
| Step | $\Delta S$ | $\Delta H$ | 能量的形式 |
|---|---|---|---|
| 1 | $+$ | $+$ | 晶格能 |
| 2 | $+$ | $+$ | 溶剂分子之间的能量 |
| 3 | $-$ | $-$ | 稳定的分子和离子间作用力 Ionic Dipole Force |
Unit 7 化学平衡 - Equilibrium
7.1 平衡常数 - Equilibrium Constant
7.1.1 浓度书写的平衡常数
对于可逆反应(Reversible Reaction):
$$
\ce {aA + bB <=> cC + dD}
$$
平衡常数:达到化学平衡时的
$$
K_{eq} = \frac {[\text C] ^ c [\text D] ^ d} {[\text A] ^ a [\text B] ^ b}
$$
固体(l)和液体(s)在这里算作是纯净的东西,不写进平衡常数。所以写在平很常数里的只有溶液(aq)和气体(g)
7.1.2 气体书写的平衡常数
对于只有气体的可逆反应,平衡常数还可以用气体的压强书写:
$$
K_p = \frac {\ce{P(C)}^c \ce{P(D)}^d} {\ce{P(A)}^a \ce{P(B)}^b}
$$
7.1.3 气体平衡常数与浓度平衡常数的关系
$$
K_p = K_c (RT) ^ {\Delta n}
$$
- 其中,$\Delta n$是反应式中生成物的系数总和减去反应物的系数综合。
原理:
$$
pV = nRT
$$
7.1.4 平衡常数的几个重要规律
1. 正逆反应的平衡常数互为倒数
2. 反应式相加,平衡常数相乘
3. 反应式系数翻倍,平衡常数平方
7.1.5 平衡常数的意义
- $K > 1$: 正反应进行得更加彻底
- $K < 1$: 逆反应进行得比较彻底
7.2 反应商 - Reaction Quotient
7.2.1 反应商 - Reaction Quotient
反应商是针对某个时刻的,不一定非要平衡状态,写法和平衡常数一样:
$$
Q = \frac {[\text C] ^ c [\text D] ^ d} {[\text A] ^ a [\text B] ^ b}
$$
7.2.1 反应商的应用 - 确定反应方向
- $K = Q$,平衡
- $K < Q$,逆反应方向, the reaction will proceed to the left, towards reactants
- $K = Q$,正反应方向, the reaction will proceed to the right, towards products
7.3 勒夏特列原理 - Le Chatelier's Principle
注:节7.3.1与节7.3.2摘自网课期间市教委网课笔记。
7.3.1 勒夏特列原理
勒夏特列原理(又称平衡移动原理): 如果改变影响平衡的个条件(如浓度、温度或压强等),平衡就向能够减弱这种改变的方向移动。
- 条件改变,平衡移动只是减弱外界条件带来的变化而不能完全抵消外界条件的变化。
- 从平衡移动的结果看,外界因素变化对平衡的影响占主导地位
- 勒夏特列原理既指明了条件改变,化学平衡移动的方向,也指明了化学平衡移动的结果。
7.3.2 勒夏特列原理的适用范围
- 适用于已达平衡的体系,不适用于未达平衡的体系。
- 适用于浓度、温度、压强等因素改变导致化学平衡发生移动的问题
- 不能用来判断新平衡建立所需要的时间
- 不仅适用于化学平衡,也适用于溶解平衡等其他动态平衡
7.3.3 勒夏特列原理的失效
对于反应:
$$
\ce {CaCO3 (s) <=> CaO (s) + CO2 (g)}
$$
在达到平衡之后如果充入二氧化碳,根据勒夏特列原理,最终压强将变大,然而,这是错误的。在这里,我们只看$K_p = p(\ce{CO2})$。所以,最终压强不变。
7.3.4 判断平衡常数的变化
- 如果反应朝正向移动,平衡常数变大
- 如果反应超逆向移动,平衡常数变小
7.4 溶解平衡 - Solubility Equilibrium
7.4.1 溶度积 $K_{sp}$ - Solubility Product
Ksp是对于难溶性离子化合物而言的,而且描述的是饱和状态时。
溶度积是指难溶电解质尽管难溶,但还是有一部分阴阳离子进入溶液,同时进入溶液的阴阳离子又会在固体表面沉积下来,当这两个过程的速率相等时,难溶电解质的溶解就达到平衡状态,固体的量不再减少。这样的平衡状态叫溶解平衡,其平衡常数叫溶度积常数(即沉淀平衡常数),简称溶度积(英语:solubility product)。
举个例子:
$$
\ce{Mg(OH)2 (s) <=> Mg2+ (aq) + 2OH- (aq)}
$$
$$
K_{sp} = [\ce{Mg2+}][\ce{OH-}]^2
$$
这里没有将氢氧化镁写在分母上,是因为它是固体,不写在平衡常数里面。
7.4.2 $K_{sp}$的一道重要例题
7.4.3 应用$K_{sp}$判断沉淀
- $Q > K_{sp}$:沉淀,precipitate
- $Q = K_{sp}$: 正好饱和,saturated
- $Q < K_{sp}$: 不沉淀
7.4.4 同离子效应 - Effect of a Common Ion on Solubility
就是对溶解平衡应用勒夏特列。
比如说:
$$
\ce{Mg(OH)2 (s) <=> Mg2+ (aq) + 2OH- (aq)}
$$
根据勒夏特列,更多的$\ce{OH-}$会将反应朝逆向移动。$\ce{OH-}$的浓度将增加,$\ce{Mg2+}$的浓度将下降。
7.4.5 生成沉淀的顺序
首先生成更难溶的沉淀
Unit 8 酸碱理论 - Acid and Bases
8.1 酸碱理论 - Acid and Bases
8.1.1 水的离子积与pH值
8.1.1.1 水的离子积 - Ion Product Constant for Water
水会微弱地电离
$$
\ce {H2O(l) <=> H+(aq) + OH-(aq)}
$$
在$298K$时,
$$
K_w = \ce {[H+][OH-]} = 1 \times 10 ^ {-14}
$$
8.1.1.2 水的电离程度的变化
越热越电离,越稀越电离
8.1.1.3 pH值
$$
\ce {pH} = - \lg \ce {[H+]}
$$
8.1.1.4 pH值与酸碱性的关系
- 在$298K$的时,pH=7时溶液呈中性
- 高于$298K$时,pH=7时溶液呈碱性
- 低于$298K$时,pH=7时溶液呈酸性
8.1.1.5 pOH值
$$
\ce {pOH} = - \lg \ce {[OH-]}
$$
8.1.2 酸碱的定义
8.1.2.1 电离酸碱理论 - Arrhenius
- 在水溶液中电离出$\ce {H+}$的是酸
- 在水溶液中电离出$\ce {OH-}$的是碱
8.1.2.2 路易斯酸碱理论 - Lewis
- 酸在溶液中是电子对的接收者,acceptors
- 碱在溶液中是电子对的提供者,donors
8.1.2.3 质子酸碱理论 - Bronsted-Lowry
- 酸是质子的提供者,proton donors
- 碱是质子的接收者,proton acceptors
8.1.3 两性物质 - Amphorteric Chemicals
既可以得到质子,又可以失去质子的物质
$$
\ce {HCO3- (aq) + H+ (aq) -> H2CO3 (aq)}
$$
$$
\ce {HCO3- (aq) + OH- (aq) -> CO3^2- (aq) + H2O (l) }
$$
8.1.4 强酸强碱 - Strong Acids & Bases
8.1.4.0 什么是强酸强碱
在水中能够完全电离出氢离子或氢氧根
8.1.4.1 强酸 - Strong Acids
| 化学式 | 英文 |
|---|---|
| $\ce {HCl} $ | Hydrochloric Acid |
| $\ce {HBr} $ | Hydrobromic Acid |
| $\ce {HI} $ | Hydroiodic Acid |
| $\ce {HNO3} $ | Nitric Acid |
| $\ce {H2SO4} $ | Sulfuric Acid |
| $\ce {HClO4} $ | PerCloric Acid |
8.1.4.2 强碱 - Strong Bases
第一主族的碱金属形成的碱。以及$\ce {Sr(OH)2}$, $\ce {Ba(OH)2}$
8.1.5 弱酸弱碱 - Weak Acids & Bases
8.1.5.1 什么是弱酸弱碱
在水中部分电离
8.1.5.2 $K_a$ - Acid Ionization Constant
对于
$$
\ce {HX (aq) <=> H+ (aq) + X- (aq)}
$$
$$
K_a = \frac {\ce {[H+][X-]}} {\ce {[HX]}}
$$
8.1.5.3 $K_b$ - Base Ionization Constant
对于
$$
\ce {B (aq) + H2O <=> OH- (aq) + HB+ (aq)}
$$
$$
K_b = \frac {\ce {[OH-][HB+]}} {\ce {[B]}}
$$
8.1.5.4 通过$K_a$, $K_b$计算pH值
$$
K_a = \frac {\ce {[H+][X-]}} {\ce {[HX]}} = \frac {\ce {[H+]}^2} {\ce {[HX]}}
$$
$$
\Rightarrow \ce {[H+]} = \sqrt {K_a{\ce {[HX]}}}
$$
$$
\ce {pH} = -\lg \ce {[H+]} = -\lg \sqrt {K_a{\ce {[HX]}}} \approx -\lg \sqrt {K_a{\ce {c(HX)}}}
$$
8.1.6 盐 - Salt
8.1.6.1 盐的酸碱性
- 强酸强碱盐 - 中性
- 强酸弱碱盐 - 酸性
- 强碱弱酸盐 - 碱性
8.1.6.2 水解 - Hydrolysis
举例:
$$
\ce {Fe^3+ + 6H2O <=> Fe(OH)3 + 3H3O+}
$$
$$
\ce {CH3CH2COO- + H2O <=> CH3CH2COOH + OH-}
$$
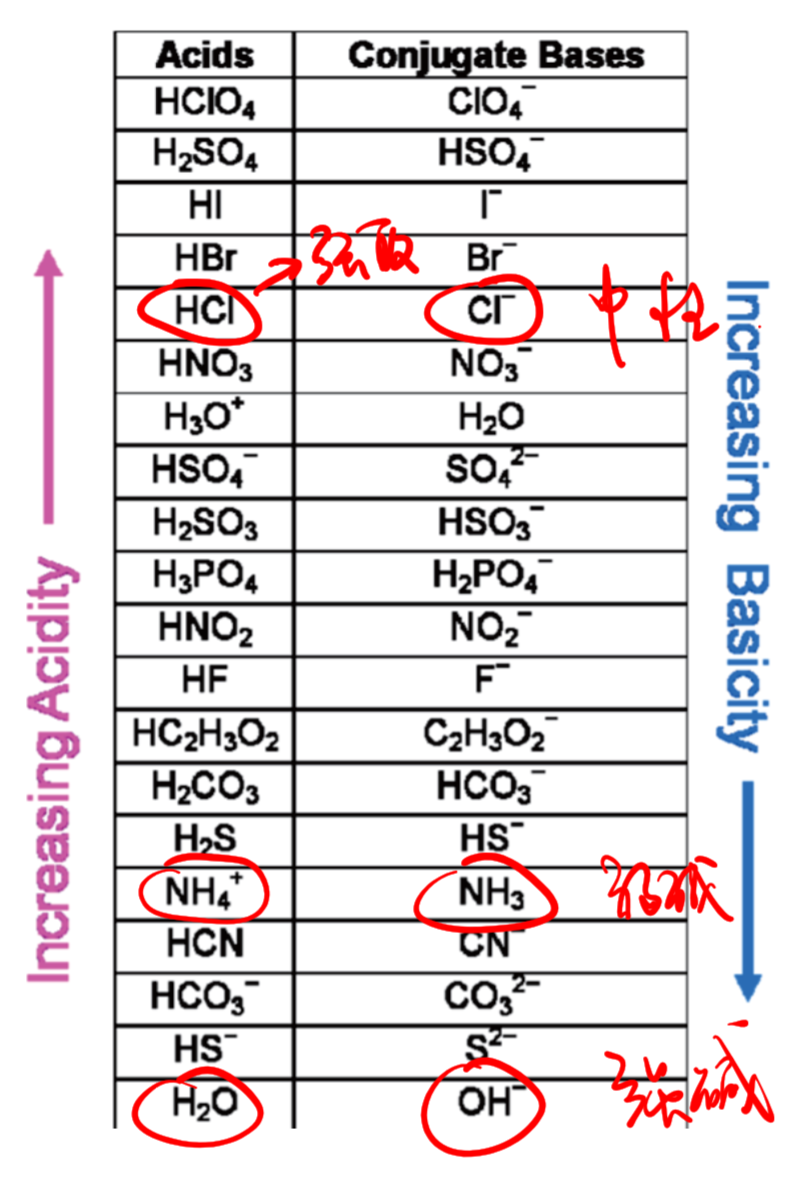
8.1.7 共轭酸碱对 - Conjugate Acid Base Pair
8.1.7.1 什么是共轭酸碱对?
质子理论阐述,能给出质子的分子或离子是酸,能接受质子的分子或离子是碱,酸给出质子转变为相应的碱,碱接受质子转变为相应的酸,这种因质子得失而相互转变的一对酸碱称为共轭酸碱对。
举例:
$$
\ce {HX + H2O <=> X- + H3O+}
$$
- $\ce {HX}$是酸,失去了质子,形成了它的共轭碱$\ce {X-}$
- $\ce {H2O}$是碱,得到了质子,形成了它的共轭酸$\ce {H3O+}$
8.1.7.2 如何判断共轭酸碱对?
共轭酸比共轭碱多一个$\ce {H+}$(质子)
8.1.7.3 共轭酸碱对的重要的三句话
- 酸性越强,共轭碱的酸性越弱
- 碱性越强,共轭酸的碱性越弱
- 弱酸对应的共轭碱一般也是弱碱(注意相对的概念)
8.1.7.4 共轭酸碱对的$K_a \times K_b = K_w$
共轭酸的电离程度$K_a$和其对应的共轭碱的电离程度$K_b$的乘积是$K_w$
用醋酸的举例来进行证明:
$$
\ce {CH3COOH (aq) + H2O(l) <=> CH3COO- (aq) + H3O+ (aq)}
$$
$$
K_a = \frac {\ce {[CH3COO-][H3O+]}} {\ce {[CH3COOH]}} = \frac {\ce {[CH3COO-][H+]}} {\ce {[CH3COOH]}}
$$
共轭碱的电离:
$$
\ce {CH3COO- (aq) + H2O (l) <=> CH3COOH (aq) + OH- (aq)}
$$
$$
K_b = \frac {\ce {[CH3COOH][OH-]}} {\ce {[CH3COO-]}}
$$
所以
$$
K_a \times K_b = \ce {[H+][OH-]} = K_w
$$
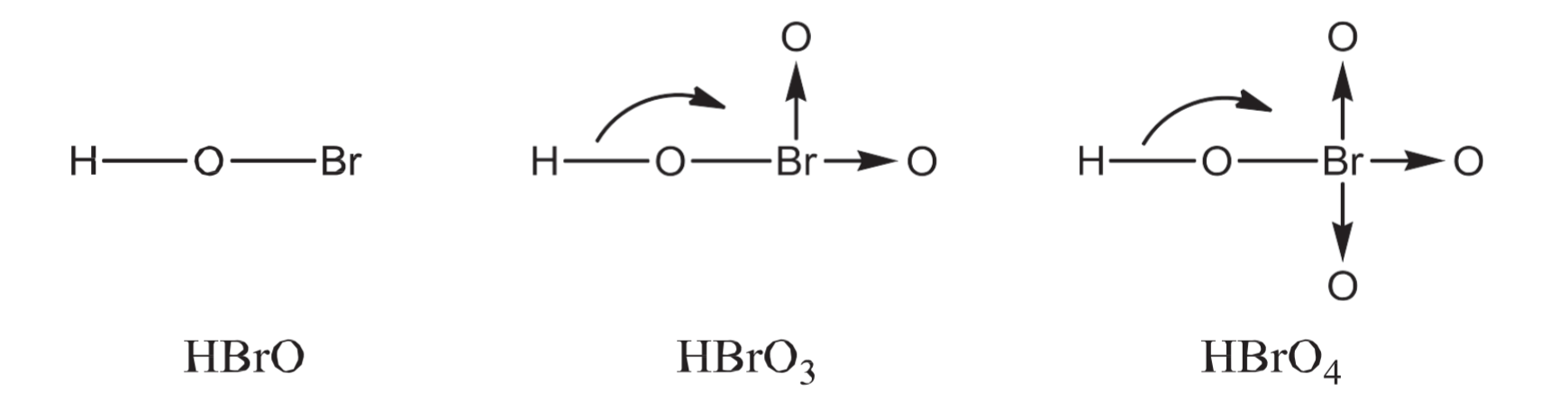
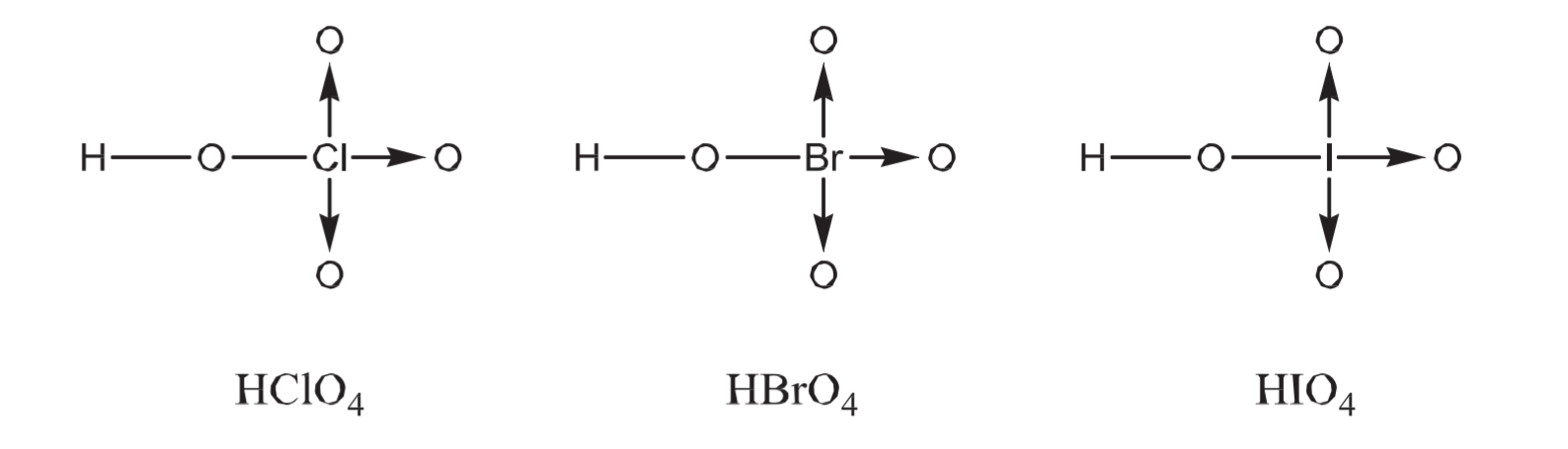
8.1.8 含氧酸的酸性比较 - Acid Length of Oxoacids
8.1.8.1 中心原子相同的情况
$$
\begin{aligned}
&氧原子数量\uparrow (\text{More Oxygen Atoms}) \\
&\downarrow \\
&\text {Lower }\ce {H-O}\text { Bond / Electron Density} \\
&\downarrow \\
&\text {More easily }\ce {H+}\text { Lost} \\
&\downarrow \\
&\text {Stronger Acid}
\end{aligned}
$$
8.1.8.2 氧原子数量相同的情况
$$
\begin{aligned}
&电负性\uparrow (\text{Greater Electronegativity}) \\
&\downarrow \\
&\text {Lower }\ce {H-O}\text { Bond / Electron Density} \\
&\downarrow \\
&\text {More easily }\ce {H+}\text { Lost} \\
&\downarrow \\
&\text {Stronger Acid}
\end{aligned}
$$
8.1.9 酐 - Anhydride
8.1.9.1 酸酐 - Acid Anhydride
酸酐与水反应生成酸:
$$
\ce {SO2 + H2O -> H2SO3}
$$
8.1.9.2 碱酐 - Base Anhydride
其实就是金属氧化物,与水反应生成碱:
$$
\ce {Na2O + H2O -> 2NaOH}
$$
8.2 缓冲溶液 - Buffer Solution
8.2.1 缓冲溶液的作用
向缓冲溶液中加入一定量的酸或碱,可以减弱pH值得改变
8.2.2 缓冲溶液的组成
一定是弱酸与共轭碱,或弱碱与共轭酸
8.2.3 缓冲溶液的原理
拿醋酸和醋酸根组成的缓冲溶液举例,
$$
\ce {CH3COOH + OH- -> CH3COO- + H2O}
$$
$$
\ce {CH3COO- + H+ -> CH3COOH}
$$
8.2.4 缓冲溶液的两种制备方法
- 直接配置
- 通过反应配得:
- 过量弱酸 + 少量强碱
- 过量弱碱 + 少量强酸
8.2.5 缓冲溶液pH值 - Henderson-Hasselbalch Equation
$$
\ce {pH = pK_a} + \lg \frac {\ce {[A-]}} {\ce {[HA]}}
$$
$$
\ce {pOH = pK_b} + \lg \frac {\ce {[HB+]}} {\ce {[B]}}
$$
推导:
$$
\ce {HA <=> H+ + A-}
$$
$$
K_a = \frac {\ce {[H+][A-]}} {\ce {[HA]}}
$$
碱类似。
8.2.6 最有效的缓冲溶液
当$\ce {[A-] = [HA]}$时,缓冲溶液最有效(most effective),因为既能中和酸,也能中和碱。
此时:
$$
\ce {pH = pK_a}
$$
8.3 滴定 - Titration
8.3.0 标准液的术语
Standard Solution / Titrant
8.3.1 中和点/等当量点 - Equivalence Point
恰好反应的点
8.3.2 滴定终点 - Endpoint
看到指示剂变色的点
8.3.3 滴定求浓度
原理:
$$c_1V_1 = c_2V_2$$
8.3.4 滴定判断酸碱的强弱
- 强酸强碱滴定,等当量点pH值等于7,因为生成强酸强碱盐
- 强酸滴定弱碱,等当量点pH值小于7,因为生成强酸弱碱盐
- 强碱滴定弱酸,等当量点pH值大于7,因为生成强碱弱酸盐
8.3.5 不同酸碱滴定终点的pH比较
- 待滴定的酸,酸性越弱,$K_a$值越低,生成的共轭碱碱性越强,$K_b$值越大,等当量点pH值越高
- 待滴定的碱,碱性越弱,$K_b$值越低,生成的共轭酸酸性越强,$K_a$值越大,等当量点pH值越低
8.3.6 半等当量点/半中和点 - Half Equivalence Point
半等当量点时,弱酸被反应了一半,此时溶液中:
$$
\ce {[HA] = [A-]}
$$
此时
$$
\ce {pH = pK_a}
$$
8.3.7 滴定求$\ce {p K_a}$值
半等当量点的pH值时pKa值
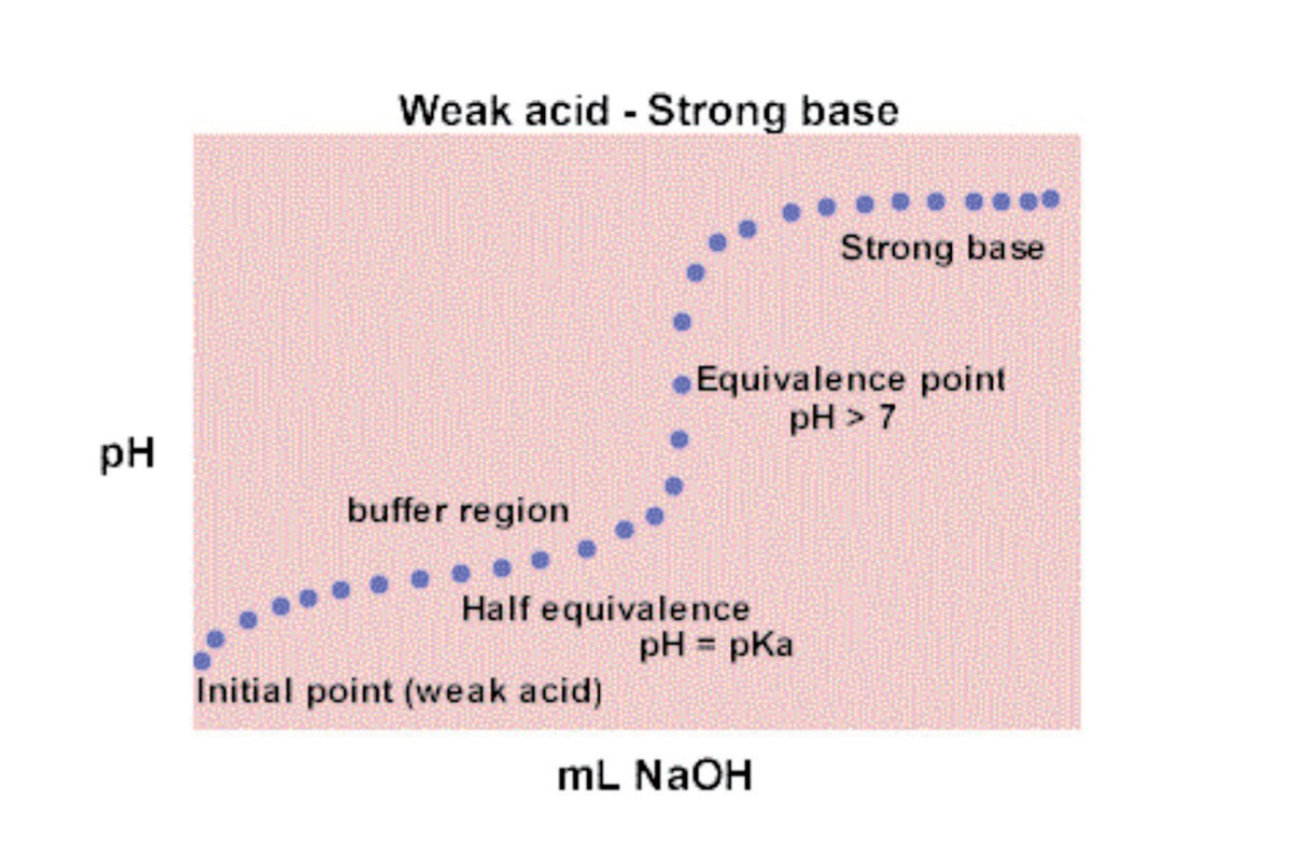
8.3.8 滴定图像的分析
拿弱酸举例:
- Initial:Weak Acid
- Before Half Equivalence: $\ce{[HA] > [A-]}$
- At Half Equivalence: $\ce {[HA] = [A-]}$
- After Half Equivalence: $\ce {[HA] = [A-]}$
- At Equivalence: $\ce {HA -> A-}$
- After Equivalence: Base
在Equivalence之前是Buffer Region
8.3.9 常用的酸碱指示剂
- Phenolphthalein 酚酞
- Litmus 石蕊
8.3.10 滴定指示剂的选取
指示剂在 Equivalence Point 的时候变色
8.3.11 滴定指示剂的变色范围
举例:
$$
\begin{aligned}
&\ce {H-Indicator (aq)} & \ce { <=> H+ (aq) + Indicator-} & \ce { (aq)} \\
&\ce {Red} & \ce {Yellow} &
\end{aligned}
$$
- $\ce {pH = pK_a}$时,$\ce {[HIn] = [In-]}$,显叠加颜色
- $\ce {pH < pK_a}$时,$\ce {[HIn] > [In-]}$,显$\ce {HIn}$颜色(红色)
- $\ce {pH > pK_a}$时,$\ce {[HIn] < [In-]}$,显$\ce {In-}$颜色(黄色)
解释方法(1):同离子效应,更多的氢离子,pH降低,平衡朝左侧移动,基本上都是弱酸
解释方法(2):
$$
\ce {pK_a = pH } + \lg \frac {\ce {[In-]}} {\ce {[HIn]}}
$$
8.3.12 滴定指示剂的人眼变色范围
$$
\ce {pK_a - 1\leq pH \leq pK_a + 1}
$$
- 当$\displaystyle \frac {\ce {[HIn]}} {\ce {[In-]}} \geq 10$, 显$\ce {HIn}$颜色
- 当$\displaystyle \frac {\ce {[HIn]}} {\ce {[In-]}} \leq \frac 1 10$, 显$\ce {In-}$颜色
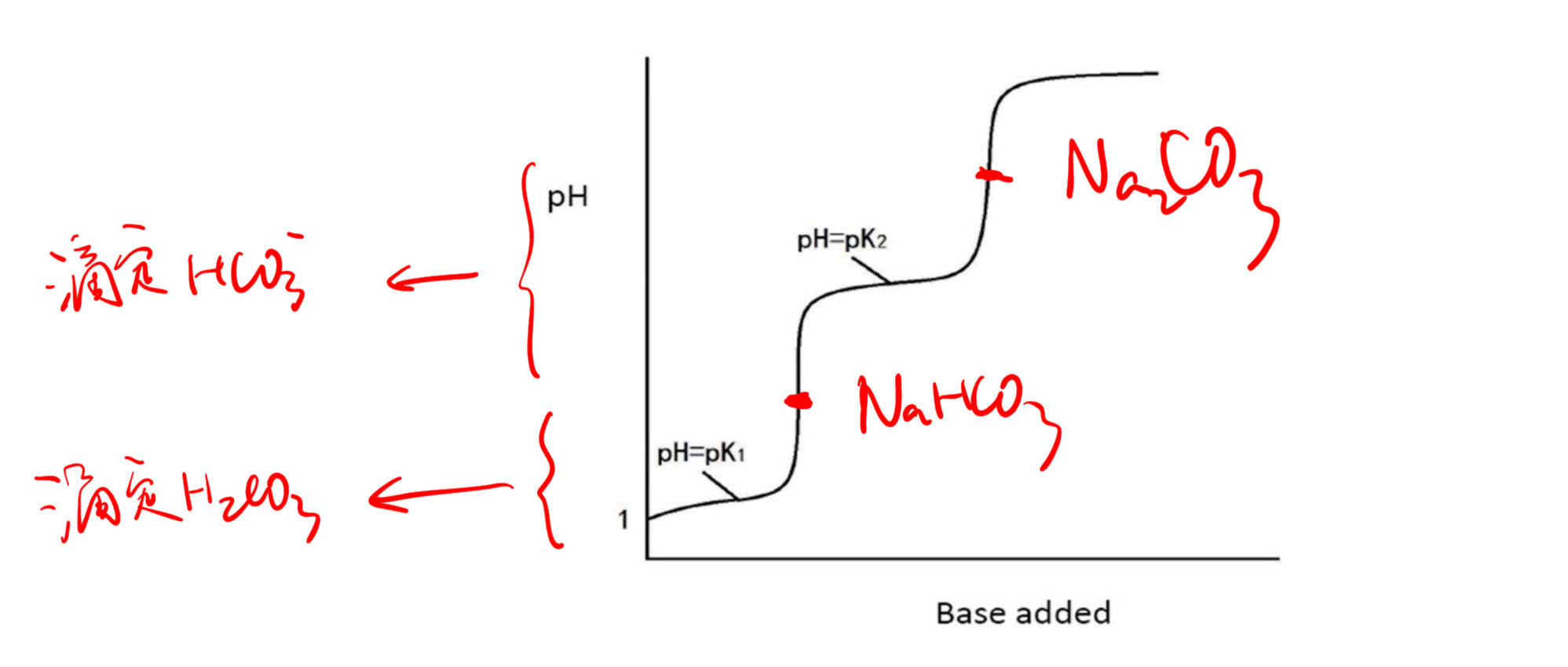
8.3.13 多元酸的滴定图像 - Polyatomic Acid-Base Titration
Unit 9 热化学的应用 - Applications of Thermodynamics
9.3 电化学 - Electrochemistry
9.3.1 原电池 - Voltaic Cell
9.3.1.1 原电池 - Voltaic Cell
通过氧化还原反应而产生电流的装置称为原电池,也可以说是将化学能转变成电能的装置。有的原电池可以构成可逆电池,有的原电池则不属于可逆电池。原电池放电时,负极发生氧化反应,正极发生还原反应。例如铜锌原电池又称丹尼尔电池,其正极是铜极,浸在硫酸铜溶液中;负极是锌板,浸在硫酸锌溶液中。两种电解质溶液用盐桥连接,两极用导线相连就组成原电池。平时使用的干电池,是根据原电池原理制成的。
原电池、电解池都以发生在电子导体(如金属)与离子导体(如电解质溶液)接触界面上的氧化还原反应为基础。
Voltaic Cell, Galvanic Cell 都是原电池
9.3.1.2 原电池阴阳极发生的半反应
$$
\ce {Zn -> Zn^2+ + 2e-}
$$
$$
\ce {Cu^2+ + 2e- -> Cu}
$$
- Anode 阳极,Oxidation 氧化
- Cathode 阴极,Reduction 还原
注意:这里只写$\ce {+e-}$,不写减号。
9.3.1.3 盐桥 - Salt Bridge
- 反应掉了阳离子,就补充阳离子
- 生成了阳离子,就补充阴离子
9.3.1.4 金属活动性顺序
$$
\ce {K, Ca, Na, Mg, Al, Zn, Fe, Sn, Pb, H, Cu, Hg, Ag, Pt, Au}
$$
- 越往右,金属的失电子能力越弱
- 越往右,金属阳离子的得电子能力越强
9.3.1.5 标准电极电势 $E^\circ$
写在前面:这里用${}^\circ$表示标准状态(类似于熵、焓、吉布斯自由能)。
- 还原电势:描述物质得电子的趋势 (tendency)
- 氧化电势:描述物质失电子的趋势 (tendency)
- 规定:$\ce H$的氧化电势和还原电势都是0V
- 氧化电势和还原电势互为相反数
$$
E^\circ_{\text{Oxidation}} = -E^\circ_{\text{Reduction}}
$$
9.3.1.6 反应式中的 $E^\circ$
对于反应中最后的$E^\circ$:
- 如果是氧化反应,那么$E^\circ$代表氧化电势
- 如果是还原反应,那么$E^\circ$代表还原电势
举例:
$$
\ce {Zn -> Zn^2+ + 2e-, E^\circ = 0.76V}
$$
$$
\ce {Zn^2+ + 2e- -> Zn, E^\circ = -0.76V}
$$
第一个反应是氧化反应,$E^\circ$代表氧化电势。第二个反应是还原反应,$E^\circ$代表还原电势。
9.3.1.7 $E^\circ$描述电势差
不管$E^\circ$是氧化电势还是还原电势,他们都描述的是生成物到反应物的电势差,即:
- 如果反应的$E^\circ > 0$,这个反应物到生成物,电势增加
- 如果反应的$E^\circ < 0$,这个反应物到生成物,电势降低
举例:
$$
\ce {Zn -> Zn^2+ + 2e-, E^\circ = 0.76V}
$$
从锌板到溶液中的锌离子,电势升高了$\ce {0.76V}$。而锌在原电池中是阳极,也就是负极,从负极到正极电势增加,和结论相符。
9.3.1.8 多个反应式相加$E^\circ$不需要乘系数
两个半反应拼成一个反应时,不需要管系数,直接将$E^\circ$相加!!
两个半反应拼成一个反应时,不需要管系数,直接将$E^\circ$相加!!
两个半反应拼成一个反应时,不需要管系数,直接将$E^\circ$相加!!
这不是很难理解,因为$E^\circ$没描述的是物质的趋势/能力,和量是没关系
9.3.1.9 通过$E^\circ$判断原电池反应能否发生
当总反应式$\sum E^\circ > 0$时,这个氧化还原反应可以自发进行
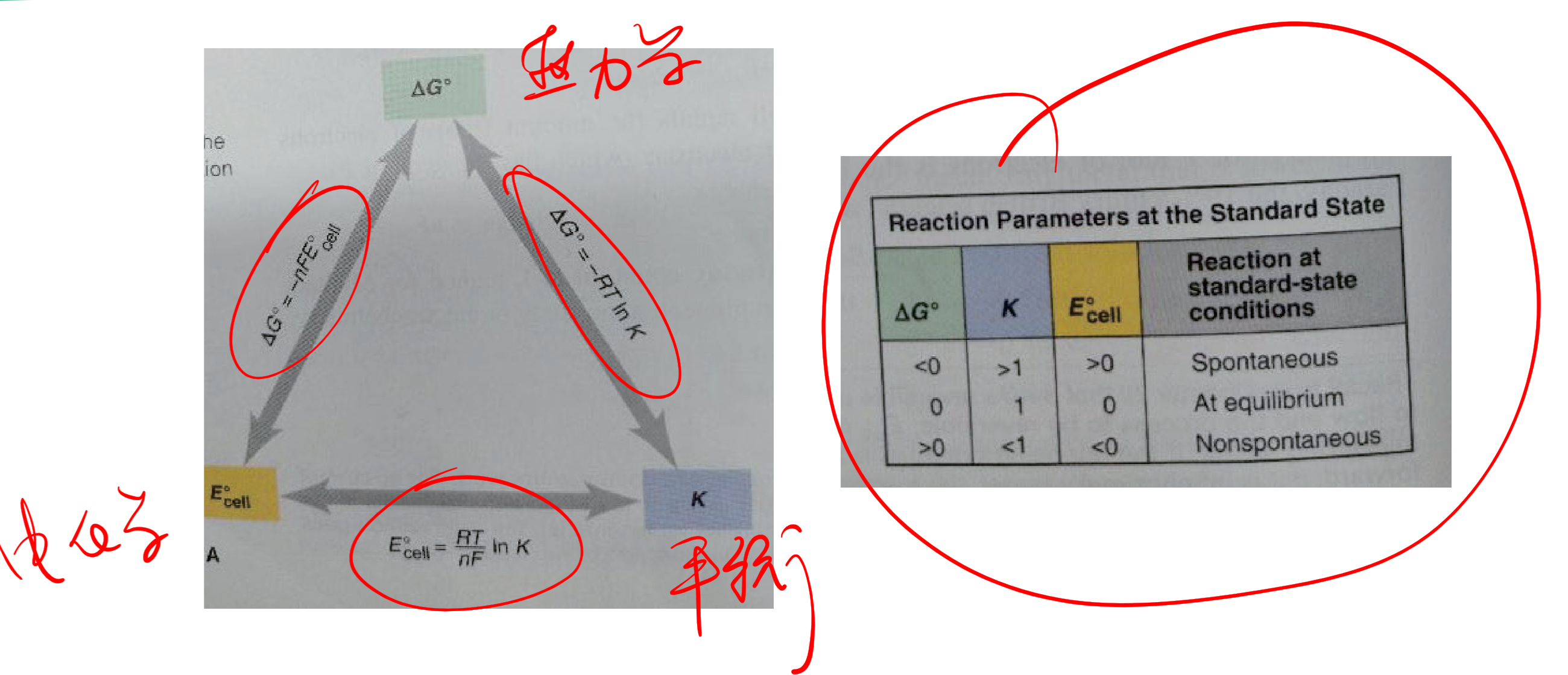
9.3.1.10 能斯特方程 - 非标准状态的$E$ - Nernst Equation
$$
E = E^\circ - \frac {RT} {nF} \ln Q
$$
- $Q$是反应商
- $RT$是$pv=nRT$里的RT
- $n$是转移的电子数
- $F$是法拉第常数
9.3.1.11 什么是转移的电子数
其实这个理解起来并不是很困难,在解体时直接就按照题目给出的方程式来写,最后单位后加上$/\text{mol}_\text{rnx}$
9.3.1.12 非标准状态的$E$的变化的讨论
标准状态下的浓度为$1 \text{mol/L}$,所以标准状态下的反应商为:
$$
Q = \frac {1 ^ c \times 1 ^ d} {1 ^ a \times 1 ^ b} = 1
$$
此时:
$$E = E^\circ - \frac {RT} {nF} \ln 1 = E^\circ$$
在非标准状态下,我们主要讨论反应商对$E$的影响:
- 反应商$Q \uparrow (Q > 1)$,意味着更多的生成物(更少的反应物),根据公式,$E \downarrow$
- 反应商$Q \downarrow (Q < 1)$,意味着更少的生成物(更多的反应物),根据公式,$E \uparrow$
- 反应商$Q = 1$,就是$E^\circ$
9.3.1.13 $E$与$\Delta G$
$$
\Delta G ^ \circ = -nFE ^ \circ
$$
-
$\Delta G$: 吉布斯自由能的变化
-
$n$: 转移的电子数
-
$F$: 法拉第常数
-
$E$: reaction potential
-
$E > 0$, $\Delta G < 0$:自发发生
-
$E < 0$, $\Delta G > 0$: 不自发发生
9.3.1.14 电化学、热力学、与平衡的关系
9.3.2 电解池 - Electrolytic Cells
9.3.2.1 什么是电解池
电解池的主要应用用于工业制纯度高的金属,是将电能转化为化学能的一个装置(构成:外加电源,电解质溶液,阴阳电极)。使电流通过电解质溶液或熔融电解质而在阴,阳两极引起还原氧化反应的过程。
9.3.2.2 用$E$判断放电顺序
- 以阳极为例:阳极发生氧化反应,化合价升高,失电子。那么,在所有可以发生的氧化半反应当中,氧化电势最高的那个,最先发生。即,失电子能力最强。
- 以阴极为例:阴极发生还原反应,化合价降低,得电子。那么,在所有可以发生的还原半反应当中,还原电势最高的那个,最先发生。即,得电子能力最强
9.3.2.3 为什么有点放电顺序和上一节看起来矛盾?
对于某些物质,特别是$\ce{H2O}$, 会发生一些和上一届结论矛盾的现象。我们拿电解$\ce{CuCl2}$举例:
在阳极能够发生的两个氧化反应分别为:
$$
\ce {2Cl- -> Cl2 (l) + 2e-}
$$
$$
\ce {2H2O (l) -> O2 (g) + 4H+ + 4e-}
$$
第一个反应的还原电势为$1.358\text V$,第二个反应的还原电势为$1.229\text V$,所以第一个反应的氧化电势为$-1.358\text V$,第二个反应的氧化电势为$-1.229\text V$,第二个更高,理论上更先发生。然而,实验证明先出氯气。
所以,对于水或其他一些物质,可能会有超电势的现象
9.3.2.4 超电势
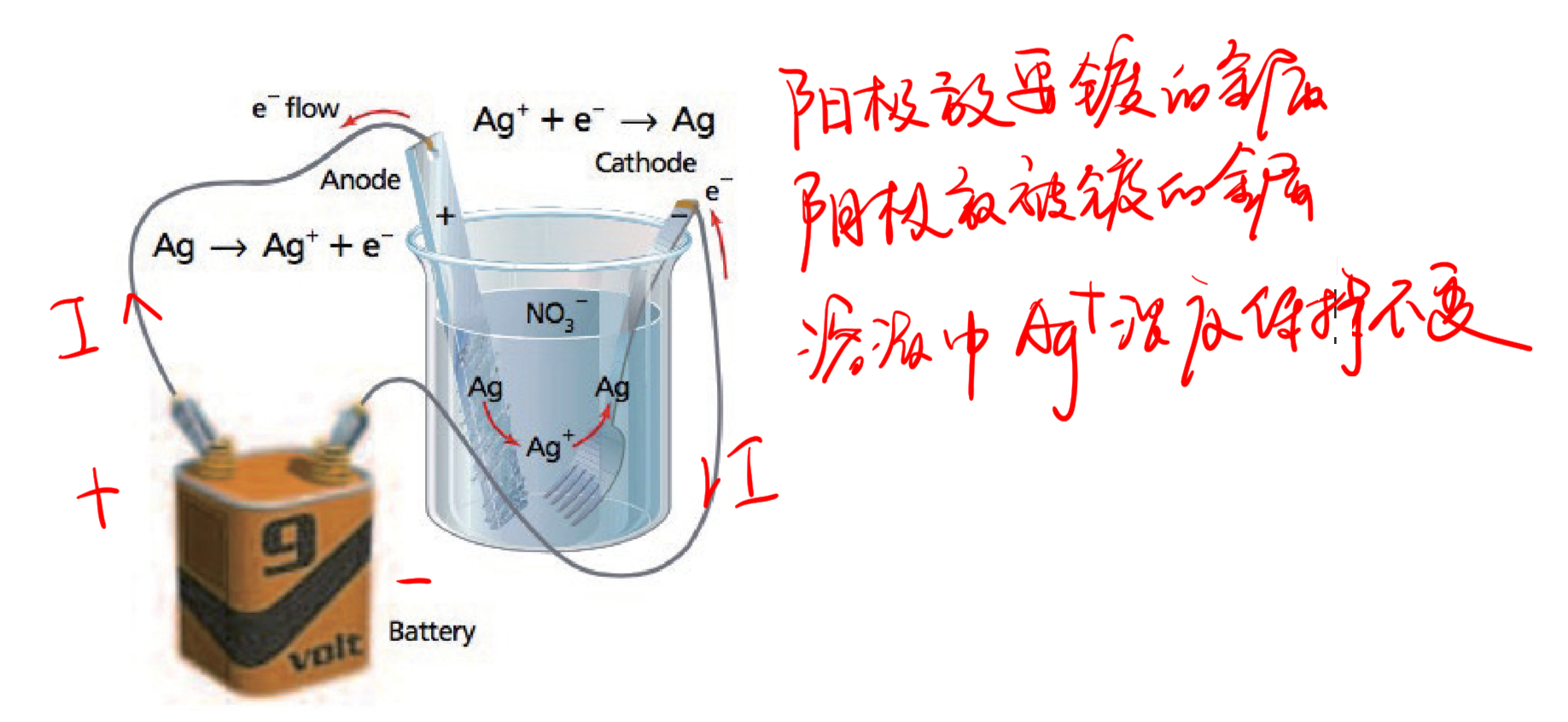
9.3.2.5 电解池的应用 - 电镀
- 阳极放要镀的金属
- 阴极放被镀的金属
- 溶液中金属离子浓度几乎保持不变
9.3.3 电解池与原电池的比较
| 电解池 | 原电池 | |
|---|---|---|
| 能量转换 | $化学能 \rightarrow 电能$ | $电能 \rightarrow 化学能$ |
| 阳极 | 氧化 | 氧化 |
| 阴极 | 还原 | 还原 |
Appendix - 附录:补充知识
A.1 核反应 - Nuclear Chemistry
A.1.1 $\alpha$衰变 - Alpha Decay
放出$\ce{He}$核
A.1.2 $\beta$衰变 - Beta Decay
放出高速电子流
A.1.3 正$\beta$衰变 - Positive Beta Decay
放出正电子
A.1.4 $\gamma$衰变 - Gamma Decay
是$\alpha$, $\beta$衰变时同时产生的,不会单独发生
A.1.5 核反应的反应级数
衰变反应都是一级反应!!!!因为半衰期确定
$$
t_{1/2} = \frac {\ln 2} {k}
$$
A.1.6 重核裂变
链式反应:
$$
\ce {^235_292 U + ^1_0n -> ^87_35Br + ^146_57La + 3 ^1_0n} {}
$$
A.1.7 轻核聚变
$$
\ce {^2_1 H + ^3_1 H -> ^4_2 He + ^1_0n}
$$
A.2 有机化学
| 物质 | 名称 |
|---|---|
| 烷烃 | Alkane |
| 烯烃 | Alkene |
| 炔烃 | Alkyne |
| 甲烷 | Methane |
| 乙烷 | Ethane |
| 丙烷 | Propane |
| 丁烷 | Butane |
| 戊烷 | Pentane |
| 同分异构体 | isomer |
| 醇 | Alcohol |
| 羧基 | Carboxyl |
| 卤代烃 | Haloalkane |
| 氨基 | Amnies |
| 醛基 | Aldehyde |
| 酮 | Ketone |
| 醚 | Ether |
| 酯 | Ester |
| 酯脱水缩合 | Esterification |
| 卤化 | Halogenation |
| 加聚 | Polymerization |
| 裂解 | Cracking |
| 加成 | Addition |
| 发酵 | Fermentation |
A.3 实验 - Lab
A.3.1 乘除的有效数字
与参与运算的最少的有效数字位数保持一致
A.3.2 加减的有效数字
与参与运算的小数点后最小的数位保持一致
A.3.3 精度与准确度 - Precision & Accuracy
Precision --> 所有结果都互相很Close
Accuracy --> Correct
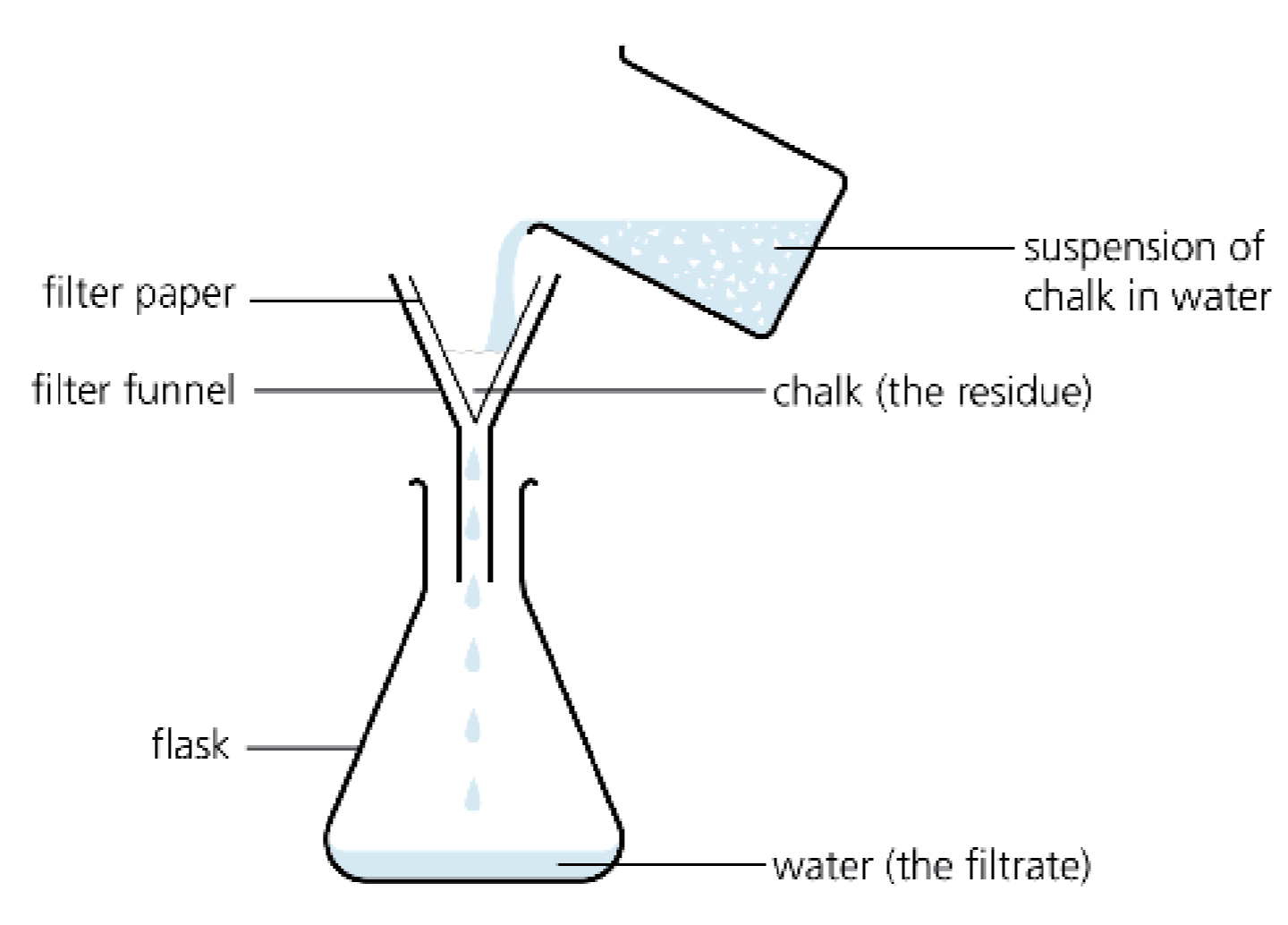
A.3.4 过滤 - Filtration
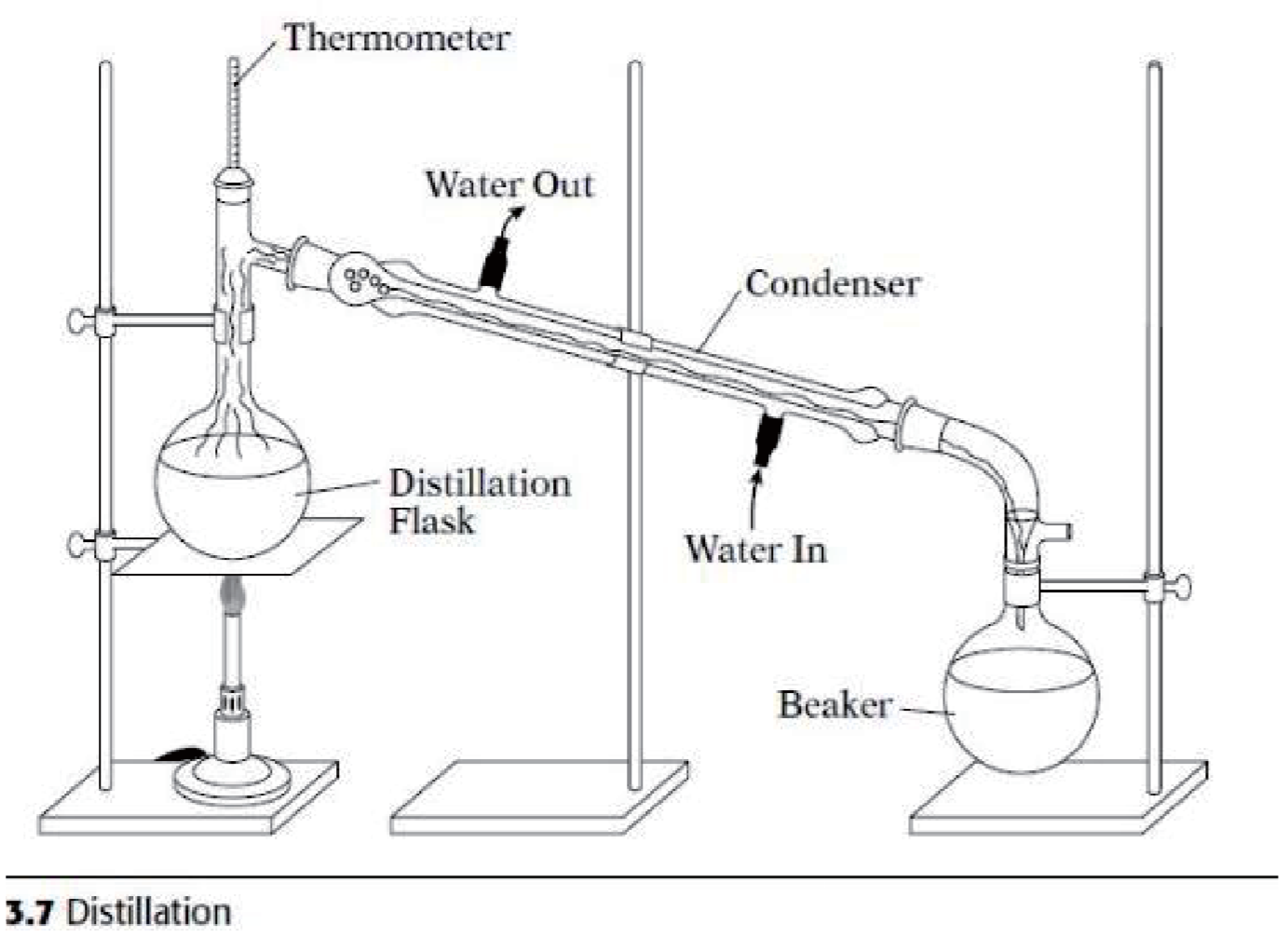
A.3.5 蒸馏 - Distillation
A.3.6 纸层析法 - Paper Chromatography
用溶解度为原理进行分离
A.3.7 柱层析法 - Column Chromatography
$$
\begin{aligned}
&待分离物 \\
&\downarrow \\
&放入柱形容器 \\
&\downarrow \\
&会被吸附住 \\
&\downarrow \\
&加洗脱液 \\
&\downarrow \\
&溶解度高就先流出
\end{aligned}
$$
A.3.8 排水法收集气体
注意:集满时,内部压强等于大气压,且需要注意水蒸气的分压,不如:
$$
p_{\text {atm}} = p_{\ce {O2}} + p_{\ce {H2O}}
$$
A.3.9 向上/下排空气法
A.3.10 分光光度法 - Spectrophotometry
根据Beer's Law测定浓度,因为;
$$
A = abc
$$
A.3.11 重量分析法 - Gravimetric Analysis
其实就是沉淀(precipitation),根据重量分析
A.3.12 滴定 - Titration
使用Buret(滴定管)、pipet(移液管)精确量液体。
零散的小点
关于计算
看FRQ的答案,式量貌似要小数点后两位,具体的按照考试的时候那张表上的。