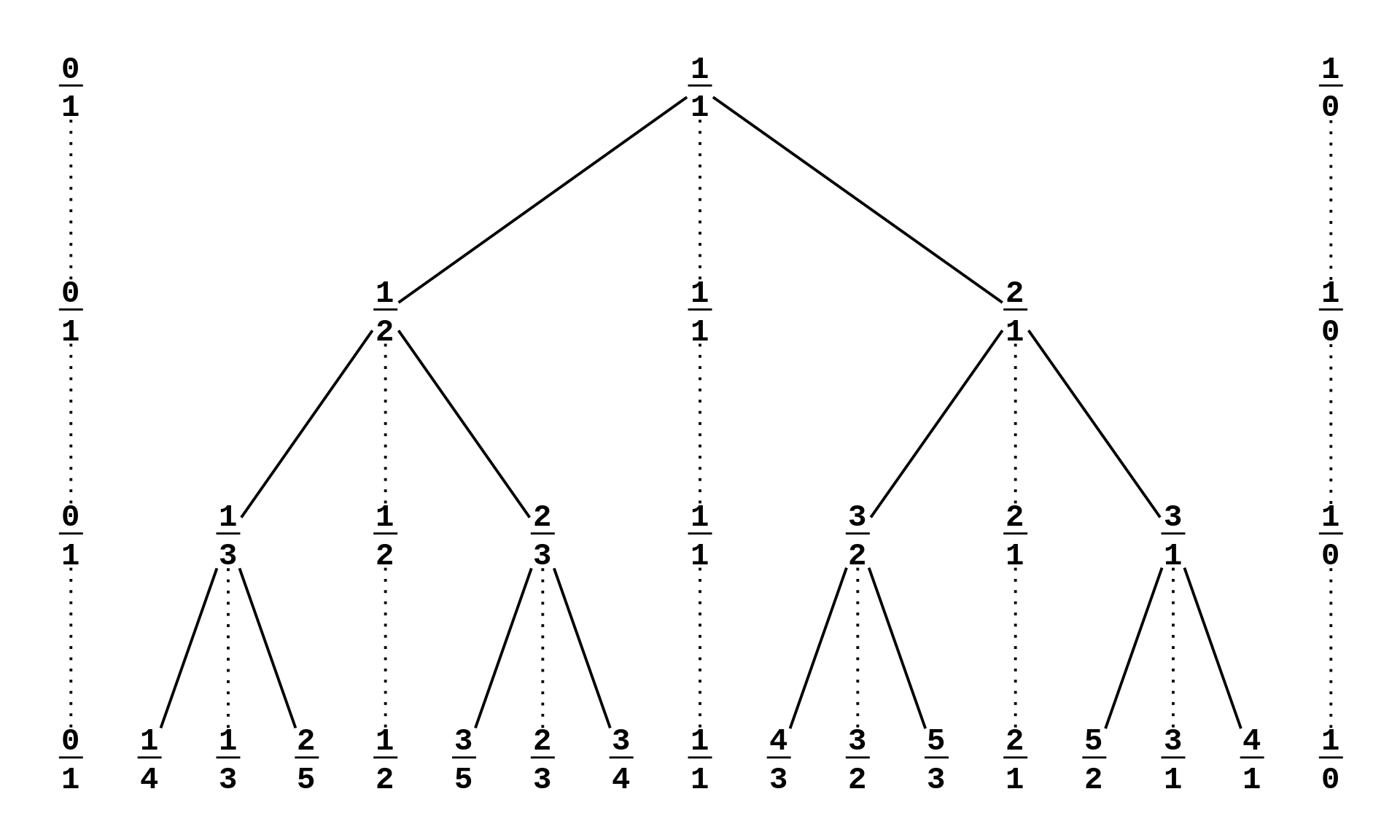
Stern-Brocot Tree
我们主要研究下面几个问题：
- 为何出现在这棵树中的每个数都是最简分数，即 $m\perp n$
- 为何所有可能的分数 $m/n$ 都恰好出现一次
- 为何所有的数从左到右都是递增的
介绍
参加具体数学 4.5 互素 Relative Primality
重要结论：$m'n-n'm=1$
证明：
我们首先验证初始情况：$1\times 1-0\times 0=1$，成立。
接下来我们考虑任意的 $m/n, m'/n'$。当插入新的中位分数 $(m+m')/(n+n')$ 时，我们所需要验证的条件就变为了：
$$
(m+m')n-m(n+n')=1
$$
$$
m'(n+n')-(m+m')n'=1
$$
可以发现，其等价于插入前的条件：
$$
m'n-n'm=1
$$
所以，每插入一个新的中位分数我们并不需要判断新的情况，反而只需要往上回溯，判断其插入前的条件。我们可以发现所有的数都可以回溯到最初的 $0/1$ 和 $1/0$。我们已经验证了这个情况的正确性，遂证明了这个结论。
中位分数必定是最简分数
接下来，我将要证明：若 $m'n-n'm=1$，则必然有 $\gcd(m'+m,n'+n)=1$.
由于我们有：
$$
m'n-n'm=1
$$
将其进行改写，不难得出：
$$
n(m+m')-m(n+n')=1
$$
也就是说，存在整数解 $(x,y) \in \mathbb Z^2$ 使得
$$
(m+m')x+(n+n')y=1
$$
有解 (取 $x=n, y=-m$)。根据裴蜀定理，我们就必然有
$$
\gcd(m+m',n+n') \mid 1
$$
所以
$$
\gcd(m+m',n+n') = 1
$$
递增性：$m/n < (m+m')/(n+n') < m'/n'$
若 $m/n < m'/n'$，则上式必然成立。因为不难证明：
$$
\frac m n - \frac {m+m'}{n+n'} < 0
$$
$$
\frac {m+m'}{n+n'} - \frac {m'} {n'} < 0
$$
这同时也说明，分数 $a/b$ 至多出现一次。
不遗漏性证明
接下来，我们要证明 $\forall a/b \in \mathbb Q^+$，$a/b$ 至少出现一次。
构造下面的获得方式：
$\forall a/b \in \mathbb Q^+$，$a/b$
$$
\frac m n = \frac 0 1 < \Big ( \frac a b \Big ) < \frac 1 0 = \frac {m'}{n'}
$$
这里，我们用"括号" 来代表我们还没有取到这个数。
如果在某个阶段，我们有：
$$
\frac m n < \Big ( \frac a b \Big ) < \frac {m'}{n'}
$$
我们有三种情况：
(1)
$$
\frac a b = \frac {m+m'}{n+n'}
$$
顺利地获得了目标数，也就是说达成了目标。构造终止。
(2)
$$
\frac a b > \frac {m+m'}{n+n'}
$$
我们做如下操作
$$
m \leftarrow m + m'
$$
$$
n \leftarrow n + n'
$$
然后就可以继续进行迭代。因为：
$$
\frac {m+m'}{n+n'} < \frac a b < \frac {m'} {n'}
$$
(3)
$$
\frac a b < \frac {m+m'}{n+n'}
$$
我们做如下操作
$$
m' \leftarrow m + m'
$$
$$
n' \leftarrow n + n'
$$
然后就可以继续进行迭代。因为：
$$
\frac m n < \frac a b < \frac {m+m'}{n+n'}
$$
这个迭代的次数是有限的。因为条件
$$
\begin{aligned}
&~\frac a b - \frac m n > 0, \frac {m'}{n'} - \frac a b < 0 \\
\Leftrightarrow &~ an-mb \geq 1, bm'-an' \geq 1 \\
\Leftrightarrow &~ (m'+n')(an-mb) \geq m'+n',\\
&~(m+n)(bm'-an') \geq m+n \\
\Leftrightarrow &~ (m'+n')(an-mb) + (m+n)(bm'-an') \\
&~ \geq m'+n'+m+n \\
\Leftrightarrow &~ a+b \geq m'+n'+m+n
\end{aligned}
$$
由于 $m, n, m', n'$ 一直递增，所以，我们一定能够在有限步骤内得到 $a/b$。
接下来是关于不遗漏性的讨论：
- 有没有可能 $a/b$ 逃出了框定的界限？不可能。因为最初我们设定了上界和下界：$1/0$, $0/1$。在之后的构造中，$a/b$ 的范围被不断缩小，直至相等。
- 在明确了我们的构造方式不会产生错误情况后，我们论证了构造将会在有限步骤内结束，也就说明了对于任意的 $a/b$ 我们都能够在有限步骤内被成功得到，也就是说$\forall a/b \in \mathbb Q^+$，$a/b$ 至少出现一次。
其实，这个寻找过程就是一种分治，只不过不是均等的二分罢了。我们在构造过程中保证了单调性，同时也论证了步骤的有限性，所以我们就能论证没有数会被遗漏。
后记
感谢 @fcx 提出的疑问。
我们一定要意识到：
$$
a+b = m'+n'+m+n
$$
并不意味着收敛，甚至说这个等式本身就没有什么意义！
回过头看我们是怎么得到不等式的，我们是通过一个严格不等号得到的不等式，然后再通过整数的限制加上了一个大于等于号，所以这个等于号其实并没有什么实际的意义，只是代数变换中的副产物。
再来想想我们证明了什么：
- 能够迭代代表一定符合区间条件，一定满足成立的条件
- 不能继续迭代说明一定达到了目标
- 迭代的次数是有限步
由此便说明了不遗漏。
此外，如果 $a,b$ 不互素，也不会产生问题。因为我们看的是 $a/b$ 这个整体，并没有分开看待 $a,b$。
