为什么要正则化?
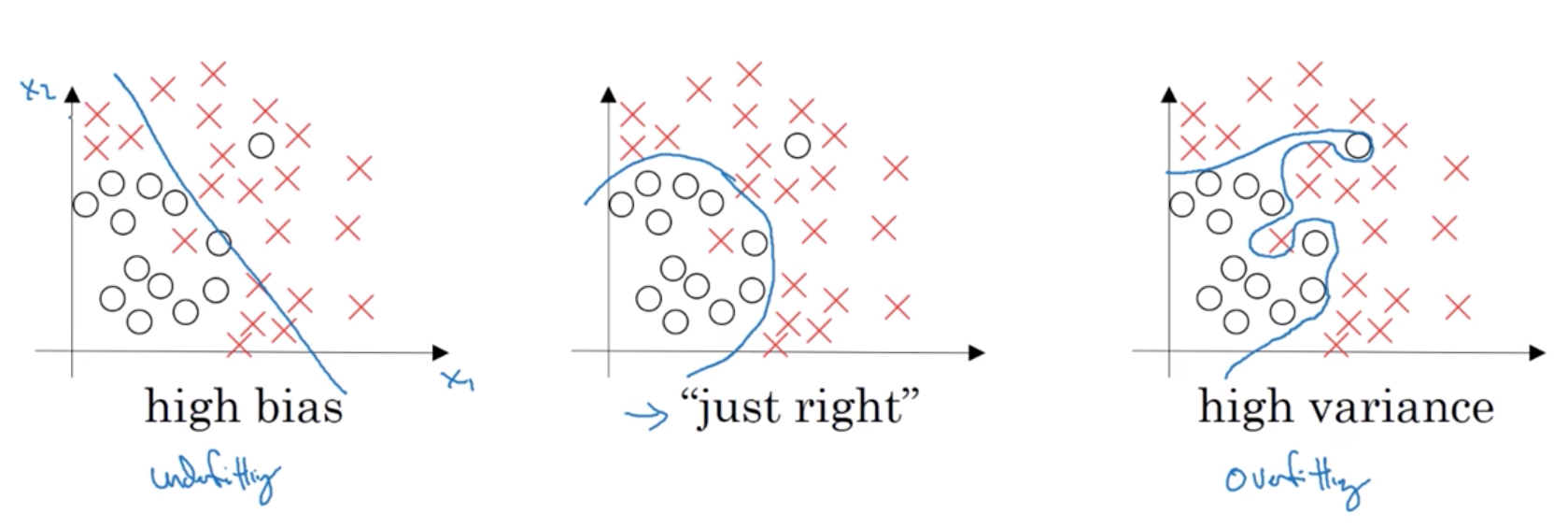
在探讨这个问题之前,我们需要先引入欠拟合和过拟合的概念。
- 左侧:欠拟合,high bias, $error_{train} \gg error_{dev}$
- 右侧:过拟合,high variance, $error_{train} \rightarrow 0\%$
在过拟合的时候我们需要引入正则化,来避免过拟合。
这里介绍两种正则化方式:
- 权重衰减 (weight decay)
- Dropout
Weight Decay
Weight Decay 的主要思想就是加快参数的更新幅度,也就是说增大损失函数,使得梯度下降的步幅变大。但为什么这样可以防止过拟合?根据奥卡姆剃刀法则,我们倾向于认为,参数越小,网络越不复杂,越不容易过拟合,而实践也证明了这一点。
下面的公式节选自我之前的汇报笔记:
- 逻辑回归: $\min_{w, b}J(w, b), w\in \mathbb R^{n_x}, b\in \mathbb R$
- L2 正则化:重定义 $J(w, b)$
$$
J(w, b) = \frac{1}{m}\sum_{i = 1}^{m}\mathcal L(\hat y^{(i)}, y^{(i)}) + \frac{\lambda}{2m}||w||_2^2,~||w||_2^2 = \sum_{j = 1}^{n_x}w_j^2 = w^\mathrm T w
$$ - L1 正则化:重定义 $J(w, b)$
$$
J(w, b) = \frac{1}{m}\sum_{i = 1}^{m}\mathcal L(\hat y^{(i)}, y^{(i)}) + \frac{\lambda}{2m}||w||_1,~||w||_1 = \sum_{j = 1}^{n_x} |w_j|
$$
- L2 正则化:重定义 $J(w, b)$
- 神经网络:重定义损失函数:
$$
J(W^{[1]}, b^{[1]},\cdots, W^{[l]}, b^{[l]}) = \frac{1}{m}\sum_{i = 1}^m \mathcal L(\hat y^{(i)}, y^{(i)}) + \frac{\lambda}{2m}\sum_{i = 1}^m ||W^{[l]}||_\mathrm F^2
$$
$$
||W^{[l]}||_\mathrm F^2 = \displaystyle\sum_{i = 1}^{n^{[l]}}\displaystyle\sum_{j=1}^{n^{[l-1]}}(W^{[l]}_{ij})^2
$$
红色的项标出了正则化后迭代中增加的项:
$$
dW^{[l]} = \frac{1}{m} dZ^{[l]} A^{[l-1] T} \color{red}{ + \frac {\lambda}{m}W^{[l]}}
$$
$$
W^{[l]} \leftarrow W^{[l]} - \alpha\frac{1}{m} dZ^{[l]} A^{[l-1] T}\color{red}{ - \alpha \frac {\lambda}{m}W^{[l]}}
$$
下面的公式出自 d2l 教科书,能让我们更好的理解超参数 $\lambda$ 的作用:
对于线性回归的损失函数:
$$
L(\mathbf{w}, b) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2
$$
我们将其重定义为:
$$
J(\mathbf{w}, b) = L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2,
$$
我们来看参数的迭代式发生了什么变化。这是原来的迭代式:
$$
\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}
$$
这是经过 L2 正则化后的迭代式:
$$
\begin{aligned}
\mathbf{w} & \leftarrow \left(1{\color{red}{- \eta\lambda}} \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)
\end{aligned}
$$
Intuitive understanding of L2 Regularization
$$
\lambda \uparrow \Longrightarrow W \downarrow \Longrightarrow \text{ some of the hidden units may loss effect}
$$
$$
\lambda \uparrow \Longrightarrow W \downarrow \Longrightarrow Z = WA + b \downarrow \Longrightarrow \tanh (z) \rightarrow \text {linear} \Longrightarrow \text {simpler network}
$$
$$
\lambda \uparrow \Longrightarrow \text {high variance, overfit} \rightarrow \text{just right} \rightarrow \text {high bias, underfit}
$$
Weight Decay 的代码实现
如果是自己写,那么我们只需要:
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2
l = loss(net(X), y) + lambd * l2_penalty(w)如果使用 pytorch,我们可以更好地定义 optimizer:
trainer = torch.optim.SGD([
{"params": net[0].weight,'weight_decay': wd},
{"params": net[0].bias}], lr=lr)Dropout
另一种正则化,也就是防止过拟合的方法就是 dropout。
下面的内容引用自 d2l 教课书:
在探究泛化性之前,我们先来定义一下什么是一个“好”的预测模型? 我们期待“好”的预测模型能在未知的数据上有很好的表现: 经典泛化理论认为,为了缩小训练和测试性能之间的差距,应该以简单的模型为目标。 简单性以较小维度的形式展现, 我们在 4.4节 讨论线性模型的单项式函数时探讨了这一点。 此外,正如我们在 4.5节 中讨论权重衰减(正则化)时看到的那样, 参数的范数也代表了一种有用的简单性度量。
简单性的另一个角度是平滑性,即函数不应该对其输入的微小变化敏感。 例如,当我们对图像进行分类时,我们预计向像素添加一些随机噪声应该是基本无影响的。 1995年,克里斯托弗·毕晓普证明了 具有输入噪声的训练等价于Tikhonov正则化 [Bishop, 1995]。 这项工作用数学证实了“要求函数光滑”和“要求函数对输入的随机噪声具有适应性”之间的联系。
然后在2014年,斯里瓦斯塔瓦等人 [Srivastava et al., 2014] 就如何将毕晓普的想法应用于网络的内部层提出了一个想法: 在训练过程中,他们建议在计算后续层之前向网络的每一层注入噪声。 因为当训练一个有多层的深层网络时,注入噪声只会在输入-输出映射上增强平滑性。
这个想法被称为暂退法(dropout)。 暂退法在前向传播过程中,计算每一内部层的同时注入噪声,这已经成为训练神经网络的常用技术。 这种方法之所以被称为暂退法,因为我们从表面上看是在训练过程中丢弃(drop out)一些神经元。 在整个训练过程的每一次迭代中,标准暂退法包括在计算下一层之前将当前层中的一些节点置零。
需要说明的是,暂退法的原始论文提到了一个关于有性繁殖的类比: 神经网络过拟合与每一层都依赖于前一层激活值相关,称这种情况为“共适应性”。 作者认为,暂退法会破坏共适应性,就像有性生殖会破坏共适应的基因一样。
那么关键的挑战就是如何注入这种噪声。 一种想法是以一种无偏向(unbiased)的方式注入噪声。 这样在固定住其他层时,每一层的期望值等于没有噪音时的值。
在毕晓普的工作中,他将高斯噪声添加到线性模型的输入中。 在每次训练迭代中,他将从均值为零的分布 $\epsilon \sim \mathcal{N}(0,\sigma^2)$ 采样噪声添加到输入 $\mathbf{x}$, 从而产生扰动点 $\mathbf{x}' = \mathbf{x} + \epsilon$, 期望是 $E[\mathbf{x}'] = \mathbf{x}$。
在标准暂退法正则化中,通过按保留(未丢弃)的节点的分数进行规范化来消除每一层的偏差。 换言之,每个中间值 $h$ 以暂退概率 $p$ 由随机变量 $h'$ 替换,如下所示:
$$
\begin{aligned}
h' = \begin{cases}
0 & \text{ 概率为 } p \\
\frac{h}{1-p} & \text{ 其他情况}
\end{cases}
\end{aligned}
$$
根据此模型的设计,其期望值保持不变,即 $E[h'] = h$。
Dropout 的代码实现
纯手写:
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在本情况中,所有元素都被丢弃
if dropout == 1:
return torch.zeros_like(X)
# 在本情况中,所有元素都被保留
if dropout == 0:
return X
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)pytorch:
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
# 在第一个全连接层之后添加一个dropout层
nn.Dropout(dropout1),
nn.Linear(256, 256),
nn.ReLU(),
# 在第二个全连接层之后添加一个dropout层
nn.Dropout(dropout2),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)注意:对于 pytorch:
net.eval() # 不启用 dropout (这两个 method 还有其他作用)
net.train() # 启用 dropout