题面

https://www.luogu.com.cn/problem/P1364

题解

复杂度 $O(n)$

高赞题解中说带权树的重心。其实关系不是最大，我们直接嗯推方程其实就可以了。

首先定义:

• $sz[u]$ 是以 $u$ 为根的子树大小
• $f[u]$ 是将 $u$ 设置为医院时的总距离

我们不妨以 $1$ 为根。

第一遍 dfs 初始化 $sz$ 与 $f[1]$:

$$
sz[u] = w[u] + \sum_{v} sz[v]
$$

$$
f[1] = \sum_{u} w[u] \times depth[u]
$$

第二遍 dfs 更新贡献，而且是从上往下更新贡献，因为我们首先求出了 $f[1]$ (根的贡献)：

$$
f[v] = f[u] + (sz[1] - sz[v]) - sz[v]
$$

理由：

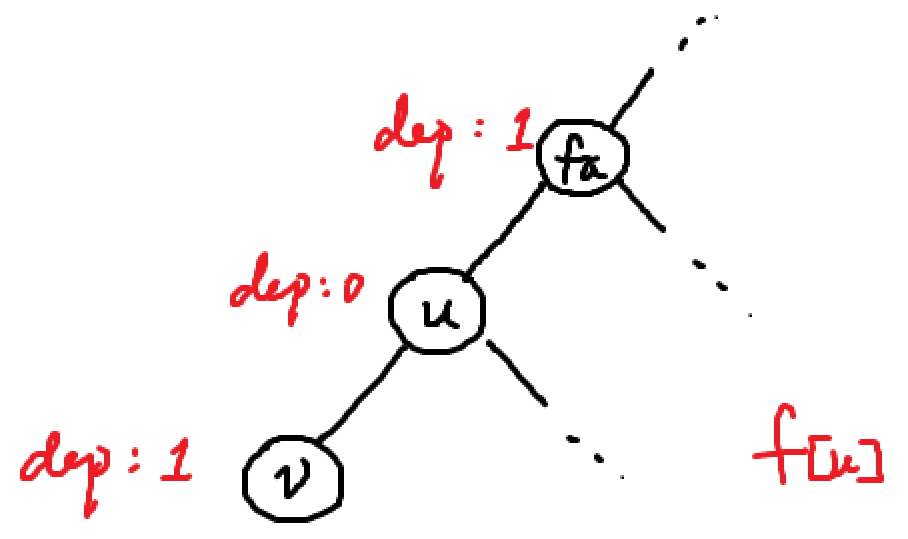
这是 $f[u]$:

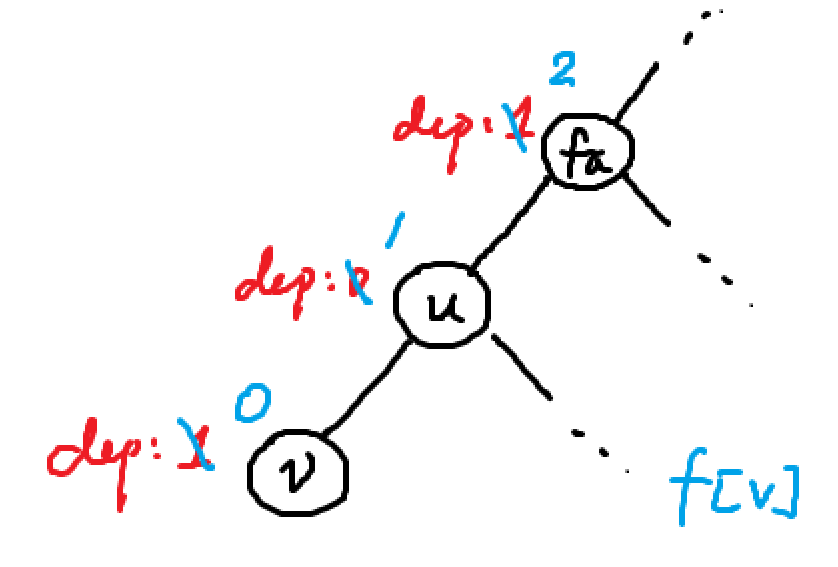
这是 $f[v]$:

也就是说要给 $v$ 以及其子树减去一个贡献，而整棵树除了 $v$ 及其子树的节点都要加上一个贡献，所以就有了

$$

• (sz[1] - sz[v]) - sz[v]
  $$

代码

#include <iostream>

using namespace std;

const int maxn = 1e5;
struct edge { int next, to; } g[maxn << 1];
int head[maxn], w[maxn], f[maxn], sz[maxn], ecnt = 2;
int ans = 2e9+5;

void add_edge(int u, int v) {
    g[ecnt] = (edge) {head[u], v};
    head[u] = ecnt ++;
}

void dfs1(int u, int fa, int dep) {
    sz[u] = w[u];
    for (int e = head[u]; e; e = g[e].next) {
        int v = g[e].to;
        if (v == fa) continue;
        dfs1(v, u, dep + 1);
        sz[u] += sz[v];
    }
    f[1] += w[u] * dep;
}

void dfs2(int u, int fa) {
    for (int e = head[u]; e; e = g[e].next) {
        int v = g[e].to;
        if (v == fa) continue;
        f[v] = f[u] + sz[1] - 2 * sz[v];
        dfs2(v, u);
    }
    ans = min(ans, f[u]);
}

int main() {
    int n; cin >> n;
    for (int i = 1; i <= n; i ++) {
        int ww, u, v; cin >> ww >> u >> v;
        if (u) add_edge(u, i), add_edge(i, u);
        if (v) add_edge(v, i), add_edge(i, v);
        w[i] = ww;
    }
    dfs1(1, 0, 0);
    dfs2(1, 0);
    cout << ans << endl;
    return 0;
}