Dinic 算法
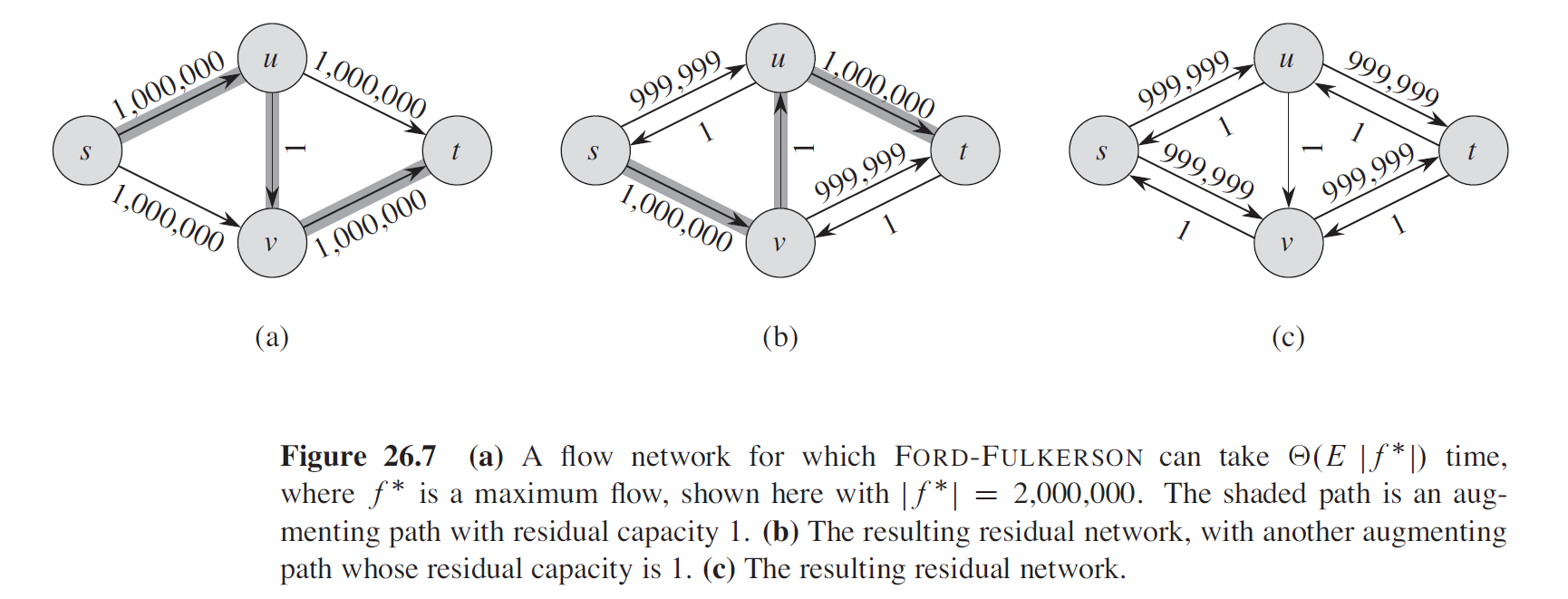
首先我们需要明确:Ford-Fulkerson 的思想是很好的,但是如果直接猛干,这个复杂度暴涨,而且是时候祭出这张经典的图了:
复杂度会飙升到 $O(E\max |f|)$。
那 Dinic 算法做了什么呢?
- 多路增广:找增广路时进行 DFS,这就意味着,如果找到了一条增广路但是流量却还没有被用完,那就用剩余的流量再找一条!
- 最短增广:每次先用 BFS 做分层,算出每个点的距离。在进行 DFS 的时候,我们每次只让深度加一,这样就能以找到最短的增广路。
- 当前弧优化:如果在 DFS 搜索的过程中,我们已经明确某个点顺着残余网络的顺序已经与汇点不再连通,那么就没必要在下次继续搜索,可以在本轮搜索中直接判定为不可达(通过标记距离数组)。
上面听着很玄乎,结合下面的算法流程和代码一起看就能理解了:
$$
\begin {aligned}
&\text{DINIC}(G,s,t) \\
&1~~~~\mathbf{for}\text{ each edge }(u,v)\in G.E \\
&2~~~~~~~~~~~~(u,v).f = 0\\
&3~~~~\mathbf{while }\text{ BFS()} \\
&4~~~~~~~~~~~~\text{ans }= \text{ ans }+ \text{DFS(}s,\infty) \\
&5~~~~\mathbf{return }\text{ ans}
\end {aligned}
$$
Dinic 正确性的讨论
Q: 最短增广,可能会找不到增广路吗?
A: 不可能!因为 BFS 分层时就保证了在残差网络中,源点到汇点是可达的,所以一定有最短增广路存在!
用到的一些 Tricks
- 异或找相反边
- 图直接存的就是残差网络(可以这样做的原因:在最开始,残差网络就等于原网络)
代码
测试传送门: https://www.luogu.com.cn/problem/P3376
#include <iostream>
#include <cstring>
#include <queue>
#define int long long
using namespace std;
const int maxn = 2e2+5;
const int maxm = 5e3+5;
const int inf = 9e18;
queue<int> q;
int head[maxn], d[maxn], ecnt = 2, s, t, n, m;
struct edge { int to, next, w; } g[maxm << 1];
void add_edge(int u, int v, int w) {
g[ecnt] = edge {v, head[u], w};
head[u] = ecnt ++;
}
void add_edge_res(int u, int v, int w) {
add_edge(u, v, w);
add_edge(v, u, 0);
}
// 分层、判断残存网路是否仍然连通
bool bfs() {
memset(d, 0, sizeof(d));
d[s] = 1;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int e = head[u]; e; e = g[e].next) {
int v = g[e].to;
if (d[v] || !g[e].w) continue;
d[v] = d[u] + 1;
q.push(v);
}
}
return d[t];
}
int dfs(int u, int in) {
if (u == t) return in;
int out = 0;
// 多路增广
for (int e = head[u]; e; e = g[e].next) {
int v = g[e].to;
if (d[v] != d[u] + 1 || !g[e].w) continue;
// 递归
int res = dfs(v, min(in, g[e].w));
if (!res) continue;
// 更新输入输出
in -= res;
out += res;
// 更新残存网络
g[e].w -= res;
g[e ^ 1].w += res;
// 剪枝
if (!in) break;
}
// 当前弧优化
if (!out) d[u] = 0;
return out;
}
signed main() {
cin >> n >> m >> s >> t;
int u, v, w;
while (m --> 0) {
cin >> u >> v >> w;
add_edge_res(u, v, w);
}
int ans = 0;
while (bfs())
ans += dfs(s, inf);
cout << ans << endl;
return 0;
}