今天起正式进入高三了。为了夯实基础，遂决定每天刷一题，~~希望别放弃~~。我记得去年这个时候也干过同样的事情，那今天就文艺复兴一下吧，写归并排序。~~虽然我是看着去年的代码写的~~。

归并排序

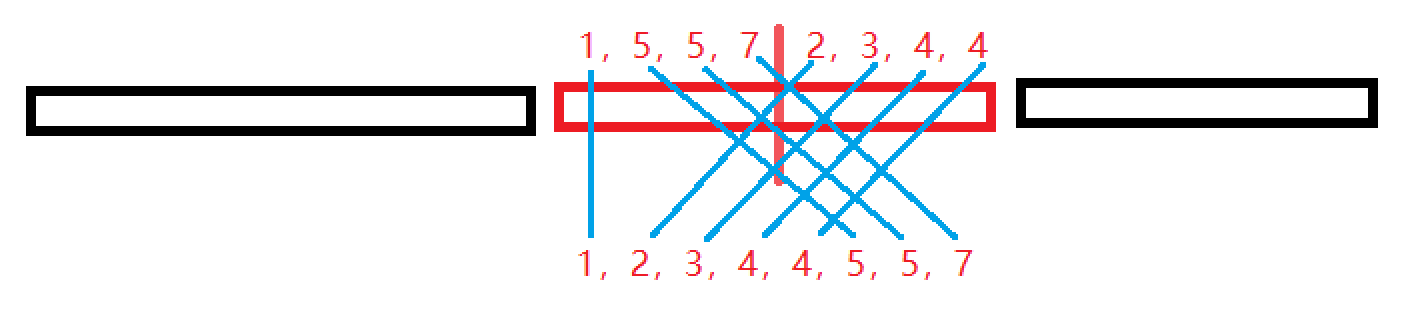
看下图的 Merge

使用分治的思想
主要分为三个步骤
- 将数列对半分
- 递归对子数列排序
- 合并两个子数列

重点肯定在于如何正确地合并两个子序列。双指针线性扫一遍即可，必定有一个先被扫完，然后直接添加没被扫完的子序列剩下的元素（注意：递归，子序列都是有序的）

注意：过程中使用了临时数组存数据，在每次递归最后再拷贝回原数组，这样不会破坏原数据。

代码：

#include <iostream>
#include <cstdio> 

#define int long long

using namespace std;

const int maxn = 1e5 + 5;
int n, a[maxn], t[maxn];

void merge_sort(int l, int r) {
    // [l, r) 左闭右开
    if (r - l <= 1) return;
    int mid = (l + r) >> 1;

    merge_sort(l, mid);
    merge_sort(mid, r);

    int i = l, j = mid, head = l;
    while (i < mid && j < r)
        t[head ++] = a[i] < a[j] ? a[i ++] : a[j ++];
    while (i < mid)
        t[head ++] = a[i ++];
    while (j < r)
        t[head ++] = a[j ++];
    for (int i = l; i < r; i ++)
        a[i] = t[i];
}

signed main() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    merge_sort(1, n + 1);
    for (int i = 1; i <= n; i ++)
        cout << a[i] << (i == n ? '\n' : ' ');
    return 0;
}

测试传送门：P1177 【模板】快速排序

使用归并排序求逆序对的思想

使用归并排序的方法求逆序对，只需要在每次合并时:

如果有后半段的元素在双指针没扫完之前被添加进了临时数组，那么此时前半段还没有被添加进临时数组的数的个数就是这个被添加进去的后半段的元素贡献的在这个处理区间内的逆序对数量。

拿上图举例子：

后半段的 2 被第二个放进临时数组，此时，前半段 5 5 7 还没被放进临时数组，那么 2 在这个处理区间内贡献的逆序对数量就是 3
Q: 为什么排序后对逆序对数量不会发生变化？
A: 我们在对某一段排序时，计算了那一段的逆序对数量。而某一段的位置改变，不会影响那一段和那一段之前或那一段之后的逆序对数量，只影响那一段中的逆序对数量，而他们已经被我们计算了。

对于上面说的内容，我们不妨来证明一下：

整个数列的逆序对数量定义为：

$$
\sum _ {1 \leq i < j \leq n} a_i > a_j
$$

定义区间 $[l, r)$ 为我们正在处理的区间。$[1, l)$ 与 $[l, r)$ 间的逆序对可以记为：

$$
\sum _ {1 \leq i < l, l \leq j < r} a_i > a_j
$$

同理，$[l, r)$ 与 $[r, n]$ 间的逆序对可以记为：

$$
\sum _ {l \leq i < r, r \leq j \leq n} a_i > a_j
$$

可以发现，上述两个逆序对数量与 $[l, r)$ 的子序列排序无关，至于 $[l, r)$ 内的元素有关。

稍微改写一下上面的代码来求逆序对：

int i = l, j = mid, head = l;
while (i < mid && j < r)
    if (a[i] > a[j]) {
        t[head ++] = a[j ++];
        ans += mid - i; // 就是这句在进行计数。之所以不 +1 是因为我们是左闭右开区间
    } else {
        t[head ++] = a[i ++];
    }
while (i < mid)
    t[head ++] = a[i ++];
while (j < r)
    t[head ++] = a[j ++];